
Perturbation theory (quantum mechanics)
Encyclopedia
In quantum mechanics
, perturbation theory is a set of approximation schemes directly related to mathematical perturbation
for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian
representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system (e.g. its energy
levels and eigenstates) can, from considerations of continuity, be expressed as 'corrections' to those of the simple system. These corrections, being 'small' compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. The complicated system can therefore be studied based on knowledge of the simpler one.
for Hamiltonians
of even moderate complexity. The Hamiltonians to which we know exact solutions, such as the hydrogen atom
, the quantum harmonic oscillator
and the particle in a box
, are too idealized to adequately describe most systems. Using perturbation theory, we can use the known solutions of these simple Hamiltonians to generate solutions for a range of more complicated systems. For example, by adding a perturbative electric potential
to the quantum mechanical model of the hydrogen atom, we can calculate the tiny shifts in the spectral line
s of hydrogen caused by the presence of an electric field
(the Stark effect
). This is only approximate because the sum of a Coulomb potential with a linear potential is unstable although the tunneling time (decay rate) is very long. This shows up as a broadening of the energy spectrum lines, something which perturbation theory fails to reproduce entirely.
The expressions produced by perturbation theory are not exact, but they can
lead to accurate results as long as the expansion parameter, say , is very small. Typically, the results are expressed in terms of finite power series in
, is very small. Typically, the results are expressed in terms of finite power series in
 that seem to converge to the exact values when summed to higher order. After a certain order
that seem to converge to the exact values when summed to higher order. After a certain order 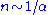 , however, the results become increasingly worse since the series are usually divergent
, however, the results become increasingly worse since the series are usually divergent
(being asymptotic series). There exist ways to convert them into convergent series, which can be evaluated for large-expansion parameters, most efficiently by Variational method
.
In the theory of quantum electrodynamics
(QED), in which the electron
-photon
interaction is treated perturbatively, the calculation of the electron's magnetic moment
has been found to agree with experiment to eleven decimal places. In QED and other quantum field theories
, special calculation techniques known as Feynman diagram
s are used to systematically sum the power series terms.
Under some circumstances, perturbation theory is an invalid approach to take. This happens when the system we wish to describe cannot be described by a small perturbation imposed on some simple system. In quantum chromodynamics
, for instance, the interaction of quark
s with the gluon
field cannot be treated perturbatively at low energies because the coupling constant
(the expansion parameter) becomes too large. Perturbation theory also fails to describe states that are not generated adiabatically from the "free model", including bound state
s and various collective phenomena such as soliton
s. Imagine, for example, that we have a system of free (i.e. non-interacting) particles, to which an attractive interaction is introduced. Depending on the form of the interaction, this may create an entirely new set of eigenstates corresponding to groups of particles bound to one another. An example of this phenomenon may be found in conventional superconductivity
, in which the phonon
-mediated attraction between conduction electrons leads to the formation of correlated electron pairs known as Cooper pair
s. When faced with such systems, one usually turns to other approximation schemes, such as the variational method
and the WKB approximation
. This is because there is no analogue of a bound particle in the unperturbed model and the energy of a soliton typically goes as the inverse of the expansion parameter. However, if we "integrate" over the solitonic phenomena, the nonperturbative corrections in this case will be tiny; of the order of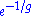 or
or 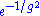 in the perturbation parameter g. Perturbation theory can only detect solutions "close" to the unperturbed solution, even if there are other solutions (which typically blow up as the expansion parameter goes to zero).
in the perturbation parameter g. Perturbation theory can only detect solutions "close" to the unperturbed solution, even if there are other solutions (which typically blow up as the expansion parameter goes to zero).
The problem of non-perturbative systems has been somewhat alleviated by the advent of modern computer
s. It has become practical to obtain numerical non-perturbative solutions for certain problems, using methods such as density functional theory
. These advances have been of particular benefit to the field of quantum chemistry
. Computers have also been used to carry out perturbation theory calculations to extraordinarily high levels of precision, which has proven important in particle physics
for generating theoretical results that can be compared with experiment.
in a 1926 paper, shortly after he produced his theories in wave mechanics. In this paper Schrödinger referred to earlier work of Lord Rayleigh, who investigated harmonic vibrations of a string perturbed by small inhomogeneities. This is why this perturbation theory is often referred to as Rayleigh-Schrödinger perturbation theory.
:
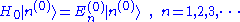
For simplicity, we have assumed that the energies are discrete. The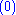 superscripts denote that these quantities are associated with the unperturbed system. Note the use of Bra-ket notation
superscripts denote that these quantities are associated with the unperturbed system. Note the use of Bra-ket notation
.
We now introduce a perturbation to the Hamiltonian. Let V be a Hamiltonian representing a weak physical disturbance, such as a potential energy produced by an external field. (Thus, V is formally a Hermitian operator.) Let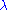 be a dimensionless parameter that can take on values ranging continuously from 0 (no perturbation) to 1 (the full perturbation). The perturbed Hamiltonian is
be a dimensionless parameter that can take on values ranging continuously from 0 (no perturbation) to 1 (the full perturbation). The perturbed Hamiltonian is
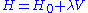
The energy levels and eigenstates of the perturbed Hamiltonian are again given by the Schrödinger equation:

Our goal is to express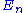 and |n> in terms of the energy levels and eigenstates of the old Hamiltonian. If the perturbation is sufficiently weak, we can write them as power series in λ:
and |n> in terms of the energy levels and eigenstates of the old Hamiltonian. If the perturbation is sufficiently weak, we can write them as power series in λ:

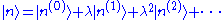
where
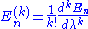
and
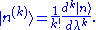
When λ = 0, these reduce to the unperturbed values, which are the first term in each series. Since the perturbation is weak, the energy levels and eigenstates should not deviate too much from their unperturbed values, and the terms should rapidly become smaller as we go to higher order.
Plugging the power series into the Schrödinger equation, we obtain

Expanding this equation and comparing coefficients of each power of λ results in an infinite series of simultaneous equations. The zeroth-order equation is simply the Schrödinger equation for the unperturbed system. The first-order equation is
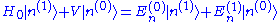
Operating through by <n(0)|. The first term on the left-hand side cancels with the first term on the right-hand side. (Recall, the unperturbed Hamiltonian is hermitian
). This leads to the first-order energy shift:
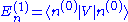
This is simply the expectation value
of the perturbation Hamiltonian while the system is in the unperturbed state. This result can be interpreted in the following way: suppose the perturbation is applied, but we keep the system in the quantum state |n(0)>, which is a valid quantum state though no longer an energy eigenstate. The perturbation causes the average energy of this state to increase by <n(0)|V|n(0)>. However, the true energy shift is slightly different, because the perturbed eigenstate is not exactly the same as |n(0)>. These further shifts are given by the second and higher order corrections to the energy.
Before we compute the corrections to the energy eigenstate, we need to address the issue of normalization. We may suppose <n(0)|n(0)>=1, but perturbation theory assumes we also have <n|n>=1. It follows that at first order in λ, we must have <n(0)|n(1)>+<n(1)|n(0)>=0. Since the overall phase is not determined in quantum mechanics, without loss of generality, we may assume <n(0)|n> is purely real. Therefore, <n(0)|n(1)>=-<n(1)|n(0)>, and we deduce
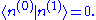
To obtain the first-order correction to the energy eigenstate, we insert our expression for the first-order energy correction back into the result shown above of equating the first-order coefficients of λ. We then make use of the resolution of the identity,
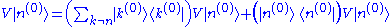
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, perturbation theory is a set of approximation schemes directly related to mathematical perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system (e.g. its energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
levels and eigenstates) can, from considerations of continuity, be expressed as 'corrections' to those of the simple system. These corrections, being 'small' compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. The complicated system can therefore be studied based on knowledge of the simpler one.
Applications of perturbation theory
Perturbation theory is an important tool for describing real quantum systems, as it turns out to be very difficult to find exact solutions to the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for Hamiltonians
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of even moderate complexity. The Hamiltonians to which we know exact solutions, such as the hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
, the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
and the particle in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
, are too idealized to adequately describe most systems. Using perturbation theory, we can use the known solutions of these simple Hamiltonians to generate solutions for a range of more complicated systems. For example, by adding a perturbative electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
to the quantum mechanical model of the hydrogen atom, we can calculate the tiny shifts in the spectral line
Spectral line
A spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
s of hydrogen caused by the presence of an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
(the Stark effect
Stark effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
). This is only approximate because the sum of a Coulomb potential with a linear potential is unstable although the tunneling time (decay rate) is very long. This shows up as a broadening of the energy spectrum lines, something which perturbation theory fails to reproduce entirely.
The expressions produced by perturbation theory are not exact, but they can
lead to accurate results as long as the expansion parameter, say
 , is very small. Typically, the results are expressed in terms of finite power series in
, is very small. Typically, the results are expressed in terms of finite power series in that seem to converge to the exact values when summed to higher order. After a certain order
that seem to converge to the exact values when summed to higher order. After a certain order  , however, the results become increasingly worse since the series are usually divergent
, however, the results become increasingly worse since the series are usually divergentDivergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
(being asymptotic series). There exist ways to convert them into convergent series, which can be evaluated for large-expansion parameters, most efficiently by Variational method
Variational method (quantum mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states...
.
In the theory of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
(QED), in which the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
-photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
interaction is treated perturbatively, the calculation of the electron's magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
has been found to agree with experiment to eleven decimal places. In QED and other quantum field theories
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, special calculation techniques known as Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s are used to systematically sum the power series terms.
Under some circumstances, perturbation theory is an invalid approach to take. This happens when the system we wish to describe cannot be described by a small perturbation imposed on some simple system. In quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, for instance, the interaction of quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s with the gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
field cannot be treated perturbatively at low energies because the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
(the expansion parameter) becomes too large. Perturbation theory also fails to describe states that are not generated adiabatically from the "free model", including bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
s and various collective phenomena such as soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s. Imagine, for example, that we have a system of free (i.e. non-interacting) particles, to which an attractive interaction is introduced. Depending on the form of the interaction, this may create an entirely new set of eigenstates corresponding to groups of particles bound to one another. An example of this phenomenon may be found in conventional superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, in which the phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
-mediated attraction between conduction electrons leads to the formation of correlated electron pairs known as Cooper pair
Cooper pair
In condensed matter physics, a Cooper pair or BCS pair is two electrons that are bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper...
s. When faced with such systems, one usually turns to other approximation schemes, such as the variational method
Variational method (quantum mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states...
and the WKB approximation
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
. This is because there is no analogue of a bound particle in the unperturbed model and the energy of a soliton typically goes as the inverse of the expansion parameter. However, if we "integrate" over the solitonic phenomena, the nonperturbative corrections in this case will be tiny; of the order of
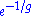 or
or 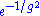 in the perturbation parameter g. Perturbation theory can only detect solutions "close" to the unperturbed solution, even if there are other solutions (which typically blow up as the expansion parameter goes to zero).
in the perturbation parameter g. Perturbation theory can only detect solutions "close" to the unperturbed solution, even if there are other solutions (which typically blow up as the expansion parameter goes to zero).The problem of non-perturbative systems has been somewhat alleviated by the advent of modern computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s. It has become practical to obtain numerical non-perturbative solutions for certain problems, using methods such as density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
. These advances have been of particular benefit to the field of quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
. Computers have also been used to carry out perturbation theory calculations to extraordinarily high levels of precision, which has proven important in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
for generating theoretical results that can be compared with experiment.
Time-independent perturbation theory
Time-independent perturbation theory is one of two categories of perturbation theory, the other being time-dependent perturbation (see next section). In time-independent perturbation theory the perturbation Hamiltonian is static (i.e., possesses no time dependence). Time-independent perturbation theory was presented by Erwin SchrödingerErwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
in a 1926 paper, shortly after he produced his theories in wave mechanics. In this paper Schrödinger referred to earlier work of Lord Rayleigh, who investigated harmonic vibrations of a string perturbed by small inhomogeneities. This is why this perturbation theory is often referred to as Rayleigh-Schrödinger perturbation theory.
First order corrections
We begin with an unperturbed Hamiltonian H0, which is also assumed to have no time dependence. It has known energy levels and eigenstates, arising from the time-independent Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
:
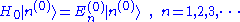
For simplicity, we have assumed that the energies are discrete. The
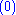 superscripts denote that these quantities are associated with the unperturbed system. Note the use of Bra-ket notation
superscripts denote that these quantities are associated with the unperturbed system. Note the use of Bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
.
We now introduce a perturbation to the Hamiltonian. Let V be a Hamiltonian representing a weak physical disturbance, such as a potential energy produced by an external field. (Thus, V is formally a Hermitian operator.) Let
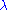 be a dimensionless parameter that can take on values ranging continuously from 0 (no perturbation) to 1 (the full perturbation). The perturbed Hamiltonian is
be a dimensionless parameter that can take on values ranging continuously from 0 (no perturbation) to 1 (the full perturbation). The perturbed Hamiltonian is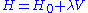
The energy levels and eigenstates of the perturbed Hamiltonian are again given by the Schrödinger equation:

Our goal is to express
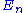 and |n> in terms of the energy levels and eigenstates of the old Hamiltonian. If the perturbation is sufficiently weak, we can write them as power series in λ:
and |n> in terms of the energy levels and eigenstates of the old Hamiltonian. If the perturbation is sufficiently weak, we can write them as power series in λ:
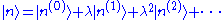
where
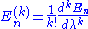
and
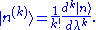
When λ = 0, these reduce to the unperturbed values, which are the first term in each series. Since the perturbation is weak, the energy levels and eigenstates should not deviate too much from their unperturbed values, and the terms should rapidly become smaller as we go to higher order.
Plugging the power series into the Schrödinger equation, we obtain

Expanding this equation and comparing coefficients of each power of λ results in an infinite series of simultaneous equations. The zeroth-order equation is simply the Schrödinger equation for the unperturbed system. The first-order equation is
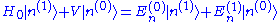
Operating through by <n(0)|. The first term on the left-hand side cancels with the first term on the right-hand side. (Recall, the unperturbed Hamiltonian is hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
). This leads to the first-order energy shift:
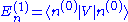
This is simply the expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
of the perturbation Hamiltonian while the system is in the unperturbed state. This result can be interpreted in the following way: suppose the perturbation is applied, but we keep the system in the quantum state |n(0)>, which is a valid quantum state though no longer an energy eigenstate. The perturbation causes the average energy of this state to increase by <n(0)|V|n(0)>. However, the true energy shift is slightly different, because the perturbed eigenstate is not exactly the same as |n(0)>. These further shifts are given by the second and higher order corrections to the energy.
Before we compute the corrections to the energy eigenstate, we need to address the issue of normalization. We may suppose <n(0)|n(0)>=1, but perturbation theory assumes we also have <n|n>=1. It follows that at first order in λ, we must have <n(0)|n(1)>+<n(1)|n(0)>=0. Since the overall phase is not determined in quantum mechanics, without loss of generality, we may assume <n(0)|n> is purely real. Therefore, <n(0)|n(1)>=-<n(1)|n(0)>, and we deduce
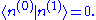
To obtain the first-order correction to the energy eigenstate, we insert our expression for the first-order energy correction back into the result shown above of equating the first-order coefficients of λ. We then make use of the resolution of the identity,
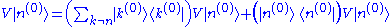
-
-

where is in the orthogonal complement of
is in the orthogonal complement of 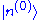 . The result is
. The result is

For the moment, suppose that the zeroth-order energy level is not degenerateDegenerate energy levelIn physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
, i.e. there is no eigenstate of in the orthogonal complement of
in the orthogonal complement of 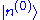 with the energy
with the energy 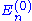 . We multiply through by <k(0)|, which gives
. We multiply through by <k(0)|, which gives
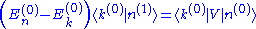
and hence the component of the first-order correction along |k(0)> since by assumption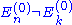 . In total we get
. In total we get

The first-order change in the n-th energy eigenket has a contribution from each of the energy eigenstates k ≠ n. Each term is proportional to the matrix element <k(0)|V|n(0)>, which is a measure of how much the perturbation mixes eigenstate n with eigenstate k; it is also inversely proportional to the energy difference between eigenstates k and n, which means that the perturbation deforms the eigenstate to a greater extent if there are more eigenstates at nearby energies. We see also that the expression is singular if any of these states have the same energy as state n, which is why we assumed that there is no degeneracy.
Second-order and higher corrections
We can find the higher-order deviations by a similar procedure, though the calculations become quite tedious with our current formulation. Our normalization prescription gives that 2<n(0)|n(2)>+<n(1)|n(1)>=0. Up to second order, the expressions for the energies and (normalized) eigenstates are:
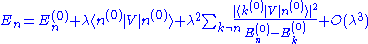

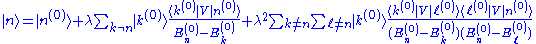
Extending the process further, the third-order energy correction can be shown to be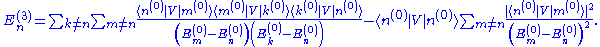
Effects of degeneracy
Suppose that two or more energy eigenstates are degenerateDegenerate energy levelIn physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
. The first-order energy shift is not well defined, since there is no unique way to choose a basis of eigenstates for the unperturbed system. The calculation of the change in the eigenstate is problematic as well, because the operator
does not have a well-defined inverse.
Let D denote the subspace spanned by these degenerate eigenstates. No matter how small the perturbation is, in the degenerate subspace D the energy differences between the eigenstates are zero, so complete mixing of at least some of these states is assured. Thus the perturbation can not be considered small in the D subspace and in that subspace the new Hamiltonian must be diagonalized first. These correct perturbed eigenstates in D are now the basis for the perturbation expansion:
are zero, so complete mixing of at least some of these states is assured. Thus the perturbation can not be considered small in the D subspace and in that subspace the new Hamiltonian must be diagonalized first. These correct perturbed eigenstates in D are now the basis for the perturbation expansion: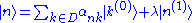
where only eigenstates outside of the D subspace are considered to be small. For the first-order perturbation we need to solve the perturbed Hamiltonian restricted to the degenerate subspace D
simultaneously for all the degenerate eigenstates, where are first-order corrections to the degenerate energy levels. This is equivalent to diagonalizing the matrix
are first-order corrections to the degenerate energy levels. This is equivalent to diagonalizing the matrix
This procedure is approximate, since we neglected states outside the D subspace. The splitting of degenerate energies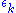 is generally observed. Although the splitting may be small compared to the range of energies found in the system, it is crucial in understanding certain details, such as spectral lines in Electron Spin Resonance experiments.
is generally observed. Although the splitting may be small compared to the range of energies found in the system, it is crucial in understanding certain details, such as spectral lines in Electron Spin Resonance experiments.
Higher-order corrections due to other eigenstates can be found in the same way as for the non-degenerate case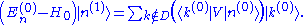
The operator on the left hand side is not singular when applied to eigenstates outside D, so we can write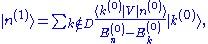
but the effect on the degenerate states is minuscule, proportional to the square of the first-order correction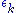 .
.
Near-degenerate states should also be treated in the above manner, since the original Hamiltonian won't be larger than the perturbation in the near-degenerate subspace. An application is found in the nearly-free electron modelNearly-free electron modelIn solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
, where near-degeneracy treated properly gives rise to an energy gap even for small perturbations. Other eigenstates will only shift the absolute energy of all near-degenerate states simultaneously.
Generalization to Multi-parameter Case
The generalization of the time-independent perturbation theory to the multi-parameter case can be formulated more systematically using the language of differential geometry, which basically defines the derivatives of the quantum states and calculate the perturbative corrections by taking derivatives iteratively at the unperturbed point.
Hamiltonian and Force Operator
From the differential geometric point of view, a parameterized Hamiltonian is considered as a function defined on the parameter manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
that maps each particular set of parameters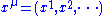 to an Hermitian operator
to an Hermitian operator  that acts on the Hilbert space. The parameters here can be external field, interaction strength, or driving parameters in the quantum phase transitionQuantum phase transitionIn physics, a quantum phase transition is a phase transition between different quantum phases . Contrary to classical phase transitions, quantum phase transitions can only be accessed by varying a physical parameter - such as magnetic field or pressure - at absolute zero temperature...
that acts on the Hilbert space. The parameters here can be external field, interaction strength, or driving parameters in the quantum phase transitionQuantum phase transitionIn physics, a quantum phase transition is a phase transition between different quantum phases . Contrary to classical phase transitions, quantum phase transitions can only be accessed by varying a physical parameter - such as magnetic field or pressure - at absolute zero temperature...
. Let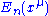 and
and  be the nth eigenenergy and eigenstate of
be the nth eigenenergy and eigenstate of  respectively. In the language of deferential geometry, the states
respectively. In the language of deferential geometry, the states  form a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
form a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over the parameter manifold, on which derivatives of these states can be defined. The perturbation theory is to answer the following question: given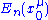 and
and 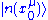 at a unperturbed reference point
at a unperturbed reference point 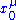 , how to estimate the
, how to estimate the 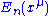 and
and 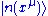 at
at  close to that reference point.
close to that reference point.
With out loss of generality, the coordinate system can be shifted, such that the reference point is set to be the origin. The following linearly parameterized Hamiltonian is frequently used
is set to be the origin. The following linearly parameterized Hamiltonian is frequently used .
.
If the parameters are considered as generalized coordinates, then
are considered as generalized coordinates, then  should be identified as the generalized force operators related to those coordinates. Different indices μ's label the different forces along different directions in the parameter manifold. For example, if
should be identified as the generalized force operators related to those coordinates. Different indices μ's label the different forces along different directions in the parameter manifold. For example, if 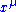 denotes the external magnetic field in the μ-direction, then
denotes the external magnetic field in the μ-direction, then 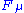 should be the magnetization in the same direction.
should be the magnetization in the same direction.
Perturbation Theory as Power Series Expansion
The validity of the perturbation theory lies on the adiabatic assumption, which assumes the eigenenergies and eigenstates of the Hamiltonian are smooth functions of parameters such that their values in the vicinity region can be calculated in power series (like Taylor expansionTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
) of the parameters: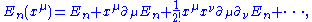

Here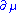 denotes the derivative with respect to
denotes the derivative with respect to 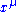 . When applying to the state
. When applying to the state 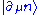 , it should be understood as the Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
, it should be understood as the Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
if the vector bundle is equipped with non-vanishing connectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
. All the terms on the right-hand-side of the series are evaluated at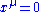 , e.g.
, e.g. 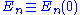 and
and 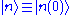 . This convention will be adopted though out the this subsection, that all functions without the parameter dependence explicitly stated are assumed to be evaluated at the origin. The power series may converge slowly or even not converging when the energy levels are close to each other. The adiabatic assumption breaks down when there is energy level degeneracy, and hence the perturbation theory is not applicable in that case.
. This convention will be adopted though out the this subsection, that all functions without the parameter dependence explicitly stated are assumed to be evaluated at the origin. The power series may converge slowly or even not converging when the energy levels are close to each other. The adiabatic assumption breaks down when there is energy level degeneracy, and hence the perturbation theory is not applicable in that case.
Hellmann-Feynman Theorems
The above power series expansion can be readily evaluated if there is a systematic approach to calculate the derivates to any order. Using the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the derivatives can be broken down to the single derivative on either the energy or the state. The Hellmann-Feynman theoremsHellmann-Feynman theoremIn quantum mechanics, the Hellmann–Feynman theorem relates the derivative of the total energy with respect to a parameter, to the expectation value of the derivative of the Hamiltonian with respect to that same parameter...
are used to calculated these single derivatives. The first Hellmann-Feynman theorem gives the derivative of the energy, .
.
The second Hellmann-Feynman theorem gives the derivative of the state (resolved by the complete basis with m ≠ n),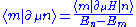 ,
,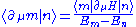 .
.
For the linearly parameterized Hamiltonian,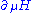 simply stands for the generalized force operator
simply stands for the generalized force operator 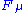 .
.
The theorems can be simply derived by applying the differential operator to both sides of the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
to both sides of the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
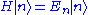 , which reads
, which reads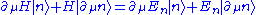 .
.
Then overlap with the state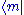 from left and make use of the Schrödinger equation again
from left and make use of the Schrödinger equation again 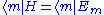 ,
,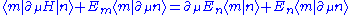 .
.
Given that the eigenstates of the Hamiltonian always from a set of orthonormal basis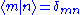 , both the cases of m = n and m ≠ n can be discussed separately. The first case will lead to the first theorem and the second case to the second theorem, which can be shown immediately by rearranging the terms. With the differential rules given by the Hellmann-Feynman theorems, the perturbative correction to the energies and states can be calculated systematically.
, both the cases of m = n and m ≠ n can be discussed separately. The first case will lead to the first theorem and the second case to the second theorem, which can be shown immediately by rearranging the terms. With the differential rules given by the Hellmann-Feynman theorems, the perturbative correction to the energies and states can be calculated systematically.
Correction of Energy and State
To the second order, the energy correction reads .
.
The first order derivative is given by the first Hellmann-Feynman theorem directly. To obtain the second order derivative
is given by the first Hellmann-Feynman theorem directly. To obtain the second order derivative  , simply applying the differential operator
, simply applying the differential operator  to the result of the first order derivative
to the result of the first order derivative 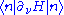 , which reads
, which reads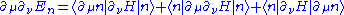 .
.
Note that for linearly parameterized Hamiltonian, there is no second derivative on the operator level. Resolve the derivative of state by inserting the complete set of basis,
on the operator level. Resolve the derivative of state by inserting the complete set of basis,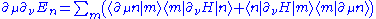 ,
,
then all parts can be calculated using the Hellmann-Feynman theorems. In terms of Lie derivatives,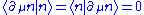 according to the definition of the connection for the vector bundle. Therefore the case m = n can be excluded from the summation, which avoids the singularity of the energy denominator. The same procedure can be carried on for higher order derivatives, from which higher order corrections are obtained.
according to the definition of the connection for the vector bundle. Therefore the case m = n can be excluded from the summation, which avoids the singularity of the energy denominator. The same procedure can be carried on for higher order derivatives, from which higher order corrections are obtained.
The same computational scheme is applicable for the correction of states. The result to the second order is as follows
Both energy derivatives and state derivatives will be involved in deduction. Whenever a state derivative is encountered, resolve it by inserting the complete set of basis, then the Hellmann-Feynman theorem is applicable. Because differentiation can be calculated systematically, the series expansion approach to the perturbative corrections can be coded on computers with symbolic processing softwares like MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
.
Effective Hamiltonian
Let H(0) be the Hamiltonian completely restricted either in the low-energy subspace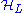 or in the high-energy subspace
or in the high-energy subspace  , such that there is no matrix element in H(0) connecting the low- and the high-energy subspaces, i.e.
, such that there is no matrix element in H(0) connecting the low- and the high-energy subspaces, i.e.  if
if 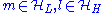 . Let
. Let 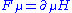 be the coupling terms connecting the subspaces. Then when the high energy degrees of freedoms are integrated out, the effective Hamiltonian in the low energy subspace reads
be the coupling terms connecting the subspaces. Then when the high energy degrees of freedoms are integrated out, the effective Hamiltonian in the low energy subspace reads .
.
Here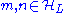 are restricted in the low energy subspace. The above result can be derived by power series expansion of
are restricted in the low energy subspace. The above result can be derived by power series expansion of  .
.
Bold text
Method of variation of constants
Time-dependent perturbation theory, developed by Paul DiracPaul DiracPaul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, studies the effect of a time-dependent perturbation V(t) applied to a time-independent Hamiltonian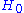 . Since the perturbed Hamiltonian is time-dependent, so are its energy levels and eigenstates. Therefore, the goals of time-dependent perturbation theory are slightly different from time-independent perturbation theory. We are interested in the following quantities:
. Since the perturbed Hamiltonian is time-dependent, so are its energy levels and eigenstates. Therefore, the goals of time-dependent perturbation theory are slightly different from time-independent perturbation theory. We are interested in the following quantities:
- The time-dependent expectation value of some observable A, for a given initial state.
- The time-dependent amplitudes of those quantum states that are energy eigenkets (eigenvectors) in the unperturbed system.
The first quantity is important because it gives rise to the classicalClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
result of an A measurement performed on a macroscopic number of copies of the perturbed system. For example, we could take A to be the displacement in the x-direction of the electron in a hydrogen atom, in which case the expected value, when multiplied by an appropriate coefficient, gives the time-dependent dielectric polarization of a hydrogen gas. With an appropriate choice of perturbation (i.e. an oscillating electric potential), this allows us to calculate the AC permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of the gas.
The second quantity looks at the time-dependent probability of occupation for each eigenstate. This is particularly useful in laserLaserA laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
physics, where one is interested in the populations of different atomic states in a gas when a time-dependent electric field is applied. These probabilities are also useful for calculating the "quantum broadening" of spectral lineSpectral lineA spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
s (see line broadening).
We will briefly examine the ideas behind Dirac's formulation of time-dependent perturbation theory. Choose an energy basis for the unperturbed system. (We will drop the (0) superscripts for the eigenstates, because it is not meaningful to speak of energy levels and eigenstates for the perturbed system.)
for the unperturbed system. (We will drop the (0) superscripts for the eigenstates, because it is not meaningful to speak of energy levels and eigenstates for the perturbed system.)
If the unperturbed system is in eigenstate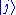 at time
at time  , its state at subsequent times varies only by a phasePhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, its state at subsequent times varies only by a phasePhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
(we are following the Schrödinger pictureSchrödinger pictureIn physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
, where state vectors evolve in time and operators are constant):

We now introduce a time-dependent perturbing Hamiltonian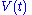 . The Hamiltonian of the perturbed system is
. The Hamiltonian of the perturbed system is

Let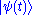 denote the quantum state of the perturbed system at time t. It obeys the time-dependent Schrödinger equation,
denote the quantum state of the perturbed system at time t. It obeys the time-dependent Schrödinger equation,
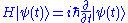
The quantum state at each instant can be expressed as a linear combination of the eigenbasis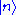 . We can write the linear combination as
. We can write the linear combination as

where the s are undetermined complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s are undetermined complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
functions of t which we will refer to as amplitudes (strictly speaking, they are the amplitudes in the Dirac picture). We have explicitly extracted the exponential phase factors exp(-iEnt/h) on the right hand side. This is only a matter of convention, and may be done without loss of generality. The reason we go to this trouble is that when the system starts in the state |j> and no perturbation is present, the amplitudes have the convenient property that, for all t, cj(t) = 1 and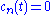 if
if  .
.
The absolute square of the amplitude cn(t) is the probability that the system is in state n at time t, since
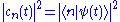
Plugging into the Schrödinger equation and using the fact that ∂/∂t acts by a chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, we obtain

By resolving the identity in front of V, this can be reduced to a set of partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s for the amplitudes:
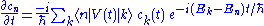
The matrix elements of V play a similar role as in time-independent perturbation theory, being proportional to the rate at which amplitudes are shifted between states. Note, however, that the direction of the shift is modified by the exponential phase factor. Over times much longer than the energy difference Ek-En, the phase winds many times. If the time-dependence of V is sufficiently slow, this may cause the state amplitudes to oscillate. Such oscillations are useful for managing radiative transitions in a laserLaserA laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
.
Up to this point, we have made no approximations, so this set of differential equations is exact. By supplying appropriate initial values cn(0), we could in principle find an exact (i.e. non-perturbative) solution. This is easily done when there are only two energy levels (n = 1, 2), and the solution is useful for modelling systems like the ammoniaAmmoniaAmmonia is a compound of nitrogen and hydrogen with the formula . It is a colourless gas with a characteristic pungent odour. Ammonia contributes significantly to the nutritional needs of terrestrial organisms by serving as a precursor to food and fertilizers. Ammonia, either directly or...
molecule. However, exact solutions are difficult to find when there are many energy levels, and one instead looks for perturbative solutions, which may be obtained by putting the equations in an integral form:
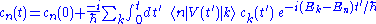
By repeatedly substituting this expression for cn back into right hand side, we get an iterative solution

where, for example, the first-order term is
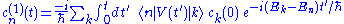
Many further results may be obtained, such as Fermi's golden ruleFermi's golden ruleIn quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
, which relates the rate of transitions between quantum states to the density of states at particular energies, and the Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
, obtained by applying the iterative method to the time evolution operatorHamiltonian (quantum mechanics)In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
, which is one of the starting points for the method of Feynman diagramFeynman diagramFeynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s.
Method of Dyson series
Time dependent perturbations can be treated with the technique of Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
. Taking Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
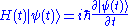
this has the formal solution

being the time ordering operator such that
the time ordering operator such that

if and
and
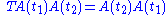
if so that the exponential will represent the following Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
so that the exponential will represent the following Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
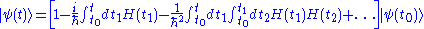 .
.
Now, let us take the following perturbation problem
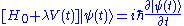
assuming that the parameter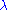 is small and that we are able to solve the problem
is small and that we are able to solve the problem 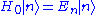 . We do the following unitary transformation going to interaction pictureInteraction pictureIn quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
. We do the following unitary transformation going to interaction pictureInteraction pictureIn quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
or Dirac pictureInteraction pictureIn quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
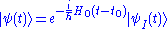
and so the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
becomes
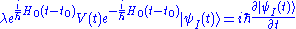
that can be solved through the above Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
as


being this a perturbation series with small . Using the solution of the unperturbed problem
. Using the solution of the unperturbed problem  and
and 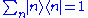 (for the sake of simplicity we assume a pure discrete spectrum), we will have till first order
(for the sake of simplicity we assume a pure discrete spectrum), we will have till first order
 .
.
So, the system, initially in the unperturbed state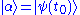 , due to the perturbation can go into the state
, due to the perturbation can go into the state  . The corresponding probability amplitude will be
. The corresponding probability amplitude will be
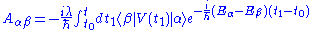
and the corresponding transition probability will be given by Fermi's golden ruleFermi's golden ruleIn quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
.
Time independent perturbation theory can be derived from the time dependent perurbation theory. For this purpose, let us write the unitary evolution operator, obtained from the above Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
, as

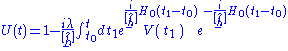
and we take the perturbation time independent. Using the identity
time independent. Using the identity
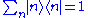
with for a pure discrete spectrum, we can write
for a pure discrete spectrum, we can write
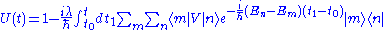

We see that, at second order, we have to sum on all the intermediate states. We assume and the asymptotic limit of larger times. This means that, at each contribution of the perturbation series, we have to add a multiplicative factor
and the asymptotic limit of larger times. This means that, at each contribution of the perturbation series, we have to add a multiplicative factor 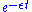 in the integrands so that, the limit
in the integrands so that, the limit  will give back the final state of the system by eliminating all oscillating terms but keeping the secular ones.
will give back the final state of the system by eliminating all oscillating terms but keeping the secular ones.  must be postulated as being arbitrarily small. In this way we can compute the integrals and, separating the diagonal terms from the others, we have
must be postulated as being arbitrarily small. In this way we can compute the integrals and, separating the diagonal terms from the others, we have


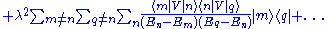
where the time secular series yields the eigenvalues of the perturbed problem and the remaining part gives the corrections to the eigenfunctions. The unitary evolution operator is applied to whatever eigenstate of the unperturbed problem and, in this case, we will get a secular series that holds at small times.
Strong perturbation theory
In a similar way as for small perturbations, it is possible to develop a strong perturbation theory. Let us consider as usual the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

and we consider the question if a dual Dyson series exists that applies in the limit of a perturbation increasingly large. This question can be answered in an affirmative way and the series is the well-known adiabatic series. This approach is quite general and can be shown in the following way. Let us consider the perturbation problem

being . Our aim is to find a solution in the form
. Our aim is to find a solution in the form
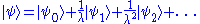
but a direct substitution into the above equation fails to produce useful results. This situation can be adjusted making a rescaling of the time variable as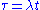 producing the following meaningful equations
producing the following meaningful equations
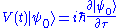
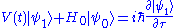

that can be solved once we know the solution of the leading order equation. But we know that in this case we can use the adiabatic approximation. When does not depend on time one gets the Wigner-Kirkwood series that is often used in statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
does not depend on time one gets the Wigner-Kirkwood series that is often used in statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. Indeed, in this case we introduce the unitary transformation
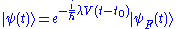
that defines a free picture as we are trying to eliminate the interaction term. Now, in dual way with respect to the small perturbations, we have to solve the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

and we see that the expansion parameter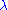 appears only into the exponential and so, the corresponding Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
appears only into the exponential and so, the corresponding Dyson seriesDyson seriesIn scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
, a dual Dyson series, is meaningful at large s and is
s and is
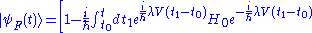

After the rescaling in time we can see that this is indeed a series in
we can see that this is indeed a series in  justifying in this way the name of dual Dyson series. The reason is that we have obtained this series simply interchanging
justifying in this way the name of dual Dyson series. The reason is that we have obtained this series simply interchanging 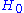 and
and 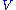 and we can go from one to another applying this exchange. This is called duality principle in perturbation theory. The choice
and we can go from one to another applying this exchange. This is called duality principle in perturbation theory. The choice 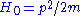 yields, as already said, a Wigner-Kirkwood series that is a gradient expansion. The Wigner-Kirkwood series is a semiclassical series with eigenvalues given exactly as for WKB approximationWKB approximationIn mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
yields, as already said, a Wigner-Kirkwood series that is a gradient expansion. The Wigner-Kirkwood series is a semiclassical series with eigenvalues given exactly as for WKB approximationWKB approximationIn mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
.
-

