Lorentz group
Encyclopedia
In physics
(and mathematics
), the Lorentz group is the group
of all Lorentz transformation
s of Minkowski spacetime, the classical
setting for all (nongravitational) physical phenomena
. The Lorentz group is named for the Dutch
physicist Hendrik Lorentz
.
The mathematical form of
are each invariant under the Lorentz transformation
s. Therefore the Lorentz group is said to express the fundamental symmetry
of many of the known fundamental Laws of Nature.
of the Poincaré group
, the group of all isometries
of Minkowski space-time. The Lorentz transformations are precisely the isometries which leave the origin fixed. Thus, the Lorentz group is an isotropy subgroup of the isometry group of Minkowski spacetime. For this reason, the Lorentz group is sometimes called the homogeneous Lorentz group while the Poincaré group is sometimes called the inhomogeneous Lorentz group. Lorentz transformations are examples of linear transformations; general isometries of Minkowski spacetime are affine transformations.
Mathematically, the Lorentz group may be described as the generalized orthogonal group
O(1,3), the matrix Lie group which preserves the quadratic form
on R4. This quadratic form is interpreted in physics as the metric tensor
of Minkowski spacetime, so this definition is simply a restatement of the fact that Lorentz transformations are precisely the linear transformations which are also isometries of Minkowski spacetime.
The Lorentz group is a six-dimensional
noncompact
real Lie group which is not connected
. All four of its connected components are not simply connected. The identity component
(i.e. the component containing the identity element) of the Lorentz group is itself a group and is often called the restricted Lorentz group and is denoted SO+(1,3). The restricted Lorentz group consists of those Lorentz transformations that preserve the orientation
of space and direction of time. The restricted Lorentz group has often been presented through a facility of biquaternion algebra.
In pure mathematics, the restricted Lorentz group arises in another guise as the Möbius group, which is the symmetry group
of conformal geometry
on the Riemann sphere
. This observation was taken by Roger Penrose
as the starting point of twistor theory
. It has a fascinating physical consequence for the appearance of the night sky as seen by an observer who is maneuvering at relativistic velocities relative to the "fixed stars", which is discussed below.
The restricted Lorentz group arises in other ways in pure mathematics. For example, it arises as the point symmetry group of a certain ordinary differential equation
. This fact also has physical significance.
Note: the Lorentz group also preserves the quadratic form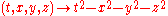
and is therefore sometimes denoted O(1,3). A similar remark applies to its identity component and the subgroups introduced below.
, the Lorentz group O(1,3) is both a group
and a smooth manifold. As a manifold, it has four connected component
s. Intuitively, this means that it consists of four topologically separated pieces.
To see why, notice that a Lorentz transformation may or may not
Lorentz transformations which preserve the direction of time are called orthochronous. Those which preserve orientation are called proper, and as linear transformations they have determinant +1. (The improper Lorentz transformations have determinant −1.) The subgroup of proper Lorentz transformations is denoted SO(1,3). The subgroup of orthochronous transformations is often denoted O+(1,3).
The identity component
of the Lorentz group is the set of all Lorentz transformations preserving both orientation and the direction of time. It is called the proper, orthochronous Lorentz group, or restricted Lorentz group, and it is denoted by SO+(1, 3). It is a normal subgroup
of the Lorentz group which is also six dimensional.
Note: Some authors refer to SO(1,3) or even O(1,3) when they actually mean SO+(1, 3).
The quotient group
O(1,3)/SO+(1,3) is isomorphic to the Klein four-group
. Every element in O(1,3) can be written as the semidirect product of a proper, orthochronous transformation and an element of the discrete group
where P and T are the space inversion and time reversal
operators:
The four elements of this isomorphic copy of the Klein four-group label the four connected components of the Lorentz group.
of the Lorentz group. This means that it consists of all Lorentz transformations which can be connected to the identity by a continuous curve lying in the group. The restricted Lorentz group is a connected normal subgroup
of the full Lorentz group with the same dimension (in this case, 6 dimensions).
The restricted Lorentz group is generated by ordinary spatial rotations and Lorentz boosts (which can be thought of as hyperbolic rotations in a plane that includes a time-like direction). The set of all rotations forms a Lie subgroup
isomorphic to the ordinary rotation group
SO(3). The set of all boosts, however, does not form a subgroup, since composing two boosts does not, in general, result in another boost. (Rather, a pair of non-colinear boosts is equivalent to a boost and a rotation, and this relates to Thomas rotation.)
A boost in some direction, or a rotation about some axis, each generate a one-parameter subgroup. An arbitrary rotation is specified by 3 real parameters
, as is an arbitrary boost. Since every proper, orthochronous Lorentz transformation can be written as a product of a rotation and a boost, it takes 6 real numbers (parameters) to specify an arbitrary proper orthochronous Lorentz transformation. This is one way to understand why the restricted Lorentz group is six dimensional. (We'll study this in more detail in a later section on the Lie algebra of the Lorentz group.) To specify an arbitrary Lorentz transformation requires a further two bits of information, which pick out one of the four connected components. This pattern is typical of finite dimensional Lie groups.
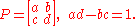
We can write two by two Hermitian matrices in the form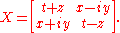
This trick has the pleasant feature that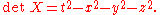
Therefore, we have identified the space of Hermitian matrices (which is four dimensional, as real vector space)
with Minkowski spacetime in such a way that the determinant of a Hermitian matrix is the squared length of the corresponding vector in Minkowski spacetime.
But now SL(2,C) acts on the space of Hermitian matrices via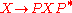
where
is the Hermitian transpose
of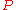
, and this action preserves the determinant. Therefore, SL(2,C) acts on Minkowski spacetime by (linear) isometries. We have now constructed a homomorphism
of Lie groups from SL(2,C) onto SO+(1,3), which we will call the spinor map. The kernel of the spinor map is the two element subgroup ±I. Therefore, the quotient group PSL(2,C) is isomorphic to SO+(1,3).
with a null vector
in Minkowski space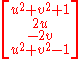
or the Hermitian matrix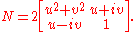
The set of real scalar multiples of this null vector, which we can call a null line through the origin, represents a line of sight from an observer at a particular place and time (an arbitrary event which we can identify with the origin of Minkowski spacetime) to various distant objects, such as stars.
But by stereographic projection
, we can identify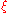
with a point on the Riemann sphere
. Putting it all together, we have identified the points of the celestial sphere
with certain Hermitian matrices, and also with lines of sight. This implies that the Möbius transformations of the Riemann sphere precisely represent
the way that Lorentz transformations change the appearance of the celestial sphere.
For our purposes here, we can pretend that the "fixed stars" live in Minkowski spacetime. Then, the Earth is moving at a nonrelativistic velocity with respect to a typical astronomical object which might be visible at night. But, an observer who is moving at relativistic
velocity with respect to the Earth would see the appearance of the night sky (as modeled by points on the celestial sphere) transformed by a Möbius transformation.
(To be utterly pedantic, the identity element is in a fifth class, all by itself.)
In the article on Möbius transformations, it is explained how this classification arises by considering the fixed point
s of Möbius transformations in their action on the Riemann sphere, which corresponds here to null
eigenspaces of restricted Lorentz transformations in their action on Minkowski spacetime.
We will discuss a particularly simple example of each type, and in particular, the effect (e.g., on the appearance of the night sky)
of the one-parameter subgroup which it generates. At the end of the section we will briefly indicate how we can understand the effect of general Lorentz transformations on the appearance of the night sky in terms of these examples.
A typical elliptic element of SL(2,C) is
which has fixed points
. Writing out the action 
and collecting terms, we find that our spinor map takes this to the (restricted) Lorentz transformation
This transformation represents a rotation about the z axis. The one-parameter subgroup it generates is obtained by simply taking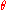
to be a real variable instead of a constant. The corresponding continuous transformations of the celestial sphere (except for the identity) all share the same two fixed points, the North and South pole. They move all other points around latitude circles. In other words, this group yields a continuous counterclockwise rotation about the z axis as 
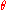increases.
Notice the angle doubling; this phenomenon is a characteristic feature of spinorial double coverings.
A typical hyperbolic element of SL(2,C) is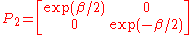
which also has fixed points
. Under stereographic projection from the Riemann sphere to the Euclidean plane, the effect of this Möbius transformation is a dilation from the origin. Our homomorphism maps this to the Lorentz transformation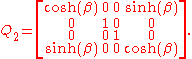
This transformation represents a boost along the z axis. The one-parameter subgroup it generates is obtained by simply taking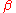
to be a real variable instead of a constant. The corresponding continuous transformations of the celestial sphere (except for the identity) all share the same fixed points (the North and South poles), and they move all other points along longitude
s away from the South pole and toward the North pole.
A typical loxodromic element of SL(2,C) is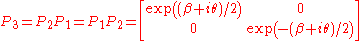
which also has fixed points
. Our homomorphism maps this to the Lorentz transformation
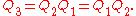
The one-parameter subgroup this generates is obtained by replacing
with any real multiple of this complex constant. (If we let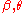 
vary independently, we obtain a two-dimensional abelian subgroup
, consisting of simultaneous rotations about the z axis and boosts along the z axis; in contrast, the one-dimensional subgroup we are discussing here consists of those elements of this two-dimensional subgroup such that the rapidity of the boost and angle of the rotation have a fixed ratio.) The corresponding continuous transformations of the celestial sphere (always excepting the identity) all share the same two fixed points (the North and South poles). They move all other points away from the South pole and toward the North pole (or vice versa), along a family of curves called loxodromes. Each loxodrome spirals infinitely often around each pole.
A typical parabolic element of SL(2,C) is
which has the single fixed point
on the Riemann sphere. Under stereographic projection, it appears as ordinary translation
along the real axis. Our homomorphism maps this to the matrix (representing a Lorentz transformation)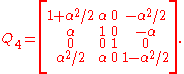
This generates a one-parameter subgroup which is obtained by considering
to be a real variable rather than a constant. The corresponding continuous transformations of the celestial sphere move points along a family of circles which are all tangent at the North pole to a certain great circle
. All points other than the North pole itself move along these circles. (Except, of course, for the identity transformation.)
Parabolic Lorentz transformations are often called null rotations. Since these are likely to be the least familiar of the four types of nonidentity Lorentz transformations (elliptic, hyperbolic, loxodromic, parabolic), we will show how to determine the effect of our example of a parabolic Lorentz transformation on Minkowski spacetime, leaving the other examples as exercises for the reader. From the matrix given above we can read off the transformation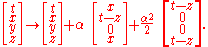
Differentiating this transformation with respect to the group parameter
and evaluate at
, we read off the corresponding vector field (first order linear partial differential operator)
Apply this to an undetermined function
. The solution of the resulting first order linear partial differential equation can be expressed in the form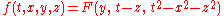
where
is an arbitrary smooth function. The arguments on the right hand side now give three rational invariants describing how points (events) move under our parabolic transformation:
(The reader can verify that these quantities standing on the left hand sides are invariant under our transformation.) Choosing real values for the constants standing on the right hand sides gives three conditions, and thus defines a curve in Minkowski spacetime. This curve is one of the flowlines of our transformation. We see from the form of the rational invariants that these flowlines (or orbits) have a very simple description: suppressing the inessential coordinate y, we see that each orbit is the intersection of a null plane
with a hyperboloid 
. In particular, the reader may wish to sketch the case 
, in which the hyperboloid degenerates to a light cone; then orbits are parabolas lying in null planes just mentioned.
Parabolic transformations lead to the gauge symmetry of massless particles with helicity
.
Notice that a particular null line lying in the light cone is left invariant; this corresponds to the unique (double) fixed point on the Riemann sphere which was mentioned above. The other null lines through the origin are "swung around the cone" by the transformation. Following the motion of one such null line as
increases corresponds to following the motion of a point along one of the circular flow lines on the celestial sphere, as described above.
The Möbius transformations are precisely the conformal transformations
of the Riemann sphere (or celestial sphere). It follows that by conjugating with an arbitrary element of SL(2,C), we can obtain from the above examples arbitrary elliptic, hyperbolic, loxodromic, and parabolic (restricted) Lorentz transformations, respectively. The effect on the flow lines of the corresponding one-parameter subgroups is to transform the pattern seen in our examples by some conformal transformation. Thus, an arbitrary elliptic Lorentz transformation can have any two distinct fixed points on the celestial sphere, but points will still flow along circular arcs from one fixed point toward the other. Similarly for the other cases.
Finally, arbitrary Lorentz transformations can be obtained from the restricted ones by multiplying by a matrix which reflects across
, or by an appropriate orientation reversing diagonal matrix.
. Since the Lorentz group is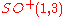
, its Lie algebra
is reducible and can be decomposed to two copies of the Lie algebra
of SL(2,R), as will be shown explicitly below (this is the Minkowski space
analog of the SO(4)
SU(2)
SU(2) decomposition in a Euclidean space
).
In particle physics
, a state that is invariant under one of these copies of SL(2,R) is said to have chirality
, and is either left-handed or right-handed, according to which copy of SL(2,R) it is invariant under.
The Lorentz group is a subgroup of the diffeomorphism group of R4 and therefore its Lie algebra can be identified with vector fields on R4. In particular, the vectors which generate isometries on a space are its Killing vectors, which provides a convenient alternative to the left-invariant vector field for calculating the Lie algebra. We can immediately write down an obvious set of six generators:
It may be helpful to briefly recall here how to obtain a one-parameter group from a vector field
, written in the form of a first order linear
partial differential operator such as
The corresponding initial value problem is
The solution can be written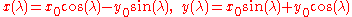
or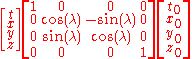
where we easily recognize the one-parameter matrix group of rotations about the z axis.
Differentiating with respect to the group parameter and setting
in the result, we recover the matrix
which corresponds to the vector field we started with. This shows how to pass between matrix and vector field representations of elements of the Lie algebra.
Reversing the procedure in the previous section, we see that the Möbius transformations which correspond to our six generators arise from exponentiating respectively
(for the three boosts) or 
(for the three rotations) times the three Pauli matrices
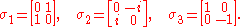
For our purposes, another generating set is more convenient. We list the six generators in the following table, in which
Notice that the generators consist of
Let's verify one line in this table. Start with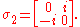
Exponentiate: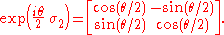
This element of SL(2,C) represents the one-parameter subgroup of (elliptic) Möbius transformations: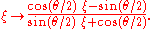
Next,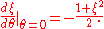
The corresponding vector field on C (thought of as the image of S2 under stereographic projection) is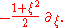
Writing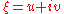
, this becomes the vector field on R2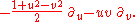
Returning to our element of SL(2,C), writing out the action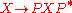
and collecting terms, we find that the image under the spinor map is the element of SO+(1,3)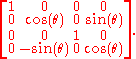
Differentiating with respect the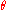
at 
, we find that the corresponding vector field on R4 is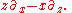
This is evidently the generator of counterclockwise rotation about the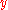
axis.
The one-dimensional subalgebras of course correspond to the four conjugacy classes of elements of the Lorentz group:
(Strictly speaking the last corresponds to infinitely many classes, since distinct
give different classes.)
The two-dimensional subalgebras are:
The three dimensional subalgebras are:
(Here, the Bianchi types
refer to the classification of three dimensional Lie algebras by the Italian mathematician Luigi Bianchi
.)
The four dimensional subalgebras are all conjugate to
The subalgebras form a lattice (see the figure), and each subalgebra generates by exponentiation a closed subgroup of the restricted Lie group. From these, all subgroups of the Lorentz group can be constructed, up to conjugation, by multiplying by one of the elements of the Klein four-group.
As with any connected Lie group, the coset spaces of the closed subgroups of the restricted Lorentz group, or homogeneous spaces, have considerable mathematical interest. We briefly describe some of them here:
SO+(1,3), which we called the spinor map. Since SL(2,C) is simply connected, it is the covering group of the restricted Lorentz group SO+(1,3). By restriction we obtain a homomorphism SU(2) 
SO(3). Here, the special unitary group
SU(2), which is isomorphic to the group of unit norm
quaternion
s, is also simply connected, so it is the covering group of the rotation group SO(3).
Each of these covering map
s are twofold covers in the sense that precisely two elements of the covering group map to each element of the quotient. One often says that the restricted Lorentz group and the rotation group are doubly connected. This means that the fundamental group
of the each group is isomorphic to the two element cyclic group
Z2.
Warning: in applications to quantum mechanics
the special linear group
SL(2, C) is sometimes called the Lorentz group.
Twofold coverings are characteristic of spin groups. Indeed, in addition to the double coverings
we have the double coverings
These spinorial double coverings are all closely related to Clifford algebras.
are deformation retract
s of the left and right groups, respectively, in the double covering
But the homogeneous space SO+(1,3)/SO(3) is homeomorphic to hyperbolic 3-space H3, so we have exhibited the restricted Lorentz group as a principal fiber bundle
with fibers SO(3) and base H3. Since the latter is homeomorphic to R3, while SO(3) is homeomorphic to three-dimensional real projective space
RP3, we see that the restricted Lorentz group is locally homeomorphic to the product of RP3 with R3. Since the base space is contractible, this can be extended to a global homeomorphism.
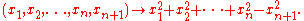
Many of the properties of the Lorentz group in four dimensions (n=3) generalize straightforwardly to arbitrary n. For instance, the Lorentz group O(n,1) has four connected components, and it acts by conformal transformations on the celestial (n-1)-sphere in n+1 dimensional Minkowski space. The identity component SO+(n,1) is an SO(n)-bundle over hyperbolic n-space Hn.
The low dimensional cases n=1 and n=2 are often useful as "toy models" for the physical case n=3, while higher dimensional Lorentz groups are used in physical theories such as string theory
which posit the existence of hidden dimensions. The Lorentz group O(n,1) is also the isometry group of n-dimensional de Sitter space
dSn, which may be realized as the homogeneous space O(n,1)/O(n-1,1). In particular O(4,1) is the isometry group of the de Sitter universe
dS4, a cosmological model.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
(and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
), the Lorentz group is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s of Minkowski spacetime, the classical
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
setting for all (nongravitational) physical phenomena
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. The Lorentz group is named for the Dutch
Dutch people
The Dutch people are an ethnic group native to the Netherlands. They share a common culture and speak the Dutch language. Dutch people and their descendants are found in migrant communities worldwide, notably in Suriname, Chile, Brazil, Canada, Australia, South Africa, New Zealand, and the United...
physicist Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
.
The mathematical form of
- the kinematical lawsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
of special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, - Maxwell's field equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
in the theory of electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, - Dirac's equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
in the theory of the electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
,
are each invariant under the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s. Therefore the Lorentz group is said to express the fundamental symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of many of the known fundamental Laws of Nature.
Basic properties
The Lorentz group is a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
, the group of all isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Minkowski space-time. The Lorentz transformations are precisely the isometries which leave the origin fixed. Thus, the Lorentz group is an isotropy subgroup of the isometry group of Minkowski spacetime. For this reason, the Lorentz group is sometimes called the homogeneous Lorentz group while the Poincaré group is sometimes called the inhomogeneous Lorentz group. Lorentz transformations are examples of linear transformations; general isometries of Minkowski spacetime are affine transformations.
Mathematically, the Lorentz group may be described as the generalized orthogonal group
Generalized orthogonal group
In mathematics, the indefinite orthogonal group, O is the Lie group of all linear transformations of a n = p + q dimensional real vector space which leave invariant a nondegenerate, symmetric bilinear form of signature...
O(1,3), the matrix Lie group which preserves the quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on R4. This quadratic form is interpreted in physics as the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
of Minkowski spacetime, so this definition is simply a restatement of the fact that Lorentz transformations are precisely the linear transformations which are also isometries of Minkowski spacetime.
The Lorentz group is a six-dimensional
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
noncompact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
real Lie group which is not connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. All four of its connected components are not simply connected. The identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
(i.e. the component containing the identity element) of the Lorentz group is itself a group and is often called the restricted Lorentz group and is denoted SO+(1,3). The restricted Lorentz group consists of those Lorentz transformations that preserve the orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of space and direction of time. The restricted Lorentz group has often been presented through a facility of biquaternion algebra.
In pure mathematics, the restricted Lorentz group arises in another guise as the Möbius group, which is the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of conformal geometry
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. This observation was taken by Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
as the starting point of twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
. It has a fascinating physical consequence for the appearance of the night sky as seen by an observer who is maneuvering at relativistic velocities relative to the "fixed stars", which is discussed below.
The restricted Lorentz group arises in other ways in pure mathematics. For example, it arises as the point symmetry group of a certain ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
. This fact also has physical significance.
Note: the Lorentz group also preserves the quadratic form
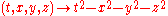and is therefore sometimes denoted O(1,3). A similar remark applies to its identity component and the subgroups introduced below.Connected components
Because it is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, the Lorentz group O(1,3) is both a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and a smooth manifold. As a manifold, it has four connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
s. Intuitively, this means that it consists of four topologically separated pieces.
To see why, notice that a Lorentz transformation may or may not
- reverse the direction of time (or more precisely, transform a future-pointing timelike vector into a past-pointing one),
- reverse the orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of a vierbein(tetrad).
Lorentz transformations which preserve the direction of time are called orthochronous. Those which preserve orientation are called proper, and as linear transformations they have determinant +1. (The improper Lorentz transformations have determinant −1.) The subgroup of proper Lorentz transformations is denoted SO(1,3). The subgroup of orthochronous transformations is often denoted O+(1,3).
The identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the Lorentz group is the set of all Lorentz transformations preserving both orientation and the direction of time. It is called the proper, orthochronous Lorentz group, or restricted Lorentz group, and it is denoted by SO+(1, 3). It is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of the Lorentz group which is also six dimensional.
Note: Some authors refer to SO(1,3) or even O(1,3) when they actually mean SO+(1, 3).
The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
O(1,3)/SO+(1,3) is isomorphic to the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
. Every element in O(1,3) can be written as the semidirect product of a proper, orthochronous transformation and an element of the discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
- {1, P, T, PT}
where P and T are the space inversion and time reversal
T-symmetry
T Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...
operators:
- P = diag(1, −1, −1, −1)
- T = diag(−1, 1, 1, 1).
The four elements of this isomorphic copy of the Klein four-group label the four connected components of the Lorentz group.
The restricted Lorentz group
As stated above, the restricted Lorentz group is the identity componentIdentity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the Lorentz group. This means that it consists of all Lorentz transformations which can be connected to the identity by a continuous curve lying in the group. The restricted Lorentz group is a connected normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of the full Lorentz group with the same dimension (in this case, 6 dimensions).
The restricted Lorentz group is generated by ordinary spatial rotations and Lorentz boosts (which can be thought of as hyperbolic rotations in a plane that includes a time-like direction). The set of all rotations forms a Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
isomorphic to the ordinary rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3). The set of all boosts, however, does not form a subgroup, since composing two boosts does not, in general, result in another boost. (Rather, a pair of non-colinear boosts is equivalent to a boost and a rotation, and this relates to Thomas rotation.)
A boost in some direction, or a rotation about some axis, each generate a one-parameter subgroup. An arbitrary rotation is specified by 3 real parameters
Charts on SO(3)
In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
, as is an arbitrary boost. Since every proper, orthochronous Lorentz transformation can be written as a product of a rotation and a boost, it takes 6 real numbers (parameters) to specify an arbitrary proper orthochronous Lorentz transformation. This is one way to understand why the restricted Lorentz group is six dimensional. (We'll study this in more detail in a later section on the Lie algebra of the Lorentz group.) To specify an arbitrary Lorentz transformation requires a further two bits of information, which pick out one of the four connected components. This pattern is typical of finite dimensional Lie groups.
Relation to the Möbius group
The restricted Lorentz group SO+(1, 3) is isomorphic to the Möbius group, which is, in turn, isomorphic to the projective special linear group PSL(2,C). It will be convenient to work at first with SL(2,C). This group consists of all two by two complex matrices with determinant one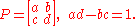We can write two by two Hermitian matrices in the form
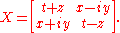
This trick has the pleasant feature that
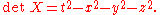
Therefore, we have identified the space of Hermitian matrices (which is four dimensional, as real vector space)
with Minkowski spacetime in such a way that the determinant of a Hermitian matrix is the squared length of the corresponding vector in Minkowski spacetime.
But now SL(2,C) acts on the space of Hermitian matrices via
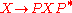
where
is the Hermitian transposeHermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of
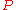, and this action preserves the determinant. Therefore, SL(2,C) acts on Minkowski spacetime by (linear) isometries. We have now constructed a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of Lie groups from SL(2,C) onto SO+(1,3), which we will call the spinor map. The kernel of the spinor map is the two element subgroup ±I. Therefore, the quotient group PSL(2,C) is isomorphic to SO+(1,3).
Appearance of the night sky
This isomorphism has a very interesting physical interpretation. We can identify the complex numberwith a null vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
in Minkowski space
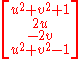
or the Hermitian matrix
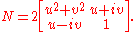
The set of real scalar multiples of this null vector, which we can call a null line through the origin, represents a line of sight from an observer at a particular place and time (an arbitrary event which we can identify with the origin of Minkowski spacetime) to various distant objects, such as stars.
But by stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
, we can identify
with a point on the Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Putting it all together, we have identified the points of the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
with certain Hermitian matrices, and also with lines of sight. This implies that the Möbius transformations of the Riemann sphere precisely represent
the way that Lorentz transformations change the appearance of the celestial sphere.
For our purposes here, we can pretend that the "fixed stars" live in Minkowski spacetime. Then, the Earth is moving at a nonrelativistic velocity with respect to a typical astronomical object which might be visible at night. But, an observer who is moving at relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
velocity with respect to the Earth would see the appearance of the night sky (as modeled by points on the celestial sphere) transformed by a Möbius transformation.
Conjugacy classes
Because the restricted Lorentz group SO+(1, 3) is isomorphic to the Möbius group PSL(2,C), its conjugacy classes also fall into four classes:- elliptic transformations
- hyperbolic transformations
- loxodromic transformations
- parabolic transformations
(To be utterly pedantic, the identity element is in a fifth class, all by itself.)
In the article on Möbius transformations, it is explained how this classification arises by considering the fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of Möbius transformations in their action on the Riemann sphere, which corresponds here to null
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
eigenspaces of restricted Lorentz transformations in their action on Minkowski spacetime.
We will discuss a particularly simple example of each type, and in particular, the effect (e.g., on the appearance of the night sky)
of the one-parameter subgroup which it generates. At the end of the section we will briefly indicate how we can understand the effect of general Lorentz transformations on the appearance of the night sky in terms of these examples.
A typical elliptic element of SL(2,C) is
which has fixed points
. Writing out the action and collecting terms, we find that our spinor map takes this to the (restricted) Lorentz transformationThis transformation represents a rotation about the z axis. The one-parameter subgroup it generates is obtained by simply taking
to be a real variable instead of a constant. The corresponding continuous transformations of the celestial sphere (except for the identity) all share the same two fixed points, the North and South pole. They move all other points around latitude circles. In other words, this group yields a continuous counterclockwise rotation about the z axis as increases.Notice the angle doubling; this phenomenon is a characteristic feature of spinorial double coverings.
A typical hyperbolic element of SL(2,C) is
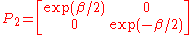
which also has fixed points
. Under stereographic projection from the Riemann sphere to the Euclidean plane, the effect of this Möbius transformation is a dilation from the origin. Our homomorphism maps this to the Lorentz transformation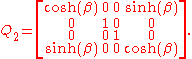This transformation represents a boost along the z axis. The one-parameter subgroup it generates is obtained by simply taking
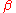to be a real variable instead of a constant. The corresponding continuous transformations of the celestial sphere (except for the identity) all share the same fixed points (the North and South poles), and they move all other points along longitudeLongitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
s away from the South pole and toward the North pole.
A typical loxodromic element of SL(2,C) is
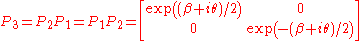
which also has fixed points
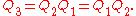
. Our homomorphism maps this to the Lorentz transformationThe one-parameter subgroup this generates is obtained by replacing
with any real multiple of this complex constant. (If we let 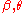vary independently, we obtain a two-dimensional abelian subgroupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, consisting of simultaneous rotations about the z axis and boosts along the z axis; in contrast, the one-dimensional subgroup we are discussing here consists of those elements of this two-dimensional subgroup such that the rapidity of the boost and angle of the rotation have a fixed ratio.) The corresponding continuous transformations of the celestial sphere (always excepting the identity) all share the same two fixed points (the North and South poles). They move all other points away from the South pole and toward the North pole (or vice versa), along a family of curves called loxodromes. Each loxodrome spirals infinitely often around each pole.
A typical parabolic element of SL(2,C) is
which has the single fixed point
on the Riemann sphere. Under stereographic projection, it appears as ordinary translationTranslation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
along the real axis. Our homomorphism maps this to the matrix (representing a Lorentz transformation)
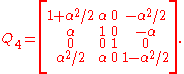
This generates a one-parameter subgroup which is obtained by considering
to be a real variable rather than a constant. The corresponding continuous transformations of the celestial sphere move points along a family of circles which are all tangent at the North pole to a certain great circleGreat circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
. All points other than the North pole itself move along these circles. (Except, of course, for the identity transformation.)
Parabolic Lorentz transformations are often called null rotations. Since these are likely to be the least familiar of the four types of nonidentity Lorentz transformations (elliptic, hyperbolic, loxodromic, parabolic), we will show how to determine the effect of our example of a parabolic Lorentz transformation on Minkowski spacetime, leaving the other examples as exercises for the reader. From the matrix given above we can read off the transformation
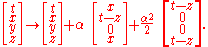
Differentiating this transformation with respect to the group parameter
and evaluate at, we read off the corresponding vector field (first order linear partial differential operator)Apply this to an undetermined function
. The solution of the resulting first order linear partial differential equation can be expressed in the form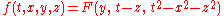where
is an arbitrary smooth function. The arguments on the right hand side now give three rational invariants describing how points (events) move under our parabolic transformation:(The reader can verify that these quantities standing on the left hand sides are invariant under our transformation.) Choosing real values for the constants standing on the right hand sides gives three conditions, and thus defines a curve in Minkowski spacetime. This curve is one of the flowlines of our transformation. We see from the form of the rational invariants that these flowlines (or orbits) have a very simple description: suppressing the inessential coordinate y, we see that each orbit is the intersection of a null plane
with a hyperboloid . In particular, the reader may wish to sketch the case , in which the hyperboloid degenerates to a light cone; then orbits are parabolas lying in null planes just mentioned.Parabolic transformations lead to the gauge symmetry of massless particles with helicity
.Notice that a particular null line lying in the light cone is left invariant; this corresponds to the unique (double) fixed point on the Riemann sphere which was mentioned above. The other null lines through the origin are "swung around the cone" by the transformation. Following the motion of one such null line as
increases corresponds to following the motion of a point along one of the circular flow lines on the celestial sphere, as described above.The Möbius transformations are precisely the conformal transformations
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
of the Riemann sphere (or celestial sphere). It follows that by conjugating with an arbitrary element of SL(2,C), we can obtain from the above examples arbitrary elliptic, hyperbolic, loxodromic, and parabolic (restricted) Lorentz transformations, respectively. The effect on the flow lines of the corresponding one-parameter subgroups is to transform the pattern seen in our examples by some conformal transformation. Thus, an arbitrary elliptic Lorentz transformation can have any two distinct fixed points on the celestial sphere, but points will still flow along circular arcs from one fixed point toward the other. Similarly for the other cases.
Finally, arbitrary Lorentz transformations can be obtained from the restricted ones by multiplying by a matrix which reflects across
, or by an appropriate orientation reversing diagonal matrix.The Lie algebra of the Lorentz group
As with any Lie group, the best way to study many aspects of the Lorentz group is via its Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. Since the Lorentz group is
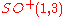, its Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is reducible and can be decomposed to two copies of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SL(2,R), as will be shown explicitly below (this is the Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
analog of the SO(4)
SU(2)SU(2) decomposition in a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
).
In particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, a state that is invariant under one of these copies of SL(2,R) is said to have chirality
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
, and is either left-handed or right-handed, according to which copy of SL(2,R) it is invariant under.
The Lorentz group is a subgroup of the diffeomorphism group of R4 and therefore its Lie algebra can be identified with vector fields on R4. In particular, the vectors which generate isometries on a space are its Killing vectors, which provides a convenient alternative to the left-invariant vector field for calculating the Lie algebra. We can immediately write down an obvious set of six generators:
- vector fields on R4 generating three rotations
- vector fields on R4 generating three boosts
It may be helpful to briefly recall here how to obtain a one-parameter group from a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, written in the form of a first order linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
partial differential operator such as
The corresponding initial value problem is
The solution can be written
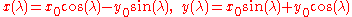
or
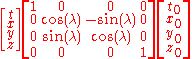
where we easily recognize the one-parameter matrix group of rotations about the z axis.
Differentiating with respect to the group parameter and setting
in the result, we recover the matrixwhich corresponds to the vector field we started with. This shows how to pass between matrix and vector field representations of elements of the Lie algebra.
Reversing the procedure in the previous section, we see that the Möbius transformations which correspond to our six generators arise from exponentiating respectively
(for the three boosts) or (for the three rotations) times the three Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
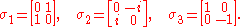
For our purposes, another generating set is more convenient. We list the six generators in the following table, in which
- the first column gives a generator of the flow under the Möbius action (after stereographic projection from the Riemann sphere) as a real vector field on the Euclidean plane,
- the second column gives the corresponding one-parameter subgroup of Möbius transformations,
- the third column gives the corresponding one-parameter subgroup of Lorentz transformations (the image under our homomorphism of preceding one-parameter subgroup),
- the fourth column gives the corresponding generator of the flow under the Lorentz action as a real vector field on Minkowski spacetime.
Notice that the generators consist of
- two parabolics (null rotations),
- one hyperbolic (boost in
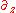direction), - three elliptics (rotations about x,y,z axes respectively).
| Vector field on R2 | One-parameter subgroup of SL(2,C), representing Möbius transformations |
One-parameter subgroup of SO+(1,3), representing Lorentz transformations |
Vector field on R4 |
|---|---|---|---|
| Parabolic | |||
 |
 |
 |
  |
 |
 |
 |
  |
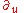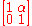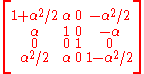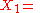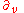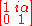| Hyperbolic | |||
 |
 |
 |
  |
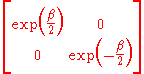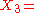| Elliptic | |||
 |
 |
 |
  |
 |
 |
 |
  |
 |
 |
 |
  |
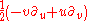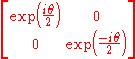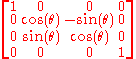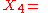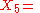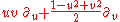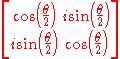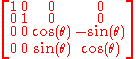Let's verify one line in this table. Start with
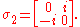
Exponentiate:
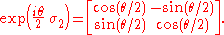
This element of SL(2,C) represents the one-parameter subgroup of (elliptic) Möbius transformations:
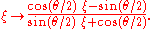
Next,
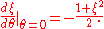
The corresponding vector field on C (thought of as the image of S2 under stereographic projection) is
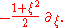
Writing
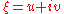, this becomes the vector field on R2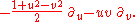Returning to our element of SL(2,C), writing out the action
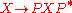and collecting terms, we find that the image under the spinor map is the element of SO+(1,3)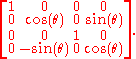Differentiating with respect the
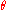at , we find that the corresponding vector field on R4 is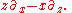This is evidently the generator of counterclockwise rotation about the
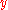axis.Subgroups of the Lorentz group
The subalgebras of the Lie algebra of the Lorentz group can be enumerated, up to conjugacy, from which we can list the closed subgroups of the restricted Lorentz group, up to conjugacy. (See the book by Hall cited below for the details.) We can readily express the result in terms of the generating set given in the table above.The one-dimensional subalgebras of course correspond to the four conjugacy classes of elements of the Lorentz group:
generates a one-parameter subalgebra of parabolics SO(0,1),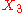
generates a one-parameter subalgebra of boosts SO(1,1),
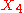generates a one-parameter of rotations SO(2),
(for any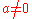 
) generates a one-parameter subalgebra of loxodromic transformations.
(Strictly speaking the last corresponds to infinitely many classes, since distinct
give different classes.)The two-dimensional subalgebras are:
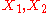generate an abelian subalgebra consisting entirely of parabolics,
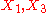generate a nonabelian subalgebra isomorphic to the Lie algebra of the affine group A(1),
generate an abelian subalgebra consisting of boosts, rotations, and loxodromics all sharing the same pair of fixed points.
The three dimensional subalgebras are:
generate a Bianchi V subalgebra, isomorphic to the Lie algebra of Hom(2), the group of euclidean homotheties,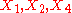
generate a Bianchi VII_0 subalgebra, isomorphic to the Lie algebra of E(2), the euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
,
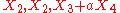, where 
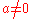, generate a Bianchi VII_a subalgebra,
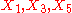generate a Bianchi VIII subalgebra, isomorphic to the Lie algebra of SL(2,R), the group of isometries of the hyperbolic planePoincaré half-plane modelIn non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
,
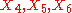generate a Bianchi IX subalgebra, isomorphic to the Lie algebra of SO(3), the rotation group.
(Here, the Bianchi types
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
refer to the classification of three dimensional Lie algebras by the Italian mathematician Luigi Bianchi
Luigi Bianchi
- External links :* offers translations of some of Bianchi's papers, plus a biography of Bianchi.* PDF copy at * * * *...
.)
The four dimensional subalgebras are all conjugate to
generate a subalgebra isomorphic to the Lie algebra of Sim(2), the group of Euclidean similitudesSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
.
The subalgebras form a lattice (see the figure), and each subalgebra generates by exponentiation a closed subgroup of the restricted Lie group. From these, all subgroups of the Lorentz group can be constructed, up to conjugation, by multiplying by one of the elements of the Klein four-group.
As with any connected Lie group, the coset spaces of the closed subgroups of the restricted Lorentz group, or homogeneous spaces, have considerable mathematical interest. We briefly describe some of them here:
- the group Sim(2) is the stabilizer of a null line, i.e. of a point on the Riemann sphere, so the homogeneous space SO+(1,3)/Sim(2) is the Kleinian geometry which represents conformal geometryConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
on the sphere S2, - the (identity component of the) Euclidean group SE(2) is the stabilizer of a null vectorNull vectorNull vector can refer to:* Null vector * A causal structure in Minkowski space...
, so the homogeneous space SO+(1,3)/SE(2) is the momentum space of a massless particle; geometrically, this Kleinian geometry represents the degenerate geometry of the light cone in Minkowski spacetime, - the rotation group SO(3) is the stabilizer of a timelike vector, so the homogeneous space SO+(1,3)/SO(3) is the momentum space of a massive particle; geometrically, this space is none other than three-dimensional hyperbolic spaceHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
H3.
Covering groups
In a previous section we constructed a homomorphism SL(2,C) SO+(1,3), which we called the spinor map. Since SL(2,C) is simply connected, it is the covering group of the restricted Lorentz group SO+(1,3). By restriction we obtain a homomorphism SU(2) SO(3). Here, the special unitary groupSpecial unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(2), which is isomorphic to the group of unit norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, is also simply connected, so it is the covering group of the rotation group SO(3).
Each of these covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
s are twofold covers in the sense that precisely two elements of the covering group map to each element of the quotient. One often says that the restricted Lorentz group and the rotation group are doubly connected. This means that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the each group is isomorphic to the two element cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z2.
Warning: in applications to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2, C) is sometimes called the Lorentz group.
Twofold coverings are characteristic of spin groups. Indeed, in addition to the double coverings
- Spin+(1,3)=SL(2,C)
SO+(1,3) - Spin(3)=SU(2)
SO(3)
we have the double coverings
- Pin(1,3)Pin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
O(1,3) - Spin(1,3)
SO(1,3) - Spin+(1,2) = SU(1,1)
SO(1,2)
These spinorial double coverings are all closely related to Clifford algebras.
Topology
The left and right groups in the double covering- SU(2)
SO(3)
are deformation retract
Deformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
s of the left and right groups, respectively, in the double covering
- SL(2,C)
SO+(1,3).
But the homogeneous space SO+(1,3)/SO(3) is homeomorphic to hyperbolic 3-space H3, so we have exhibited the restricted Lorentz group as a principal fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
with fibers SO(3) and base H3. Since the latter is homeomorphic to R3, while SO(3) is homeomorphic to three-dimensional real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
RP3, we see that the restricted Lorentz group is locally homeomorphic to the product of RP3 with R3. Since the base space is contractible, this can be extended to a global homeomorphism.
General dimensions
The concept of the Lorentz group has a natural generalization to any spacetime dimension. Mathematically, the Lorentz group of n+1 dimensional Minkowski space is the group O(n,1) (or O(1,n)) of linear transformations of Rn+1 which preserve the quadratic form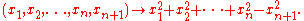Many of the properties of the Lorentz group in four dimensions (n=3) generalize straightforwardly to arbitrary n. For instance, the Lorentz group O(n,1) has four connected components, and it acts by conformal transformations on the celestial (n-1)-sphere in n+1 dimensional Minkowski space. The identity component SO+(n,1) is an SO(n)-bundle over hyperbolic n-space Hn.
The low dimensional cases n=1 and n=2 are often useful as "toy models" for the physical case n=3, while higher dimensional Lorentz groups are used in physical theories such as string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
which posit the existence of hidden dimensions. The Lorentz group O(n,1) is also the isometry group of n-dimensional de Sitter space
De Sitter space
In mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
dSn, which may be realized as the homogeneous space O(n,1)/O(n-1,1). In particular O(4,1) is the isometry group of the de Sitter universe
De Sitter universe
A de Sitter universe is a cosmological solution to Einstein's field equations of General Relativity which is named after Willem de Sitter. It models the universe as spatially flat and neglects ordinary matter, so the dynamics of the universe are dominated by the cosmological constant, thought to...
dS4, a cosmological model.