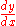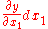Differential of a function
Encyclopedia
In calculus
, the differential represents the principal part of the change in a function y = ƒ(x) with respect to changes in the independent variable. The differential dy is defined by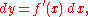
where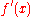
is the derivative
of ƒ with respect to x, and dx is an additional real variable
(so that dy is a function of x and dx). The notation is such that the equation
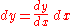
holds, where the derivative is represented in the Leibniz notation
dy/dx, and this is consistent with regarding the derivative as the quotient of the differentials. One also writes
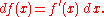
The precise meaning of the variables dy and dx depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form
, or analytical significance if the differential is regarded as a linear approximation
to the increment of a function. In physical applications, the variables dx and dy are often constrained to be very small ("infinitesimal
").
) change in the value y of the function, corresponding to an infinitely small change dx in the function's argument x. For that reason, the instantaneous rate of change of y with respect to x, which is the value of the derivative
of the function, is denoted by the fraction
in what is called the Leibniz notation
for derivatives. The quotient dy/dx is not infinitely small; rather it is a real number
.
The use of infinitesimals in this form was widely criticized, for instance by the famous pamphlet The Analyst
by Bishop Berkeley. Augustin-Louis Cauchy (1823) defined the differential without appeal to the atomism of Leibniz's infinitesimals. Instead, Cauchy, following d'Alembert
, inverted the logical order of Leibniz and his successors: the derivative itself became the fundamental object, defined as a limit
of difference quotients, and the differentials were then defined in terms of it. That is, one was free to define the differential dy by an expression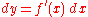
in which dy and dx are simply new variables taking finite real values, not fixed infinitesimals as they had been for Leibniz.
According to , Cauchy's approach was a significant logical improvement over the infinitesimal approach of Leibniz because, instead of invoking the metaphysical notion of infinitesimals, the quantities dy and dx could now be manipulated in exactly the same manner as any other real quantities
in a meaningful way. Cauchy's overall conceptual approach to differentials remains the standard one in modern analytical treatments, although the final word on rigor, a fully modern notion of the limit, was ultimately due to Karl Weierstrass
.
In physical treatments, such as those applied to the theory of thermodynamics
, the infinitesimal view still prevails. reconcile the physical use of infinitesimal differentials with the mathematical impossibility of them as follows. The differentials represent finite non-zero values that are smaller than the degree of accuracy required for the particular purpose for which they are intended. Thus "physical infinitesimals" need not appeal to a corresponding mathematical infinitesimal in order to have a precise sense.
Following twentieth-century developments in mathematical analysis
and differential geometry, it became clear that the notion of the differential of a function could be extended in a variety of ways. In real analysis
, it is more desirable to deal directly with the differential as the principal part of the increment of a function. This leads directly to the notion that the differential of a function at a point is linear functional
of an increment Δx. This approach allows the differential (as a linear map) to be developed for a variety of more sophisticated spaces, ultimately giving rise to such notions as the Fréchet
or Gâteaux derivative
. Likewise, in differential geometry, the differential of a function at a point is a linear function of a tangent vector
(an "infinitely small displacement"), which exhibits it as a kind of one-form: the exterior derivative
of the function. In non-standard calculus
, differentials are regarded as infinitesimals, which can themselves be put on a rigorous footing (see differential (infinitesimal)).
One or both of the arguments may be suppressed, i.e., one may see df(x) or simply df. If y = ƒ(x), the differential may also be written as dy. Since dx(x, Δx) = Δx it is conventional to write dx = Δx, so that the following equality holds:
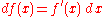
This notion of differential is broadly applicable when a linear approximation
to a function is sought, in which the value of the increment Δx is small enough. More precisely, if ƒ is a differentiable function
at x, then the difference in y-values
satisfies
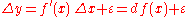
where the error ε in the approximation satisfies ε/Δx → 0 as Δx → 0. In other words, one has the approximate identity
in which the error can be made as small as desired relative to Δx by constraining Δx to be sufficiently small; that is to say,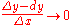
as Δx → 0. For this reason, the differential of a function is known as the principal (linear) part
in the increment of a function: the differential is a linear function
of the increment Δx, and although the error ε may be nonlinear, it tends to zero rapidly as Δx tends to zero.
the partial differential of y with respect to any one of the variables x1 is the principal part of the change in y resulting from a change dx1 in that one variable. The partial differential is therefore
involving the partial derivative
of y with respect to x1. The sum of the partial differentials with respect to all of the independent variables is the total differential
which is the principal part of the change in y resulting from changes in the independent variables x i.
More precisely, in the context of multivariable calculus, following , if ƒ is a differentiable function, then by the definition of the differentiability
, the increment
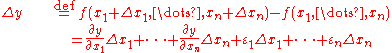
where the error terms ε i tend to zero as the increments Δxi jointly tend to zero. The total differential is then rigorously defined as
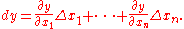
Since, with this definition,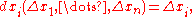
one has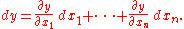
As in the case of one variable, the approximate identity holds
in which the total error can be made as small as desired relative to
by confining attention to sufficiently small increments.
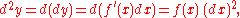
and, in general,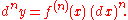
Informally, this justifies Leibniz's notation for higher-order derivatives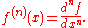
When the independent variable x itself is permitted to depend on other variables, then the expression becomes more complicated, as it must include also higher order differentials in x itself. Thus, for instance,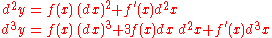
and so forth.
Similar considerations apply to defining higher order differentials of functions of several variables. For example, if ƒ is a function of two variables x and y, then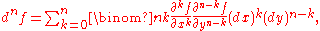
where
is a binomial coefficient
. In more variables, an analogous expression holds, but with an appropriate multinomial expansion rather than binomial expansion.
Higher order differentials in several variables also become more complicated when the independent variables are themselves allowed to depend on other variables. For instance, for a function ƒ of x and y which are allowed to depend on auxiliary variables, one has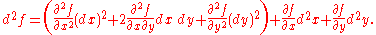
Because of this notational infelicity, the use of higher order differentials was roundly criticized by , who concluded:
That is: Finally, what is meant, or represented, by the equality [...]? In my opinion, nothing at all. In spite of this skepticism, higher order differentials did emerge as an important tool in analysis
In these contexts, the nth order differential of the function ƒ applied to an increment Δx is defined by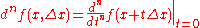
or an equivalent expression, such as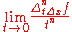
where
is an nth forward difference with increment tΔx.
This definition makes sense as well if ƒ is a function of several variables (for simplicity taken here as a vector argument). Then the nth differential defined in this way is a homogeneous function
of degree n in the vector increment Δx. Furthermore, the Taylor series
of ƒ at the point x is given by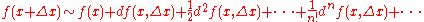
The higher order Gâteaux derivative
generalizes these considerations to infinite dimensional spaces.
An operation d with these two properties is known in abstract algebra
as a derivation
. In addition, various forms of the chain rule
hold, in increasing level of generality:
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the differential represents the principal part of the change in a function y = ƒ(x) with respect to changes in the independent variable. The differential dy is defined by
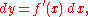
where
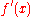is the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of ƒ with respect to x, and dx is an additional real variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
(so that dy is a function of x and dx). The notation is such that the equation
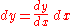
holds, where the derivative is represented in the Leibniz notation
Leibniz notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent "infinitely small" increments of x and y, just as Δx and Δy represent finite increments of x and y...
dy/dx, and this is consistent with regarding the derivative as the quotient of the differentials. One also writes
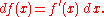
The precise meaning of the variables dy and dx depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
, or analytical significance if the differential is regarded as a linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
to the increment of a function. In physical applications, the variables dx and dy are often constrained to be very small ("infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
").
History and usage
The differential was first introduced via an intuitive or heuristic definition by Gottfried Wilhelm Leibniz, who thought of the differential dy as an infinitely small (or infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
) change in the value y of the function, corresponding to an infinitely small change dx in the function's argument x. For that reason, the instantaneous rate of change of y with respect to x, which is the value of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the function, is denoted by the fraction
in what is called the Leibniz notation
Leibniz notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent "infinitely small" increments of x and y, just as Δx and Δy represent finite increments of x and y...
for derivatives. The quotient dy/dx is not infinitely small; rather it is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
The use of infinitesimals in this form was widely criticized, for instance by the famous pamphlet The Analyst
The Analyst
The Analyst, subtitled "A DISCOURSE Addressed to an Infidel MATHEMATICIAN. WHEREIN It is examined whether the Object, Principles, and Inferences of the modern Analysis are more distinctly conceived, or more evidently deduced, than Religious Mysteries and Points of Faith", is a book published by...
by Bishop Berkeley. Augustin-Louis Cauchy (1823) defined the differential without appeal to the atomism of Leibniz's infinitesimals. Instead, Cauchy, following d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
, inverted the logical order of Leibniz and his successors: the derivative itself became the fundamental object, defined as a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of difference quotients, and the differentials were then defined in terms of it. That is, one was free to define the differential dy by an expression
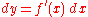
in which dy and dx are simply new variables taking finite real values, not fixed infinitesimals as they had been for Leibniz.
According to , Cauchy's approach was a significant logical improvement over the infinitesimal approach of Leibniz because, instead of invoking the metaphysical notion of infinitesimals, the quantities dy and dx could now be manipulated in exactly the same manner as any other real quantities
in a meaningful way. Cauchy's overall conceptual approach to differentials remains the standard one in modern analytical treatments, although the final word on rigor, a fully modern notion of the limit, was ultimately due to Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
.
In physical treatments, such as those applied to the theory of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, the infinitesimal view still prevails. reconcile the physical use of infinitesimal differentials with the mathematical impossibility of them as follows. The differentials represent finite non-zero values that are smaller than the degree of accuracy required for the particular purpose for which they are intended. Thus "physical infinitesimals" need not appeal to a corresponding mathematical infinitesimal in order to have a precise sense.
Following twentieth-century developments in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and differential geometry, it became clear that the notion of the differential of a function could be extended in a variety of ways. In real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, it is more desirable to deal directly with the differential as the principal part of the increment of a function. This leads directly to the notion that the differential of a function at a point is linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
of an increment Δx. This approach allows the differential (as a linear map) to be developed for a variety of more sophisticated spaces, ultimately giving rise to such notions as the Fréchet
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
or Gâteaux derivative
Gâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
. Likewise, in differential geometry, the differential of a function at a point is a linear function of a tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
(an "infinitely small displacement"), which exhibits it as a kind of one-form: the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of the function. In non-standard calculus
Non-standard calculus
In mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
, differentials are regarded as infinitesimals, which can themselves be put on a rigorous footing (see differential (infinitesimal)).
Definition
The differential is defined in modern treatments of differential calculus as follows. The differential of a function ƒ(x) of a single real variable x is the function df of two independent real variables x and Δx given byOne or both of the arguments may be suppressed, i.e., one may see df(x) or simply df. If y = ƒ(x), the differential may also be written as dy. Since dx(x, Δx) = Δx it is conventional to write dx = Δx, so that the following equality holds:
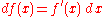
This notion of differential is broadly applicable when a linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
to a function is sought, in which the value of the increment Δx is small enough. More precisely, if ƒ is a differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
at x, then the difference in y-values
satisfies
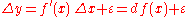
where the error ε in the approximation satisfies ε/Δx → 0 as Δx → 0. In other words, one has the approximate identity
in which the error can be made as small as desired relative to Δx by constraining Δx to be sufficiently small; that is to say,
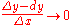
as Δx → 0. For this reason, the differential of a function is known as the principal (linear) part
Principal part
In mathematics, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series of a function.-Laurent series definition:...
in the increment of a function: the differential is a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
of the increment Δx, and although the error ε may be nonlinear, it tends to zero rapidly as Δx tends to zero.
Differentials in several variables
Following , for functions of more than one independent variable,
the partial differential of y with respect to any one of the variables x1 is the principal part of the change in y resulting from a change dx1 in that one variable. The partial differential is therefore
involving the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of y with respect to x1. The sum of the partial differentials with respect to all of the independent variables is the total differential
which is the principal part of the change in y resulting from changes in the independent variables x i.
More precisely, in the context of multivariable calculus, following , if ƒ is a differentiable function, then by the definition of the differentiability
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
, the increment
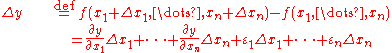
where the error terms ε i tend to zero as the increments Δxi jointly tend to zero. The total differential is then rigorously defined as
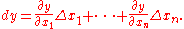
Since, with this definition,
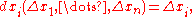
one has
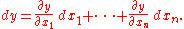
As in the case of one variable, the approximate identity holds
in which the total error can be made as small as desired relative to
by confining attention to sufficiently small increments.Higher-order differentials
Higher-order differentials of a function y = ƒ(x) of a single variable x can be defined via: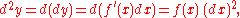and, in general,
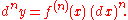
Informally, this justifies Leibniz's notation for higher-order derivatives
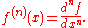
When the independent variable x itself is permitted to depend on other variables, then the expression becomes more complicated, as it must include also higher order differentials in x itself. Thus, for instance,
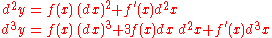
and so forth.
Similar considerations apply to defining higher order differentials of functions of several variables. For example, if ƒ is a function of two variables x and y, then
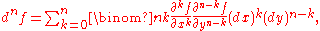
where
is a binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. In more variables, an analogous expression holds, but with an appropriate multinomial expansion rather than binomial expansion.
Higher order differentials in several variables also become more complicated when the independent variables are themselves allowed to depend on other variables. For instance, for a function ƒ of x and y which are allowed to depend on auxiliary variables, one has
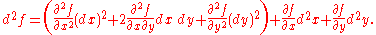
Because of this notational infelicity, the use of higher order differentials was roundly criticized by , who concluded:
- Enfin, que signifie ou que représente l'égalité
- A mon avis, rien du tout.
That is: Finally, what is meant, or represented, by the equality [...]? In my opinion, nothing at all. In spite of this skepticism, higher order differentials did emerge as an important tool in analysis
In these contexts, the nth order differential of the function ƒ applied to an increment Δx is defined by
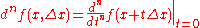
or an equivalent expression, such as
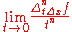
where
is an nth forward difference with increment tΔx.This definition makes sense as well if ƒ is a function of several variables (for simplicity taken here as a vector argument). Then the nth differential defined in this way is a homogeneous function
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree n in the vector increment Δx. Furthermore, the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of ƒ at the point x is given by
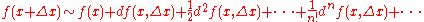
The higher order Gâteaux derivative
Gâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
generalizes these considerations to infinite dimensional spaces.
Properties
A number of properties of the differential follow in a straightforward manner from the corresponding properties of the derivative, partial derivative, and total derivative. These include:- Linearity: For constants a and b and differentiable functions ƒ and g,
-
- Product ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
: For two differentiable functions ƒ and g,
- Product rule
An operation d with these two properties is known in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
as a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
. In addition, various forms of the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
hold, in increasing level of generality:
- If y = ƒ(u) is a differentiable function of the variable u and u = g(x) is a differentiable function of x, then
- If y = ƒ(x1, ..., xn) and all of the variables x1, ..., xn depend on another variable t, then by the chain rule for partial derivatives, one has
-
-
- Heuristically, the chain rule for several variables can itself be understood by dividing through both sides of this equation by the infinitely small quantity dt.
- More general analogous expressions hold, in which the intermediate variables x i depend on more than one variable.
General formulation
A consistent notion of differential can be developed for a function ƒ Rn → Rm between two Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s. Let x,Δx ∈ Rn be a pair of Euclidean vectors. The increment in the function ƒ is
If there exists an m × n matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A such that
in which the vector ε → 0 as Δx → 0, then ƒ is by definition differentiable at the point x. The matrix A is sometimes known as the Jacobian matrix, and the linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
that associates to the increment Δx ∈ Rn the vector AΔx ∈ Rm is, in this general setting, known as the differential dƒ(x) of ƒ at the point x. This is precisely the Fréchet derivativeFréchet derivativeIn mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
, and the same construction can be made to work for a function between any Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.
Another fruitful point of view is to define the differential directly as a kind of directional derivativeDirectional derivativeIn mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
:
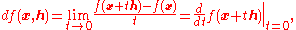
which is the approach already taken for defining higher order differentials (and is most nearly the definition set forth by Cauchy). If t represents time and x position, then h represents a velocity instead of a displacement as we have heretofore regarded it. This yields yet another refinement of the notion of differential: that it should be a linear function of a kinematic velocity. The set of all velocities through a given point of space is known as the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
, and so dƒ gives a linear function on the tangent space: a differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
. With this interpretation, the differential of ƒ is known as the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, and has broad application in differential geometry because the notion of velocities and the tangent space makes sense on any differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
. If, in addition, the output value of ƒ also represents a position (in a Euclidean space), then a dimensional analysis confirms that the output value of dƒ must be a velocity. If one treats the differential in this manner, then it is known as the pushforward since it "pushes" velocities from a source space into velocities in a target space.
Other approaches
Although the notion of having an infinitesimal increment dx is not well-defined in modern mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a variety of techniques exist for defining the infinitesimal differential so that the differential of a function can be handled in a manner that does not clash with the Leibniz notationLeibniz notationIn calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent "infinitely small" increments of x and y, just as Δx and Δy represent finite increments of x and y...
. These include:
- Defining the differential as a kind of differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
, specifically the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of a function. The infinitesimal increments are then identified with vectors in the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at a point. This approach is popular in differential geometry and related fields, because it readily generalizes to mappings between differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s. - Differentials as nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements of commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s. This approach is popular in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. - Differentials in smooth models of set theory. This approach is known as synthetic differential geometrySynthetic differential geometryIn mathematics, synthetic differential geometry is a reformulation of differential geometry in the language of topos theory, in the context of an intuitionistic logic characterized by a rejection of the law of excluded middle. There are several insights that allow for such a reformulation...
or smooth infinitesimal analysisSmooth infinitesimal analysisSmooth infinitesimal analysis is a mathematically rigorous reformulation of the calculus in terms of infinitesimals. Based on the ideas of F. W. Lawvere and employing the methods of category theory, it views all functions as being continuous and incapable of being expressed in terms of discrete...
and is closely related to the algebraic geometric approach, except that ideas from topos theory are used to hide the mechanisms by which nilpotent infinitesimals are introduced. - Differentials as infinitesimals in hyperreal numberHyperreal numberThe system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
systems, which are extensions of the real numbers which contain invertible infinitesimals and infinitely large numbers. This is the approach of nonstandard analysis pioneered by Abraham RobinsonAbraham RobinsonAbraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
.
Examples and applications
Differentials may be effectively used in numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
to study the propagation of experimental errors in a calculation, and thus the overall numerical stabilityNumerical stabilityIn the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
of a problem . Suppose that the variable x represents the outcome of an experiment and y is the result of a numerical computation applied to x. The question is to what extent errors in the measurement of x influence the outcome of the computation of y. If the x is known to within Δx of its true value, then Taylor's theoremTaylor's theoremIn calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
gives the following estimate on the error Δy in the computation of y:
where ξ = x + θΔx for some 0 < θ < 1. If Δx is small, then the second order term is negligible, so that Δy is, for practical purposes, well-approximated by dy = ƒ(x)Δx.
The differential is often useful to rewrite a differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
in the form
in particular when one wants to separate the variablesSeparation of variablesIn mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
.
External links
- Differential Of A Function at Wolfram Demonstrations Project
-
