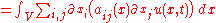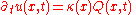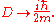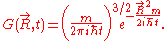Heat equation
Encyclopedia

Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
which describes the distribution of heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
(or variation in temperature) in a given region over time. For a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
u(x,y,z,t) of three spatial variables (x,y,z) and the time variable t, the heat equation is
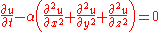
also written

or sometimes
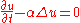
where
 is a positive constant and
is a positive constant and  or
or 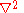 denotes the Laplace operator
denotes the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. In the physical problem of temperature variation, u(x,y,z,t) is the temperature and
 is the thermal diffusivity
is the thermal diffusivityThermal diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
. For the mathematical treatment it is sufficient to consider the case α = 1.
The heat equation is of fundamental importance in diverse scientific fields. In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it is the prototypical parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
. In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the heat equation is connected with the study of Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
via the Fokker–Planck equation. In financial mathematics it is used to solve the Black–Scholes partial differential equation. The diffusion equation, a more general version of the heat equation, arises in connection with the study of chemical diffusion and other related processes.
General description
Suppose one has a function u which describes the temperature at a given location (x, y, z). This function will change over time as heat spreads throughout space. The heat equation is used to determine the change in the function u over time. The image to the right is animated and describes the way heat changes in time along a metal bar. One of the interesting properties of the heat equation is the maximum principleMaximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
which says that the maximum value of u is either earlier in time than the region of concern or on the edge of the region of concern. This is essentially saying that temperature comes either from some source or from earlier in time because heat permeates but is not created from nothingness. This is a property of parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s and is not difficult to prove mathematically (see below).
Another interesting property is that even if u has a discontinuity at an initial time t = t0, the temperature becomes smooth as soon as t > t0. For example, if a bar of metal has temperature 0 and another has temperature 100 and they are stuck together end to end, then very quickly the temperature at the point of connection is 50 and the graph of the temperature is smoothly running from 0 to 100.
The heat equation is used in probability and describes random walks. It is also applied in financial mathematics for this reason.
It is also important in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and thus topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
: it was adapted by Richard Hamilton
Richard Hamilton (professor)
Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
when he defined the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
that was later used by Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
to solve the topological Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
.
Derivation in one dimension
The heat equation is derived from Fourier's law and conservation of energyConservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
.
By Fourier's law, the flow rate of heat energy through a surface is proportional to the negative temperature gradient across the surface,

where k is the thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
and u is the temperature. In one dimension, the gradient is an ordinary spatial derivative, and so Fourier's law is
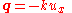
where ux is ∂u/∂x. In the absence of work done, a change in internal energy per unit volume in the material, ΔQ, is proportional to the change in temperature, Δu. That is,
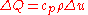
where cp is the specific heat capacity and ρ is the mass density of the material. (In this section only, Δ is the ordinary difference operator, not the Laplacian.) Choosing zero energy at absolute zero temperature, this can be rewritten as
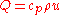 .
.The increase in internal energy in a small spatial region of the material

over the time period

is given by

where the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
was used. If no work is done and there are neither heat sources nor sinks, the change in internal energy in the interval [x-Δx, x+Δx] is accounted for entirely by the flux of heat across the boundaries. By Fourier's law, this is
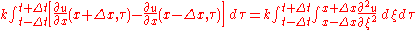
again by the fundamental theorem of calculus. By conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
,
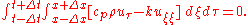
This is true for any rectangle [t−Δt, t+Δt] × [x−Δx, x+Δx]. Consequently, the integrand must vanish identically:
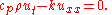
Which can be rewritten as:
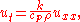
or:
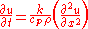
which is the heat equation. The coefficient k/(cpρ) is called thermal diffusivity
Thermal diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
and is often denoted α.
Three-dimensional problem
In the special cases of wave propagationWave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
of heat in an isotropic and homogeneous medium in a 3-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al space, this equation is
-

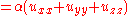
where:
- u = u(x, y, z, t) is temperature as a function of space and time;
-
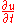 is the rate of change of temperature at a point over time;
is the rate of change of temperature at a point over time;
- uxx, uyy, and uzz are the second spatial derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s (thermal conductions) of temperature in the x, y, and z directions, respectively;
-
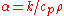 is the thermal diffusivityThermal diffusivityIn heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
is the thermal diffusivityThermal diffusivityIn heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
, a material-specific quantity depending on the thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
, k, the mass density,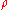 , and the specific heat capacity,
, and the specific heat capacity,  .
.
The heat equation is a consequence of Fourier's law of cooling (see heat conductionHeat conductionIn heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
).
If the medium is not the whole space, in order to solve the heat equation uniquely we also need to specify boundary conditions for u. To determine uniqueness of solutions in the whole space it is necessary to assume an exponential bound on the growth of solutions; this assumption is consistent with observed experiments.
Solutions of the heat equation are characterized by a gradual smoothing of the initial temperature distribution by the flow of heatHeatIn physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
from warmer to colder areas of an object. Generally, many different states and starting conditions will tend toward the same stable equilibriumThermodynamic equilibriumIn thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
. As a consequence, to reverse the solution and conclude something about earlier times or initial conditions from the present heat distribution is very inaccurate except over the shortest of time periods.
The heat equation is the prototypical example of a parabolic partial differential equationParabolic partial differential equationA parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
.
Using the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, the heat equation can be simplified, and generalized to similar equations over spaces of arbitrary number of dimensions, as
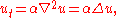
where the Laplace operator, Δ or , the divergence of the gradient, is taken in the spatial variables.
, the divergence of the gradient, is taken in the spatial variables.
The heat equation governs heat diffusion, as well as other diffusive processes, such as particle diffusion or the propagation of action potentialAction potentialIn physiology, an action potential is a short-lasting event in which the electrical membrane potential of a cell rapidly rises and falls, following a consistent trajectory. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and...
in nerve cells. Although they are not diffusive in nature, some quantum mechanics problems are also governed by a mathematical analog of the heat equation (see below). It also can be used to model some phenomena arising in financeFinance"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, like the Black–Scholes or the Ornstein-Uhlenbeck processOrnstein-Uhlenbeck processIn mathematics, the Ornstein–Uhlenbeck process , is a stochastic process that, roughly speaking, describes the velocity of a massive Brownian particle under the influence of friction...
es. The equation, and various non-linear analogues, has also been used in image analysis.
The heat equation is, technically, in violation of special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, because its solutions involve instantaneous propagation of a disturbance. The part of the disturbance outside the forward light coneLight coneA light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
can usually be safely neglected, but if it is necessary to develop a reasonable speed for the transmission of heat, a hyperbolic problemHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
should be considered instead – like a partial differential equation involving a second-order time derivative. Some models of nonlinear heat conduction (which are also parabolic equations) have solutions with finite heat transmission speed.
Internal heat generation
The function u above represents temperature of a body. Alternatively, it is sometimes convenient to change units and represent u as the heat densityHeat fluxHeat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
of a medium. Since heat density is proportional to temperature in a homogeneous medium, the heat equation is still obeyed in the new units.
Suppose that a body obeys the heat equation and, in addition, generates its own heat per unit volume (e.g., in watts/L) at a rate given by a known function q varying in space and time. Then the heat per unit volume u satisfies an equation
-
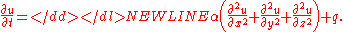
For example, a tungsten light bulb filament generates heat, so it would have a positive nonzero value for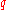 when turned on. While the light is turned off, the value of
when turned on. While the light is turned off, the value of 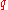 for the tungsten filament would be zero.
for the tungsten filament would be zero.
Solving the heat equation using Fourier series
The following solution technique for the heat equation was proposed by Joseph FourierJoseph FourierJean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
in his treatise Théorie analytique de la chaleur, published in 1822. Let us consider the heat equation for one space variable. This could be used to model heat conduction in a rod. The equation is
where u = u(x, t) is a function of two variables x and t. Here- x is the space variable, so x ∈ [0,L], where L is the length of the rod.
- t is the time variable, so t ≥ 0.
We assume the initial condition
where the function f is given, and the boundary conditions
Let us attempt to find a solution of which is not identically zero satisfying the boundary conditions but with the following property: u is a product in which the dependence of u on x, t is separated, that is:
This solution technique is called separation of variablesSeparation of variablesIn mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. Substituting u back into equation ,
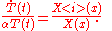
Since the right hand side depends only on x and the left hand side only on t, both sides are equal to some constant value −λ. Thus:
and
We will now show that nontrivial solutions for for values of λ ≤ 0 cannot occur:
Suppose that λ < 0. Then there exist real numbers B, C such that
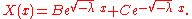
From we get
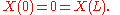
and therefore B = 0 = C which implies u is identically 0.
Suppose that λ = 0. Then there exist real numbers B, C such that
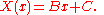
From equation we conclude in the same manner as in 1 that u is identically 0.
Therefore, it must be the case that λ > 0. Then there exist real numbers A, B, C such that
and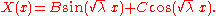
From we get C = 0 and that for some positive integer n,
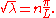
This solves the heat equation in the special case that the dependence of u has the special form .
In general, the sum of solutions to which satisfy the boundary conditions also satisfies and . We can show that the solution to , and is given by

where

Generalizing the solution technique
The solution technique used above can be greatly extended to many other types of equations. The idea is that the operator uxx with the zero boundary conditions can be represented in terms of its eigenvectors. This leads naturally to one of the basic ideas of the spectral theorySpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of linear self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s.
Consider the linear operator Δ u = ux x. The infinite sequence of functions
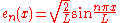
for n ≥ 1 are eigenvectors of Δ. Indeed
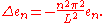
Moreover, any eigenvector f of Δ with the boundary conditions f(0)=f(L)=0 is of the form en for some n ≥ 1. The functions en for n ≥ 1 form an orthonormal sequence with respect to a certain inner product on the space of real-valued functions on [0, L]. This means

Finally, the sequence {en}n ∈ N spans a dense linear subspace of L2(0, L). This shows that in effect we have diagonalizedDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
the operator Δ.
Heat conduction in non-homogeneous anisotropic media
In general, the study of heat conduction is based on several principles. Heat flow is a form of energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
flow, and as such it is meaningful to speak of the time rate of flow of heat into a region of space.
- The time rate of heat flow into a region V is given by a time-dependent quantity qt(V). We assume q has a densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, so that
- Heat flow is a time-dependent vector function H(x) characterized as follows: the time rate of heat flowing through an infinitesimal surface element with area d S and with unit normal vector n is
Thus the rate of heat flow into V is also given by the surface integral

where n(x) is the outward pointing normal vector at x.
- The Fourier law states that heat energy flow has the following linear dependence on the temperature gradient
- where A(x) is a 3 × 3 real matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that is symmetric and positive definitePositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
.
By Green's theoremGreen's theoremIn mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
, the previous surface integral for heat flow into V can be transformed into the volume integral

- The time rate of temperature change at x is proportional to the heat flowing into an infinitesimal volume element, where the constant of proportionality is dependent on a constant κ
Putting these equations together gives the general equation of heat flow:
Remarks.
- The coefficient κ(x) is the inverse of specific heat of the substance at x × densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the substance at x.
- In the case of an isotropic medium, the matrix A is a scalar matrix equal to thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
.
- In the anisotropic case where the coefficient matrix A is not scalar (i.e., if it depends on x), then an explicit formula for the solution of the heat equation can seldom be written down. Though, it is usually possible to consider the associated abstract Cauchy problemCauchy problemA Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
and show that it is a well-posed problemWell-posed problemThe mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
and/or to show some qualitative properties (like preservation of positive initial data, infinite speed of propagation, convergence toward an equilibrium, smoothing properties). This is usually done by one-parameter semigroups theory: for instance, if A is a symmetric matrix, then the elliptic operatorElliptic operatorIn the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
defined by
- is self-adjointSelf-adjointIn mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
and dissipative, thus by the spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
it generates a one-parameter semigroup.
Fundamental solutions
A fundamental solutionFundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
, also called a heat kernel, is a solution of the heat equation corresponding to the initial condition of an initial point source of heat at a known position. These can be used to find a general solution of the heat equation over certain domains; see, for instance, for an introductory treatment.
In one variable, the Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
is a solution of the initial value problem
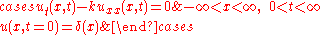
where δ is the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. The solution to this problem is the fundamental solution

One can obtain the general solution of the one variable heat equation with initial condition u(x,0) = g(x) for -∞<x<∞ and 0<t<∞ by applying a convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
:
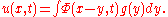
In several spatial variables, the fundamental solution solves the analogous problem

in -∞<xi<∞, i=1,...,n, and 0<t<∞. The n-variable fundamental solution is the product of the fundamental solutions in each variable; i.e.,
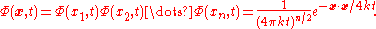
The general solution of the heat equation on Rn is then obtained by a convolution, so that to solve the initial value problem with u(x,t=0)=g(x), one has
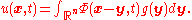
The general problem on a domain Ω in Rn is

with either DirichletDirichlet problemIn mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
or Neumann boundary data. A Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
always exists, but unless the domain Ω can be readily decomposed into one-variable problems (see below), it may not be possible to write it down explicitly. The method of imagesMethod of imagesSee also Method of image charges for applications in electrostatics and magnetostaticsMethod of images is a mathematical tool for solving differential equations in which the domain of the sought function is extended by the addition of its mirror image with respect to a symmetry hyperplane, with...
provides one additional technique for obtaining Green's functions for non-trivial domains.
Some Green's function solutions in 1D
A variety of elementary Green's function solutions in one-dimension are recorded here. In some of these, the spatial domain is the entire real line (-∞,∞). In others, it is the semi-infinite interval (0,∞) with either Neumann or DirichletDirichlet problemIn mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
boundary conditions. One further variation is that some of these solve the inhomogeneous equation
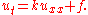
where f is some given function of x and t.
Homogeneous heat equation
Initial value problem on (-∞,∞)
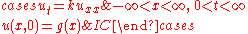

- Comment. This solution is the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with respect to the variable of the fundamental solution
of the fundamental solution  and the function
and the function 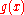 . Therefore, according to the general properties of the convolution with respect to differentiation,
. Therefore, according to the general properties of the convolution with respect to differentiation,  is a solution of the same heat equation, for
is a solution of the same heat equation, for 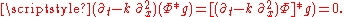 Moreover,
Moreover,  and
and 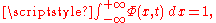 so that, by general facts about approximation to the identityMollifierIn mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
so that, by general facts about approximation to the identityMollifierIn mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
,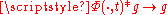 as
as 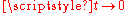 in various senses, according to the specific
in various senses, according to the specific 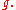 For instance, if
For instance, if  is assumed bounded and continuous on
is assumed bounded and continuous on  then
then  converges uniformly to
converges uniformly to 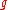 as
as 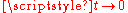 , meaning that
, meaning that 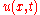 is continuous on
is continuous on 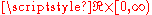 with
with 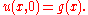
Initial value problem on (0,∞) with homogeneous Dirichlet boundary conditions
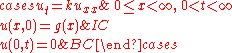
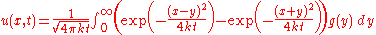
- Comment. This solution is obtained from the preceding formula as applied to the data
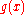 suitably extended to
suitably extended to 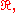 so as to be an odd function, that is, letting
so as to be an odd function, that is, letting 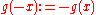 for all
for all  Correspondingly, the solution of the initial value problem on
Correspondingly, the solution of the initial value problem on 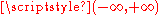 is an odd function with respect to the variable
is an odd function with respect to the variable  for all values of
for all values of  and in particular it satisfies the homogeneous Dirichlet boundary conditions
and in particular it satisfies the homogeneous Dirichlet boundary conditions 
Initial value problem on (0,∞) with homogeneous Neumann boundary conditions
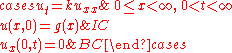

- Comment. This solution is obtained from the first solution formula as applied to the data
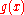 suitably extended to
suitably extended to 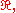 so as to be an even function, that is, letting
so as to be an even function, that is, letting  for all
for all  Correspondingly, the solution of the initial value problem on
Correspondingly, the solution of the initial value problem on 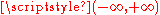 is an even function with respect to the variable
is an even function with respect to the variable  for all values of
for all values of  and in particular, being smooth, it satisfies the homogeneous Neumann boundary conditions
and in particular, being smooth, it satisfies the homogeneous Neumann boundary conditions 
Problem on (0,∞) with homogeneous initial conditions and non-homogeneous Dirichlet boundary conditions
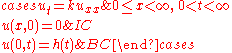

- Comment. This solution is the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with respect to the variable of
of  and the function
and the function 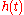 . Since
. Since 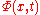 is the fundamental solution of
is the fundamental solution of  the function
the function 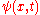 is also a solution of the same heat equation, and so is
is also a solution of the same heat equation, and so is  , thanks to general properties of the convolution with respect to differentiation. Moreover,
, thanks to general properties of the convolution with respect to differentiation. Moreover, 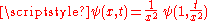 and
and  so that, by general facts about approximation to the identityMollifierIn mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
so that, by general facts about approximation to the identityMollifierIn mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
,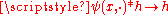 as
as 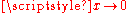 in various senses, according to the specific
in various senses, according to the specific  For instance, if
For instance, if 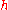 is assumed continuous on
is assumed continuous on  with support in
with support in 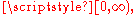 then
then 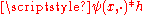 converges uniformly on compacta to
converges uniformly on compacta to  as
as  , meaning that
, meaning that  is continuous on
is continuous on 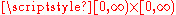 with
with 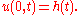
Inhomogeneous heat equation
Problem on (-∞,∞) homogeneous initial conditions
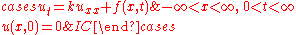
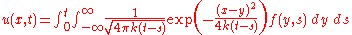
Comment. This solution is the convolution in , that is with respect to both the variables
, that is with respect to both the variables  and
and  of the fundamental solution
of the fundamental solution  and the function
and the function  both meant as defined on the whole
both meant as defined on the whole 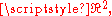 and identically 0 for all
and identically 0 for all  . One verifies that
. One verifies that 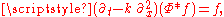 which is expressed in the language of distributions as
which is expressed in the language of distributions as 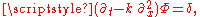 where the distribution
where the distribution  is the Dirac's delta function, that is the evaluation at 0.
is the Dirac's delta function, that is the evaluation at 0.
Problem on (0,∞) with homogeneous Dirichlet boundary conditions and initial conditions
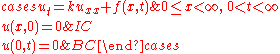
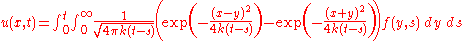
Comment. This solution is obtained from the preceding formula as applied to the data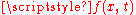 suitably extended to
suitably extended to  , so as to be an odd function of the variable
, so as to be an odd function of the variable 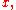 that is, letting
that is, letting  for all
for all  and
and  Correspondingly, the solution of the inhomogeneous problem on
Correspondingly, the solution of the inhomogeneous problem on 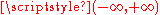 is an odd function with respect to the variable
is an odd function with respect to the variable  for all values of
for all values of  and in particular it satisfies the homogeneous Dirichlet boundary conditions
and in particular it satisfies the homogeneous Dirichlet boundary conditions 
Problem on (0,∞) with homogeneous Neumann boundary conditions and initial conditions
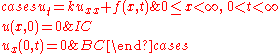

Comment. This solution is obtained from the first formula as applied to the data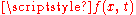 suitably extended to
suitably extended to 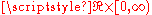 , so as to be an even function of the variable
, so as to be an even function of the variable  that is, letting
that is, letting 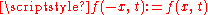 for all
for all  and
and  Correspondingly, the solution of the inhomogeneous problem on
Correspondingly, the solution of the inhomogeneous problem on  is an even function with respect to the variable
is an even function with respect to the variable  for all values of
for all values of  and in particular, being a smooth function, it satisfies the homogeneous Neumann boundary conditions
and in particular, being a smooth function, it satisfies the homogeneous Neumann boundary conditions 
Examples
Since the heat equation is linear, solutions of other combinations of boundary conditions, inhomogeneous term, and initial conditions can be found by taking an appropriate linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the above Green's function solutions.
For example, to solve
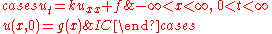
let
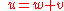
where u and v solve the problems
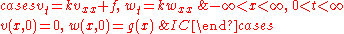
Similarly, to solve
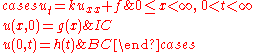
let

where w, v, and r solve the problems

Mean-value property for the heat equation
Solutions of the heat equations satisfy a mean-value property analogous to the mean-value properties of harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
satisfy a mean-value property analogous to the mean-value properties of harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s (solutions of ), though a bit more complicated. Precisely, if
), though a bit more complicated. Precisely, if  solves
solves  and
and  then
then
where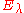 is a "heat-ball", that is a super-level set of the fundamental solution of the heat equation:
is a "heat-ball", that is a super-level set of the fundamental solution of the heat equation:
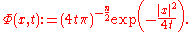
Notice that as
as  so the above formula holds for any
so the above formula holds for any 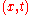 in the (open) set
in the (open) set  for
for 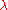 large enough. Conversely, any function u satisfying the above mean-value property on an open domain of
large enough. Conversely, any function u satisfying the above mean-value property on an open domain of  is a solution of the heat equation. This can be shown by an argument similar to the analogous one for harmonic functions.
is a solution of the heat equation. This can be shown by an argument similar to the analogous one for harmonic functions.
Stationary Heat Equation
The stationary heat equation is not dependent on time. This happens in all those problems, where the time equilibrium constant is fast enough to approximate the more complex time dependent heat equation to the stationary case. This equation is much simpler and can help to understand better the physics of the materials without focusing on the dynamic of the heat transport process. It is widely used for simple engineering problems assuming there is equilibrium with time.
Stationary condition:
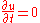
Stationary heat equation with heat source (inhomogeneous case), which is also Poisson's equationPoisson's equationIn mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
:

Stationary heat equation without heat source (homogeneous case), which is also Laplace's equationLaplace's equationIn mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
:
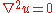
where is the temperatureThermodynamic temperatureThermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
is the temperatureThermodynamic temperatureThermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
, is the thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
is the thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
and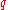 the heat source density.
the heat source density.
Particle diffusion
One can model particle diffusionDiffusionMolecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
by an equation involving either:- the volumetric concentrationConcentrationIn chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
of particles, denoted c, in the case of collective diffusion of a large number of particles, or - the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
associated with the position of a single particle, denoted P.
In either case, one uses the heat equation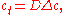
or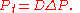
Both c and P are functions of position and time. D is the diffusion coefficient that controls the speed of the diffusive process, and is typically expressed in meters squared over second. If the diffusion coefficient D is not constant, but depends on the concentration c (or P in the second case), then one gets the nonlinear diffusion equation.
Brownian motion
The random trajectory of a single particle subject to the particle diffusion equation (or heat equation) is a Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
. If a particle is placed at at time
at time  , then the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, then the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
associated with the position vector of the particle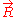 will be the following:
will be the following:
which is a (multivariate) normal distribution evolving in time.
Schrödinger equation for a free particle
With a simple division, the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for a single particle of massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
m in the absence of any applied force field can be rewritten in the following way: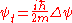 , where i is the unit imaginary numberImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, where i is the unit imaginary numberImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, and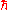 is Planck's constant divided by
is Planck's constant divided by  , and
, and 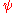 is the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
is the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of the particle.
This equation is formally similar to the particle diffusion equation, which one obtains through the following transformation: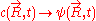
Applying this transformation to the expressions of the Green functions determined in the case of particle diffusion yields the Green functions of the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, which in turn can be used to obtain the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
at any time through an integral on the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
at t=0:-
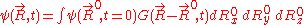 , with
, with
-
Remark: this analogy between quantum mechanics and diffusion is a purely formal one. Physically, the evolution of the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
satisfying Schrödinger's equation might have an origin other than diffusion.
Thermal diffusivity in polymers
A direct practical application of the heat equation, in conjunction with Fourier theory, in spherical coordinates, is the measurement of the thermal diffusivity in polymers (Unsworth and DuarteF. J. DuarteF. J. Duarte is a laser physicist and author/editor of several well-known books on tunable lasers. He introduced the generalized multiple-prism dispersion theory and has discovered various multiple-prism grating oscillator laser configurations...
). The dual theoretical-experimental method demonstrated by these authors is applicable to rubber and various other materials of practical interest.
Further applications
The heat equation arises in the modelingMathematical modelA mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of a number of phenomena and is often used in financial mathematics in the modeling of optionsOption (finance)In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
. The famous Black–Scholes option pricing model's differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
can be transformed into the heat equation allowing relatively easy solutions from a familiar body of mathematics. Many of the extensions to the simple option models do not have closed form solutions and thus must be solved numerically to obtain a modeled option price.
The equation describing pressure diffusion in an porous medium is identical in form with the heat equation. Diffusion problems dealing with Dirichlet, NeumannNeumannNeumann may refer to:*Alfred Neumann, German writer*Alfred Neumann, East German politician*Bernd Neumann, German politician*Bernhard Neumann, German-born mathematician...
and RobinRobinRobin may refer to:* Robin , a common given name and a surname.It may also refer to:- Birds:Most birds called "robins" belong to the superfamily Muscicapoidea:* European Robin...
boundary conditions have closed form analytic solutions .
The heat equation is also widely used in image analysis and in machine-learning as the driving theory behind scale-spaceScale spaceScale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision...
or graph Laplacian methods. The heat equation can be efficiently solved numerically using the Crank–Nicolson method of . This method can be extended to many of the models with no closed form solution, see for instance .
An abstract form of heat equation on manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s provides a major approach to the Atiyah–Singer index theoremAtiyah–Singer index theoremIn differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
, and has led to much further work on heat equations in Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
.
External links
- Derivation of the heat equation
- Linear heat equations: Particular solutions and boundary value problems - from EqWorld