
Stationary point
Encyclopedia
- Not to be confused with a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
where x = f(x).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, a stationary point is an input to a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
where the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is zero (equivalently, the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
is zero): where the function "stops" increasing or decreasing (hence the name).
For the graph of a one-dimensional function, this corresponds to a point on the graph where the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
is parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to the x-axis. For the graph of a two-dimensional function, this corresponds to a point on the graph where the tangent plane is parallel to the xy plane.
The term is mostly used in two dimensions, which this article discusses: stationary points in higher dimensions are usually referred to as critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
; see there for higher dimensional discussion.
Stationary points, critical points and turning points
The term "critical point" may be confused with "stationary point".Critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
is more general: a critical point is either a stationary point or a point where the derivative is not defined. Thus A stationary point is always a critical point,
but a critical point is not always a stationary point: it might also be a non-differentiable point. For a smooth function, these are interchangeable, hence the confusion; when a function is understood to be smooth, one can refer to stationary points as critical points, but when it may be non-differentiable, one should distinguish these notions. There is also a different definition of critical point in higher dimensions, where the derivative does not have full rank, but is not necessarily zero; this is not analogous to stationary points, as the function may still be changing in some direction.
A turning point is a point at which the derivative changes sign. A turning point may be either a local maximum or a minimum point. If the function is smooth, then the turning point must be a stationary point, however not all stationary points are turning points, for example
 has a stationary point at x=0, but the derivative doesn't change sign as there is a point of inflexion at x=0.
has a stationary point at x=0, but the derivative doesn't change sign as there is a point of inflexion at x=0.Classification
Isolated stationary points of a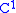 real valued function
real valued function  are classified into four kinds, by the first derivative test
are classified into four kinds, by the first derivative testFirst derivative test
In calculus, the first derivative test uses the first derivative of a function to determine whether a given critical point of a function is a local maximum, a local minimum, or neither.-Intuitive explanation:...
:
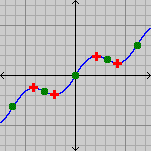
- a minimal extremum (minimal turning point or relative minimum) is one where the derivative of the function changes from negative to positive;
- a maximal extremum (maximal turning point or relative maximum) is one where the derivative of the function changes from positive to negative;
- a rising point of inflectionInflection pointIn differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
(or inflexion) is one where the derivative of the function is positive on both sides of the stationary point; such a point marks a change in concavityConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:... - a falling point of inflectionInflection pointIn differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
(or inflexion) is one where the derivative of the function is negative on both sides of the stationary point; such a point marks a change in concavity
Notice: Global (or absolute) maxima and minima are sometimes called global (or absolute) maximal (resp. minimal) extrema. By Fermat's theorem
Fermat's theorem (stationary points)
In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point...
, they must occur on the boundary or at critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s, but they do not necessarily occur at stationary points.
Curve sketching
Determining the position and nature of stationary points aids in curve sketchingCurve sketching
In geometry, curve sketching includes techniques that can used to produce a rough idea of overall shape of a plane curve given its equation without computing the large numbers of points required for a detailed plot...
, especially for continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s. Solving the equation f'(x) = 0 returns the x-coordinates of all stationary points; the y-coordinates are trivially the function values at those x-coordinates.
The specific nature of a stationary point at x can in some cases be determined by examining the second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
f''(x):
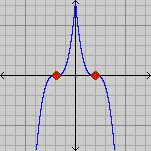
- If f''(x) < 0, the stationary point at x is concave down; a maximal extremum.
- If f''(x) > 0, the stationary point at x is concave up; a minimal extremum.
- If f''(x) = 0, the nature of the stationary point must be determined by way of other means, often by noting a sign change around that point provided the function values exist around that point.
A more straightforward way of determining the nature of a stationary point is by examining the function values between the stationary points. However, this is limited again in that it works only for functions that are continuous in at least a small interval surrounding the stationary point.
A simple example of a point of inflection is the function f(x) = x3. There is a clear change of concavity about the point x = 0, and we can prove this by means of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. The second derivative of f is the everywhere-continuous 6x, and at x = 0, f′′ = 0, and the sign changes about this point. So x = 0 is a point of inflection.
More generally, the stationary points of a real valued function f: Rn → R are those
points x0 where the derivative in every direction equals zero, or equivalently, the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is zero.
Example
At x1 we have f' (x) = 0 and f''(x) = 0. Even though f''(x) = 0, this point is not a point of inflexion. The reason is that the sign of f' (x) changes from negative to positive.At x2, we have f' (x)
 0 and f''(x) = 0. But, x2 is not a stationary point, rather it is a point of inflexion. This because the concavity changes from concave downwards to concave upwards and the sign of f' (x) does not change; it stays positive.
0 and f''(x) = 0. But, x2 is not a stationary point, rather it is a point of inflexion. This because the concavity changes from concave downwards to concave upwards and the sign of f' (x) does not change; it stays positive.At x3 we have f' (x) = 0 and f''(x) = 0. Here, x3 is both a stationary point and a point of inflexion. This is because the concavity changes from concave downwards to concave upwards and the sign of f' (x) does not change; it stays positive.
Assuming that f'(x) < 0, there are no distinct roots. Hence f
See also
- Optimization (mathematics)Optimization (mathematics)In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
- Fermat's theoremFermat's theorem (stationary points)In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point...
- Second derivative testSecond derivative testIn calculus, the second derivative test is a criterion often useful for determining whether a given stationary point of a function is a local maximum or a local minimum using the value of the second derivative at the point....
- Higher-order derivative test
- Fixed point (mathematics)Fixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
- Saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
External links
- Inflection Points of Fourth Degree Polynomials — a surprising appearance of the golden ratio at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

