Linearization
Encyclopedia
In mathematics
and its applications, linearization refers to finding the linear approximation
to a function
at a given point. In the study of dynamical system
s, linearization is a method for assessing the local stability
of an equilibrium point of a system
of nonlinear differential equation
s or discrete dynamical system
s. This method is used in fields such as engineering
, physics
, economics
, and ecology
.
are lines
— ones that are usually used for purposes of calculation. Linearization is an effective method for approximating the output of a function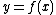 at any
at any  based on the value and slope
based on the value and slope
of the function at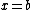 , given that f(x) is continuous on
, given that f(x) is continuous on  (or
(or 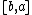 ) and that
) and that  is close to
is close to 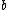 . In, short, linearization approximates the output of a function near
. In, short, linearization approximates the output of a function near  .
.
For example, you might know that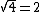 . However, without a calculator, what would be a good approximation of
. However, without a calculator, what would be a good approximation of 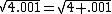 ?
?
For any given function ,
, 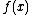 can be approximated if it is near a known continuous point. The most basic requisite is that, where
can be approximated if it is near a known continuous point. The most basic requisite is that, where 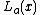 is the linearization of f(x) at x = a,
is the linearization of f(x) at x = a, 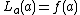 . The point-slope form of an equation forms an equation of a line, given a point
. The point-slope form of an equation forms an equation of a line, given a point 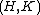 and slope
and slope  . The general form of this equation is:
. The general form of this equation is: 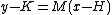 .
.
Using the point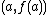 ,
, 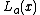 becomes
becomes 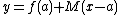 . Because continuous functions are locally linear
. Because continuous functions are locally linear
, the best slope to substitute in would be the slope of the line tangent
to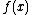 at
at  .
.
While the concept of local linearity applies the most to points arbitrarily close to , those relatively close work relatively well for linear approximations. The slope
, those relatively close work relatively well for linear approximations. The slope  should be, most accurately, the slope of the tangent line at
should be, most accurately, the slope of the tangent line at  .
.
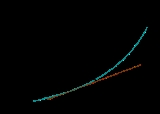
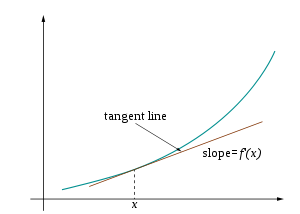 Visually, the accompanying diagram shows the tangent line of
Visually, the accompanying diagram shows the tangent line of 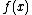 at x. At
at x. At 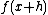 , where
, where 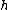 is any small positive or negative value, f(x+h) is very nearly the value of the tangent line at the point
is any small positive or negative value, f(x+h) is very nearly the value of the tangent line at the point 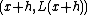 .
.
The final equation for the linearization of a function at is:
is:
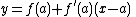
For ,
, 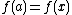 . The derivative
. The derivative
of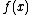 is
is 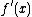 , and the slope of
, and the slope of 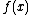 at
at  is
is 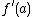 .
.
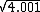 , we can use the fact that
, we can use the fact that  . The linearization of
. The linearization of 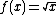 at
at  is
is 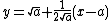 , because the function
, because the function 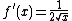 defines the slope of the function
defines the slope of the function 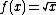 at
at  . Substituting in
. Substituting in 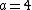 , the linearization at 4 is
, the linearization at 4 is 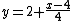 . In this case
. In this case  , so
, so  is approximately
is approximately  . The true value is close to 2.00024998, so the linearization approximation has a relative error of less than 1 millionth of a percent.
. The true value is close to 2.00024998, so the linearization approximation has a relative error of less than 1 millionth of a percent.
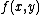 at a point
at a point 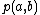 is:
is:

The general equation for the linearization of a multivariable function at a point
at a point 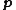 is:
is:
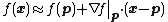
where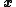 is the vector of variables, and
is the vector of variables, and 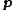 is the linearization point of interest
is the linearization point of interest
.
s to analyze the behavior of a nonlinear function near a given point. The linearization of a function is the first order term of its Taylor expansion around the point of interest. For a system defined by the equation
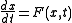 ,
,
the linearized system can be written as
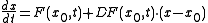
where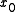 is the point of interest and
is the point of interest and  is the Jacobian
is the Jacobian
of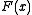 evaluated at
evaluated at 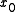 .
.
analysis, one can use the eigenvalues of the Jacobian matrix evaluated at an equilibrium point to determine the nature of that equilibrium. If all of the eigenvalues are positive, the equilibrium is unstable; if they are all negative the equilibrium is stable; and if the values are of mixed signs, the equilibrium is possibly a saddle point
. Any complex
eigenvalues will appear in complex conjugate
pairs and indicate a spiral
.
, decision rules
may be approximated under the state-space approach to linearization. Under this approach, the Euler equations of the utility maximization problem
are linearized around the stationary steady state. A unique solution to the resulting system of dynamic equations then is found.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and its applications, linearization refers to finding the linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
to a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
at a given point. In the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, linearization is a method for assessing the local stability
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
of an equilibrium point of a system
System
System is a set of interacting or interdependent components forming an integrated whole....
of nonlinear differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s or discrete dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. This method is used in fields such as engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
.
Linearization of a function
Linearizations of a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
are lines
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
— ones that are usually used for purposes of calculation. Linearization is an effective method for approximating the output of a function
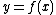 at any
at any  based on the value and slope
based on the value and slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the function at
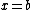 , given that f(x) is continuous on
, given that f(x) is continuous on  (or
(or 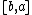 ) and that
) and that  is close to
is close to 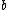 . In, short, linearization approximates the output of a function near
. In, short, linearization approximates the output of a function near  .
.For example, you might know that
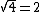 . However, without a calculator, what would be a good approximation of
. However, without a calculator, what would be a good approximation of 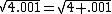 ?
?For any given function
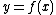 ,
, 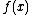 can be approximated if it is near a known continuous point. The most basic requisite is that, where
can be approximated if it is near a known continuous point. The most basic requisite is that, where 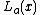 is the linearization of f(x) at x = a,
is the linearization of f(x) at x = a, 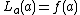 . The point-slope form of an equation forms an equation of a line, given a point
. The point-slope form of an equation forms an equation of a line, given a point 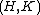 and slope
and slope  . The general form of this equation is:
. The general form of this equation is: 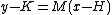 .
.Using the point
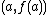 ,
, 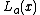 becomes
becomes 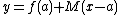 . Because continuous functions are locally linear
. Because continuous functions are locally linearLocal linearity
Local linearity is a property of functions that says — roughly — that the more you zoom in on a point on the graph of the function , the more the graph will look like a straight line. More precisely, a function is locally linear at a point if and only if a tangent line exists at that point...
, the best slope to substitute in would be the slope of the line tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to
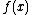 at
at  .
.While the concept of local linearity applies the most to points arbitrarily close to
 , those relatively close work relatively well for linear approximations. The slope
, those relatively close work relatively well for linear approximations. The slope 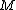 should be, most accurately, the slope of the tangent line at
should be, most accurately, the slope of the tangent line at  .
.
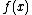 at x. At
at x. At 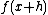 , where
, where 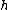 is any small positive or negative value, f(x+h) is very nearly the value of the tangent line at the point
is any small positive or negative value, f(x+h) is very nearly the value of the tangent line at the point 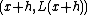 .
.The final equation for the linearization of a function at
 is:
is: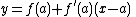
For
 ,
, 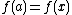 . The derivative
. The derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
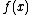 is
is 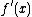 , and the slope of
, and the slope of 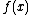 at
at  is
is 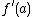 .
.Example
To find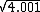 , we can use the fact that
, we can use the fact that  . The linearization of
. The linearization of 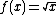 at
at  is
is 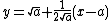 , because the function
, because the function 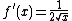 defines the slope of the function
defines the slope of the function 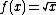 at
at  . Substituting in
. Substituting in 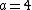 , the linearization at 4 is
, the linearization at 4 is 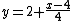 . In this case
. In this case  , so
, so  is approximately
is approximately  . The true value is close to 2.00024998, so the linearization approximation has a relative error of less than 1 millionth of a percent.
. The true value is close to 2.00024998, so the linearization approximation has a relative error of less than 1 millionth of a percent.Linearization of a multivariable function
The equation for the linearization of a function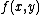 at a point
at a point 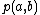 is:
is:
The general equation for the linearization of a multivariable function
 at a point
at a point 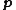 is:
is: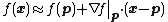
where
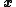 is the vector of variables, and
is the vector of variables, and 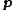 is the linearization point of interest
is the linearization point of interest.
Uses of linearization
Linearization makes it possible to use tools for studying linear systemLinear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s to analyze the behavior of a nonlinear function near a given point. The linearization of a function is the first order term of its Taylor expansion around the point of interest. For a system defined by the equation
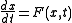 ,
,the linearized system can be written as
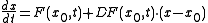
where
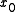 is the point of interest and
is the point of interest and  is the Jacobian
is the JacobianJacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of
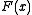 evaluated at
evaluated at 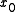 .
.Stability analysis
In stabilityStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
analysis, one can use the eigenvalues of the Jacobian matrix evaluated at an equilibrium point to determine the nature of that equilibrium. If all of the eigenvalues are positive, the equilibrium is unstable; if they are all negative the equilibrium is stable; and if the values are of mixed signs, the equilibrium is possibly a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
. Any complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
eigenvalues will appear in complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
pairs and indicate a spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...
.
Microeconomics
In microeconomicsMicroeconomics
Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
, decision rules
Decision rules
A set of decision rules is the verbal equivalent of a graphical decision tree, which specifies class membership based on a hierarchical sequence of decisions...
may be approximated under the state-space approach to linearization. Under this approach, the Euler equations of the utility maximization problem
Utility maximization problem
In microeconomics, the utility maximization problem is the problem consumers face: "how should I spend my money in order to maximize my utility?" It is a type of optimal decision problem.-Basic setup:...
are linearized around the stationary steady state. A unique solution to the resulting system of dynamic equations then is found.
See also
- Tangent stiffness matrixTangent stiffness matrixIn computational mechanics, a tangent stiffness matrix is a matrix that describes the stiffness of a system in response to small changes in configuration...
- Stability derivativesStability derivativesStability Derivatives, and also Control Derivatives, are measures of how particular forces and moments on an aircraft change as other parameters related to stability change . For a defined "trim" flight condition, changes and oscillations occur in these parameters...
- Linearization theorem
- Taylor approximation

