
Planck constant
Encyclopedia
| Values of h | Units |
|---|---|
| J Joule The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second... ·s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
|
| eV·s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
|
| erg Erg An erg is the unit of energy and mechanical work in the centimetre-gram-second system of units, symbol "erg". Its name is derived from the Greek ergon, meaning "work".... ·s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
|
| Values of ħ | Units |
| J Joule The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second... ·s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
|
| eV·s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
|
| erg Erg An erg is the unit of energy and mechanical work in the centimetre-gram-second system of units, symbol "erg". Its name is derived from the Greek ergon, meaning "work".... ·s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |

The Planck constant (denoted h), also called Planck's constant, is a physical constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
reflecting the sizes of energy quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. It is named after Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
, one of the founders of quantum theory
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, who discovered it in 1899. Classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
requires the existence of h (but does not define its value).
The Planck constant was first described as the proportionality constant between the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
(E) of a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
and the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of its associated electromagnetic wave (ν). This relation between the energy and frequency is called the Planck relation or the Planck–Einstein equation:

Since the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
 , wavelength
, wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ, and speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c are related by , the Planck relation can also be expressed as
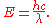
In 1923, Louis de Broglie generalized this relation by postulating that the Planck constant represents the proportionality between the momentum and the quantum wavelength of not just the photon, but any particle. This was confirmed by experiments soon afterwards.
Planck discovered that physical action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
could not take on any indiscriminate value. Instead, the action must be some multiple of a very small quantity (later to be named the "quantum
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
of action" and now called Planck's constant). This inherent granularity is counterintuitive in the everyday world, where it is possible to "make things a little bit hotter" or "move things a little bit faster". This is because the quanta of action are very, very small in comparison to everyday human experience. Thus, on the macro scale quantum mechanics and classical physics converge. Nevertheless, it is impossible, as Planck found out, to explain some phenomena without accepting that action is quantized. In many cases, such as for monochromatic light or for atoms, the quantum of action also implies that only certain energy levels are allowed, and values in between are forbidden.
In applications where frequency is expressed in terms of radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s per second ("angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
") instead of cycles per second
Cycle per second
The cycle per second was a once-common unit of frequency.With the organization of the International System of Units in 1960, the cycle per second was officially replaced by the hertz, or reciprocal second—i.e. the cycle in 'cycle per second' was dropped...
, it is often useful to absorb a factor of 2π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
into the Planck constant. The resulting constant is called the reduced Planck constant or Dirac constant. It is equal to the Planck constant divided by 2π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, and is denoted ħ ("h-bar"):
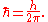
The energy of a photon with angular frequency ω, where ω = 2πν, is given by

Value
The Planck constant has dimensionDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
s of physical action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
; these are the same as those of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, i.e., energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
multiplied by time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, or momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
multiplied by distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
. In SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
, the Planck constant is expressed in joule seconds or .
The value of the Planck constant is:
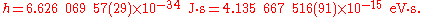
The value of the reduced Planck constant is:

The two digits between the parentheses denote the standard uncertainty
Measurement uncertainty
In metrology, measurement uncertainty is a non-negative parameter characterizing the dispersion of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured...
in the last two digits of the value. The figures cited here are the 2010 CODATA recommended values for the constants and their uncertainties. The 2010 CODATA results were made available in June 2011 and represent the best-known, internationally-accepted values for these constants, based on all data available as of 2010. New CODATA figures are scheduled to be published approximately every four years.
Significance of the value
The numerical value of the Planck constant depends entirely on the system of units used to measure it. When it is expressed in SI units, it is one of the smallest constants used in physics. This reflects the fact that, on a scale adapted to humans, where energies are typically of the order of kilojoules and times are typically of the order of seconds or minutes, Planck's constant, the quantum of action, is very small.Equivalently, the smallness of Planck's constant reflects the fact that everyday objects and systems are made of large number of particles. To take one example, green light of a wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of 555 nanometre
Nanometre
A nanometre is a unit of length in the metric system, equal to one billionth of a metre. The name combines the SI prefix nano- with the parent unit name metre .The nanometre is often used to express dimensions on the atomic scale: the diameter...
s (approximately the wavelength to which human eyes are most sensitive) has a frequency of 540 THz (540 Hz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
). Each photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
has an energy E of hν = 3.58 J. That is a very small energy in terms of everyday experience, but then everyday experience doesn't deal with individual photons any more than it deals with individual atoms or molecules. An amount of light that is compatible with everyday experience
is the energy of one mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
of photons; its energy can be calculated by multiplying the photon energy by the Avogadro constant, NA ≈ . The result is that green light of wavelength 555 nm has an energy of 216 kJ/mol, a typical energy of everyday life.
The Planck constant is related to the quantization of light and matter. Therefore, the Planck constant can be seen as an atomic-scale constant. In a unit system adapted to atomic scales, the electronvolt
Electronvolt
In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
is the appropriate unit of energy and the Petahertz the appropriate unit of frequency. In such an atomic units
Atomic units
Atomic units form a system of natural units which is especially convenient for atomic physics calculations. There are two different kinds of atomic units, which one might name Hartree atomic units and Rydberg atomic units, which differ in the choice of the unit of mass and charge. This article...
system, Planck's constant is indeed described by a number of order 1.
Black-body radiation
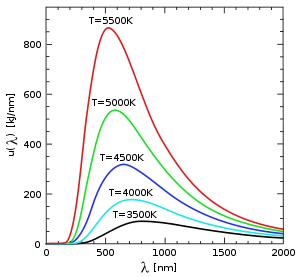
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
first posed by Kirchhoff
Gustav Kirchhoff
Gustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
some forty years earlier. It is well known that hot objects glow, and that hotter objects glow brighter than cooler ones. The reason is that the electromagnetic field obeys laws of motion just like a mass on a spring, and can come to thermal equilibrium with hot atoms. When a hot object is in equilibrium with light, the amount of light it absorbs is equal to the amount of light it emits. If the object is black, meaning it absorbs all the light that hits it, then it emits the maximum amount of thermal light too.
The assumption that blackbody radiation is thermal leads to an accurate prediction: the total amount of emitted energy goes up with the temperature according to a definite rule, the Stefan–Boltzmann law (1879–84). But it was also known that the colour of the light given off by a hot object changes with the temperature, so that "white hot" is hotter than "red hot". Nevertheless, Wilhelm Wien
Wilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien was a German physicist who, in 1893, used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any temperature from the emission at any one reference temperature.He also formulated an...
discovered the mathematical relationship between the peaks of the curves at different temperatures, by using the principle of adiabatic invariance
Adiabatic invariant
An adiabatic invariant is a property of a physical system that stays constant when changes occur slowly.In thermodynamics, an adiabatic process is a change that occurs without heat flow, and slowly compared to the time to reach equilibrium. In an adiabatic process, the system is in equilibrium at...
. At each different temperature, the curve is moved over by Wien's displacement law
Wien's displacement law
Wien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph...
(1893). Wien also proposed an approximation for the spectrum of the object, which was correct at high frequencies (short wavelength) but not at low frequencies (long wavelength). It still was not clear why the spectrum of a hot object had the form that it has (see diagram).
Planck hypothesized that the equations of motion for light are a set of harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s, one for each possible frequency. He examined how the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for black-body spectrum.
However, Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators. To save his theory, Planck had to resort to using the then controversial theory of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, which he described as "an act of despair … I was ready to sacrifice any of my previous convictions about physics." One of his new boundary conditions was
With this new condition, Planck had imposed the quantization of the energy of the oscillators, "a purely formal assumption … actually I did not think much about it…" in his own words, but one which would revolutionize physics. Applying this new approach to Wien's displacement law showed that the "energy element" must be proportional to the frequency of the oscillator, the first version of what is now termed "Planck's relation":

Planck was able to calculate the value of h from experimental data on black-body radiation: his result, , is within 1.2% of the currently accepted value. He was also able to make the first determination of the Boltzmann constant kB from the same data and theory.
Prior to Planck's work, it had been assumed that the energy of a body could take on any value whatsoever – that it was a continuous variable
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. The Rayleigh-Jeans law
Rayleigh-Jeans law
In physics, the Rayleigh–Jeans law attempts to describe the spectral radiance of electromagnetic radiation at all wavelengths from a black body at a given temperature through classical arguments. For wavelength λ, it is;...
makes close predictions for a narrow range of values at one limit of temperatures, but the results diverge more and more strongly as temperatures increase. To make Planck's law, which correctly predicts blackbody emissions, it was necessary to multiply the classical expression by a complex factor that involves h in both the numerator and the denominator. The influence of h in this complex factor would not disappear if it were set to zero or to any other value. Making an equation out of Planck's law that would reproduce the Rayleigh-Jeans law could not be done by changing the values of h, of the Boltzmann constant, or of any other constant or variable in the equation. In this case the picture given by classical physics is not duplicated by a range of results in the quantum picture.
The black-body problem was revisited in 1905, when Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
and Jeans
James Hopwood Jeans
Sir James Hopwood Jeans OM FRS MA DSc ScD LLD was an English physicist, astronomer and mathematician.-Background:...
(on the one hand) and Einstein (on the other hand) independently proved that classical electromagnetism could never account for the observed spectrum. These proofs are commonly known as the "ultraviolet catastrophe
Ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
", a name coined by Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
in 1911. They contributed greatly (along with Einstein's work on the photoelectric effect) to convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The very first Solvay Conference
Solvay Conference
The International Solvay Institutes for Physics and Chemistry, located in Brussels, were founded by the Belgian industrialist Ernest Solvay in 1912, following the historic invitation-only 1911 Conseil Solvay, the turning point in world physics...
in 1911 was devoted to "the theory of radiation and quanta". Max Planck received the 1918 Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
"in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta".
Photoelectric effect
The photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shone on it. It was first observed by Alexandre Edmond Becquerel in 1839, although credit is usually reserved for Heinrich Hertz, who published the first thorough investigation in 1887. Another particularly thorough investigation was published by Philipp LenardPhilipp Lenard
Philipp Eduard Anton von Lenard , known in Hungarian as Lénárd Fülöp Eduárd Antal, was a Hungarian - German physicist and the winner of the Nobel Prize for Physics in 1905 for his research on cathode rays and the discovery of many of their properties...
in 1902. Einstein's 1905 paper discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921, when his predictions had been confirmed by the experimental work of Robert Andrews Millikan. To put it another way, in 1921 at least, Einstein's theories on the photoelectric effect were considered more important than his theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
(a name coined, as it happens, by Max Planck).
Prior to Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterise different types of radiation. The energy transferred by a wave in a given time is called its intensity
Intensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
. The light from a theatre spotlight is more intense than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time (and hence consumes more electricity) than the ordinary bulb, even though the colour of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their own intensity. However the energy account of the photoelectric effect didn't seem to agree with the wave description of light.
The "photoelectrons" emitted as a result of the photoelectric effect have a certain kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
, which can be measured. This kinetic energy (for each photoelectron) is independent of the intensity of the light, but depends linearly on the frequency; and if the frequency is too low (corresponding to a kinetic energy for the photoelectrons of zero or less), no photoelectrons are emitted at all, unless a plurality of photons, whose energetic sum is greater than the energy of the photoelectrons, acts virtually simultaneously (multiphoton effect) Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.
Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, was to be the same as Planck's "energy element", giving the modern version of Planck's relation:
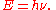
Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light (ν) and the kinetic energy of photoelectrons (E) was shown to be equal to the Planck constant (h).
Atomic structure
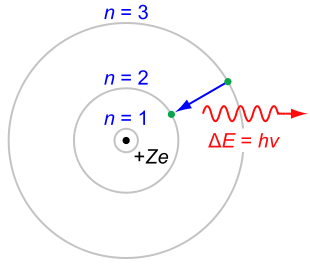
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
introduced the first quantized model of the atom in 1913, in an attempt to overcome a major shortcoming of Rutherford's
Ernest Rutherford
Ernest Rutherford, 1st Baron Rutherford of Nelson OM, FRS was a New Zealand-born British chemist and physicist who became known as the father of nuclear physics...
classical model. In classical electrodynamics, a charge moving in a circle should radiate electromagnetic radiation. If that charge were to be an electron orbiting a nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
, the radiation would cause it to lose energy and spiral down into the nucleus. Bohr solved this paradox with explicit reference to Planck's work: an electron in a Bohr atom could only have certain defined energies En

where R∞ is an experimentally-determined constant (the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
) and n is any integer (n = 1, 2, 3, …). Once the electron reached the lowest energy level , it could not get any closer to the nucleus (lower energy). This approach also allowed Bohr to account for the Rydberg formula
Rydberg formula
The Rydberg formula is used in atomic physics to describe the wavelengths of spectral lines of many chemical elements. It was formulated by the Swedish physicist Johannes Rydberg, and presented on November 5, 1888.-History:...
, an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant R∞ in terms of other fundamental constants.
Bohr also introduced the quantity h/2π, now known as the reduced Planck constant, as the quantum of angular momentum. At first, Bohr thought that this was the angular momentum of each electron in an atom: this proved incorrect and, despite developments by Sommerfeld and others, an accurate description of the electron angular momentum proved beyond the Bohr model. The correct quantization rules for electrons – in which the energy reduces to the Bohr-model equation in the case of the hydrogen atom – were given by Heisenberg's matrix mechanics
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
in 1925 and the Schrödinger wave equation in 1926: the reduced Planck constant remains the fundamental quantum of angular momentum. In modern terms, if J is the total angular momentum of a system with rotational invariance, and Jz the angular momentum measured along any given direction, these quantities can only take on the values
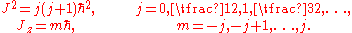
Uncertainty principle
The Planck constant also occurs in statements of Werner HeisenbergWerner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
's uncertainty principle. Given a large number of particles prepared in the same state, the uncertainty
Uncertainty
Uncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
in their position, Δx, and the uncertainty in their momentum (in the same direction), Δp, obey
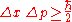
where the uncertainty is given as the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the measured value from its expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. There are a number of other such pairs of physically measurable values which obey a similar rule. One example is time vs. frequency. The either-or nature of uncertainty forces measurement attempts to choose between trade offs, and given that they are quanta, the trade offs often take the form of either-or (as in Fourier analysis), rather than the compromises and gray areas of time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
analysis. A practical example is computational neurology trying to both measure the time effect and frequency of a neuron burst. fMRI (functional MRI), whose signal processing is based on Fourier transforms, can resolve frequency, but not time (a limit of Fourier analysis due to uncertainty). An EEG
EEG
EEG commonly refers to electroencephalography, a measurement of the electrical activity of the brain.EEG may also refer to:* Emperor Entertainment Group, a Hong Kong-based entertainment company...
(a time series analysis measurement tool) can resolve time, but not frequency. Due to uncertainty, these are not problems with the design of the measuring instruments, but problems with the nature of quantum measurement and particle realities themselves.
In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
relationship between the position operator
 and the momentum operator
and the momentum operator 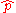 :
:
where δij is the Kronecker delta.
Dependent physical constants
The following list is based on the 2006 CODATA evaluation; for the constants listed below, more than 90% of the uncertainty is due to the uncertainty in the value of the Planck constant, as indicated by the square of the correlation coefficientPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
(r2 > 0.9, r > 0.949). The Planck constant is (with one or two exceptions) the fundamental physical constant which is known to the lowest level of precision, with a relative uncertainty
Measurement uncertainty
In metrology, measurement uncertainty is a non-negative parameter characterizing the dispersion of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured...
ur of 5.0.
Rest mass of the electron
The normal textbook derivation of the Rydberg constantRydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
R∞ defines it in terms of the electron mass me and a variety of other physical constants.
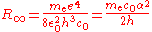
However, the Rydberg constant can be determined very accurately (ur = 6.6) from the atomic spectrum of hydrogen, whereas there is no direct method to measure the mass of a stationary electron in SI units. Hence the equation for the calculation of me becomes

where c0 is the speed of light and α is the fine-structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
. The speed of light has an exactly defined value in SI units, and the fine-structure constant can be determined more accurately (ur = 6.8) than the Planck constant: the uncertainty in the value of the electron rest mass is due entirely to the uncertainty in the value of the Planck constant (r2 > 0.999).
Avogadro constant
The Avogadro constant NA is determined as the ratio of the mass of one mole of electrons to the mass of a single electron: The mass of one mole of electrons is the "relative atomic mass" of an electron Ar(e), which can be measured in a Penning trapPenning trap
Penning traps are devices for the storage of charged particles using a homogeneous static magnetic field and a spatially inhomogeneous static electric field. This kind of trap is particularly well suited to precision measurements of properties of ions and stable subatomic particles which have...
(ur = 4.2), multiplied by the molar mass constant
Molar mass constant
The molar mass constant, symbol Mu, is a physical constant which relates atomic weight and molar mass. Its value is defined to be 1 g/mol in SI units....
Mu, which is defined as 0.001 kg/mol.
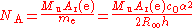
The dependence of the Avogadro constant on the Planck constant (r2 > 0.999) also holds for the physical constants which are related to amount of substance, such as the atomic mass constant
Atomic mass constant
In physics and chemistry, the atomic mass constant, mu, is one twelfth of the mass of an unbound atom of carbon-12 at rest and in its ground state. It serves to define the atomic mass unit and is, by definition, equal to 1 u...
. The uncertainty in the value of the Planck constant limits the knowledge of the masses of atoms and subatomic particles when expressed in SI units. It is possible to measure the masses more precisely in atomic mass unit
Atomic mass unit
The unified atomic mass unit or dalton is a unit that is used for indicating mass on an atomic or molecular scale. It is defined as one twelfth of the rest mass of an unbound neutral atom of carbon-12 in its nuclear and electronic ground state, and has a value of...
s, but not to convert them more precisely into kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
s.
Elementary charge
SommerfeldArnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
originally defined the fine-structure constant α as:
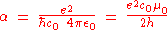
where e is the elementary charge
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
, ε0 is the electric constant
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
(also called the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of free space), and μ0 is the magnetic constant (also called the permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
of free space). The latter two constants have fixed values in the International System of Units
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
. However, α can also be determined experimentally, notably by measuring the electron spin g-factor ge, then comparing the result with the value predicted by quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
.
At present, the most precise value for the elementary charge is obtained by rearranging the definition of α to obtain the following definition of e in terms of α and h:

Bohr magneton and nuclear magneton
The Bohr magneton and the nuclear magneton are units which are used to describe the magnetic properties of the electron and atomic nuclei respectively. The Bohr magneton is the magnetic momentMagnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
which would be expected for an electron if it behaved as a spinning charge according to classical electrodynamics. It is defined in terms of the reduced Planck constant, the elementary charge and the electron mass, all of which depend on the Planck constant: the final dependence on h½ (r2 > 0.995) can be found by expanding the variables.
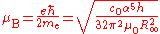
The nuclear magneton has a similar definition, but corrected for the fact that the proton is much more massive than the electron. The ratio of the electron relative atomic mass to the proton relative atomic mass can be determined experimentally to a high level of precision (ur = 4.3).
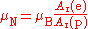
Determination
| Method | Value of h (10−34 J·s) |
Relative uncertainty |
Ref. |
|---|---|---|---|
| Watt balance | 3.4 | ||
| X-ray crystal density | 2.9 | ||
| Josephson constant | 4.1 | ||
| Magnetic resonance | 8.6 | ||
| Faraday constant | 1.3 | ||
| CODATA 2010 recommended value |
4.4 | ||
| The nine recent determinations of the Planck constant cover five separate methods. Where there is more than one recent determination for a given method, the value of h given here is a weighted mean of the results, as calculated by CODATA. | |||
In principle, the Planck constant could be determined by examining the spectrum of a black-body radiator or the kinetic energy of photoelectrons, and this is how its value was first calculated in the early twentieth century. In practice, these are no longer the most accurate methods. The CODATA value quoted here is based on three watt-balance measurements of KJ2RK and one inter-laboratory determination of the molar volume of silicon, but is mostly determined by a 2007 watt-balance measurement made at the U.S. National Institute of Standards and Technology
National Institute of Standards and Technology
The National Institute of Standards and Technology , known between 1901 and 1988 as the National Bureau of Standards , is a measurement standards laboratory, otherwise known as a National Metrological Institute , which is a non-regulatory agency of the United States Department of Commerce...
(NIST). Five other measurements by three different methods were initially considered, but not included in the final refinement as they were too imprecise to affect the result.
There are both practical and theoretical difficulties in determining h. The practical difficulties can be illustrated by the fact that the two most accurate methods, the watt balance
Watt balance
The watt balance is an experimental electromechanical weight measuring instrument that measures the weight of a test object very precisely by the strength of an electric current and a voltage. It is being developed as a metrological instrument that may one day provide a definition of the kilogram...
and the X-ray crystal density method, do not appear to agree with one another. The most likely reason is that the measurement uncertainty for one (or both) of the methods has been estimated too low – it is (or they are) not as precise as is currently believed – but for the time being there is no indication which method is at fault.
The theoretical difficulties arise from the fact that all of the methods except the X-ray crystal density method rely on the theoretical basis of the Josephson effect
Josephson effect
The Josephson effect is the phenomenon of supercurrent across two superconductors coupled by a weak link...
and the quantum Hall effect. If these theories are slightly inaccurate – though there is no evidence at present to suggest they are – the methods would not give accurate values for the Planck constant. More importantly, the values of the Planck constant obtained in this way cannot be used as tests of the theories without falling into a circular argument. Fortunately, there are other statistical ways of testing the theories, and the theories have yet to be refuted.
Josephson constant
The Josephson constant KJ relates the potential difference U generated by the Josephson effectJosephson effect
The Josephson effect is the phenomenon of supercurrent across two superconductors coupled by a weak link...
at a "Josephson junction" with the frequency ν of the microwave radiation. The theoretical treatment of Josephson effect suggests very strongly that KJ = 2e/h.
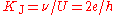
The Josephson constant may be measured by comparing the potential difference generated by an array of Josephson junctions with a potential difference which is known in SI volt
Volt
The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
s. The measurement of the potential difference in SI units is done by allowing an electrostatic force to cancel out a measurable gravitational force. Assuming the validity of the theoretical treatment of the Josephson effect, KJ is related to the Planck constant by
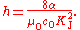
Watt balance
A watt balance is an instrument for comparing two powersPower (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
, one of which is measured in SI watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s and the other of which is measured in conventional electrical unit
Conventional electrical unit
A conventional electrical unit is a unit of measurement in the field of electricity which is based on the conventional values of the Josephson constant and the von Klitzing constant agreed by the International Committee for Weights and Measures in 1988...
s. From the definition of the conventional watt W90, this gives a measure of the product KJ2RK in SI units, where RK is the von Klitzing constant which appears in the quantum Hall effect. If the theoretical treatments of the Josephson effect and the quantum Hall effect are valid, and in particular assuming that RK = h/e2, the measurement of KJ2RK is a direct determination of the Planck constant.
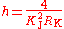
Magnetic resonance
The gyromagnetic ratio γ is the constant of proportionality between the frequency ν of nuclear magnetic resonanceNuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
(or electron paramagnetic resonance
Electron paramagnetic resonance
Electron paramagnetic resonance or electron spin resonance spectroscopyis a technique for studying chemical species that have one or more unpaired electrons, such as organic and inorganic free radicals or inorganic complexes possessing a transition metal ion...
for electrons) and the applied magnetic field B: ν = γB. It is difficult to measure gyromagnetic ratios precisely because of the difficulties in precisely measuring B, but the value for proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s in water at 25 °C is known to better than one part per million. The protons are said to be "shielded" from the applied magnetic field by the electrons in the water molecule, the same effect that gives rise to chemical shift
Chemical shift
In nuclear magnetic resonance spectroscopy, the chemical shift is the resonant frequency of a nucleus relative to a standard. Often the position and number of chemical shifts are diagnostic of the structure of a molecule...
in NMR spectroscopy, and this is indicated by a prime on the symbol for the gyromagnetic ratio, γ′p. The gyromagnetic ratio is related to the shielded proton magnetic moment μ′p, the spin number I (I = for protons) and the reduced Planck constant.
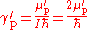
The ratio of the shielded proton magnetic moment μ′p to the electron magnetic moment μe can be measured separately and to high precision, as the imprecisely-known value of the applied magnetic field cancels itself out in taking the ratio. The value of μe in Bohr magnetons is also known: it is half the electron g-factor ge. Hence
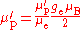
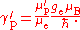
A further complication is that the measurement of γ′p involves the measurement of an electric current: this is invariably measured in conventional amperes rather than in SI ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
s, so a conversion factor is required. The symbol Γ′p-90 is used for the measured gyromagnetic ratio using conventional electrical units. In addition, there are two methods of measuring the value, a "low-field" method and a "high-field" method, and the conversion factors are different in the two cases. Only the high-field value Γ′p-90(hi) is of interest in determining the Planck constant.

Substitution gives the expression for the Planck constant in terms of Γ′p-90(hi):
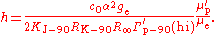
Faraday constant
The Faraday constant F is the chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of one mole of electrons, equal to the Avogadro constant NA multiplied by the elementary charge e. It can be determined by careful electrolysis
Electrolysis
In chemistry and manufacturing, electrolysis is a method of using a direct electric current to drive an otherwise non-spontaneous chemical reaction...
experiments, measuring the amount of silver
Silver
Silver is a metallic chemical element with the chemical symbol Ag and atomic number 47. A soft, white, lustrous transition metal, it has the highest electrical conductivity of any element and the highest thermal conductivity of any metal...
dissolved from an electrode in a given time and for a given electric current. In practice, it is measured in conventional electrical units, and so given the symbol F90. Substituting the definitions of NA and e, and converting from conventional electrical units to SI units, gives the relation to the Planck constant.

X-ray crystal density
The X-ray crystal density method is primarily a method for determining the Avogadro constant NA but as the Avogadro constant is related to the Planck constant it also determines a value for h. The principle behind the method is to determine NA as the ratio between the volume of the unit cell of a crystal, measured by X-ray crystallographyX-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
, and the molar volume
Molar volume
The molar volume, symbol Vm, is the volume occupied by one mole of a substance at a given temperature and pressure. It is equal to the molar mass divided by the mass density...
of the substance. Crystals of silicon
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
are used, as they are available in high quality and purity by the technology developed for the semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
industry. The unit cell volume is calculated from the spacing between two crystal planes referred to as d220. The molar volume Vm(Si) requires a knowledge of the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the crystal and the atomic weight
Atomic weight
Atomic weight is a dimensionless physical quantity, the ratio of the average mass of atoms of an element to 1/12 of the mass of an atom of carbon-12...
of the silicon used. The Planck constant is given by
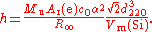
Fixation
As mentioned above, the numerical value of the Planck constant depends on the system of units used to describe it. Its value in SI units is known to 50 parts per billion but its value in atomic units is known exactly, because of the way the scale of atomic units is defined. The same is true of conventional electrical units, where the Planck constant (noted h90 to distinguish it from its value in SI units) is given by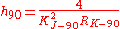
with KJ–90 and RK–90 being exactly defined constants. Atomic units and conventional electrical units are very useful in their respective fields, because the uncertainty in the final result doesn't depend on an uncertain conversion factor, only on the uncertainty of the measurement itself.
There are a number of proposals to redefine certain of the SI base unit
SI base unit
The International System of Units defines seven units of measure as a basic set from which all other SI units are derived. These SI base units and their physical quantities are:* metre for length...
s in terms of fundamental physical constants. This has already been done for the metre, which is defined in terms of a fixed value of the speed of light. The most urgent unit on the list for redefinition is the kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
, whose value has been fixed for all science (since 1889) by the mass of a small cylinder of platinum
Platinum
Platinum is a chemical element with the chemical symbol Pt and an atomic number of 78. Its name is derived from the Spanish term platina del Pinto, which is literally translated into "little silver of the Pinto River." It is a dense, malleable, ductile, precious, gray-white transition metal...
–iridium
Iridium
Iridium is the chemical element with atomic number 77, and is represented by the symbol Ir. A very hard, brittle, silvery-white transition metal of the platinum family, iridium is the second-densest element and is the most corrosion-resistant metal, even at temperatures as high as 2000 °C...
alloy kept in vault just outside Paris. While nobody knows if the mass of the International Prototype Kilogram has "changed" since 1889 – the value 1 kg of its mass expressed in kilograms is by definition unchanged and therein lies one of the problems – it is known that over such a timescale the many similar Pt–Ir alloy cylinders kept in national laboratories around the world, have changed their relative mass by several tens of parts per million, however carefully they are stored, and the more so, the more they have been taken out and used as mass standards. A change of several tens of micrograms in one kilogram is equivalent to the current uncertainty in the value of the Planck constant in SI units.
The legal process to change the definition of the kilogram is already underway, but it was decided that no final decision would be made before the next meeting of the General Conference on Weights and Measures
General Conference on Weights and Measures
The General Conference on Weights and Measures is the English name of the Conférence générale des poids et mesures . It is one of the three organizations established to maintain the International System of Units under the terms of the Convention du Mètre of 1875...
in 2011. The Planck constant is a leading contender to form the basis of the new definition, although not the only one. Possible new definitions include "the mass of a body at rest whose equivalent energy equals the energy of photons whose frequencies sum to ", or simply "the kilogram is defined so that the Planck constant equals ".
The BIPM provided Draft Resolution A in anticipation of the 24th General Conference on Weights and Measures meeting (2011-10-17 though 2011-10-21), detailing the considerations "On the possible future revision of the International System of Units, the SI".
Watt balances already measure mass in terms of the Planck constant: at present, standard mass is taken as "fixed" and the measurement is performed to determine the Planck constant but, were the Planck constant to be fixed in SI units, the same experiment would be a measurement of the mass. The relative uncertainty in the measurement would remain the same.
Mass standards could also be constructed from silicon crystals or by other "atom-counting" methods. Such methods require a knowledge of the Avogadro constant, which fixes the proportionality between atomic mass
Atomic mass
The atomic mass is the mass of a specific isotope, most often expressed in unified atomic mass units. The atomic mass is the total mass of protons, neutrons and electrons in a single atom....
and macroscopic mass but, with a defined value of the Planck constant, NA would be known to the same level of uncertainty (if not better) than current methods of comparing macroscopic mass.
Computing codes
The symbol for the Planck constant is , similar to an italic lowercase letter HH
H .) is the eighth letter in the basic modern Latin alphabet.-History:The Semitic letter ⟨ח⟩ most likely represented the voiceless pharyngeal fricative . The form of the letter probably stood for a fence or posts....
(h); the symbol for the reduced Planck constant is , similar to an italic lowercase letter H with stroke (ħ).
| character | ||||
| Unicode name | PLANCK CONSTANT | PLANCK CONSTANT OVER TWO PI | ||
| character encoding | decimal | hex | decimal | hex |
| Unicode Unicode Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems... |
8462 | 210E | 8463 | 210F |
| UTF-8 UTF-8 UTF-8 is a multibyte character encoding for Unicode. Like UTF-16 and UTF-32, UTF-8 can represent every character in the Unicode character set. Unlike them, it is backward-compatible with ASCII and avoids the complications of endianness and byte order marks... |
226 132 142 | E2 84 8E | 226 132 143 | E2 84 8F |
| Numeric character reference Numeric character reference A numeric character reference is a common markup construct used in SGML and other SGML-related markup languages such as HTML and XML. It consists of a short sequence of characters that, in turn, represent a single character from the Universal Character Set of Unicode... |
ℎ | ℎ | ℏ | ℏ |
See also
- Basic concepts of quantum mechanicsBasic concepts of quantum mechanicsQuantum mechanics explains the behaviour of matter and energy on the scale of atoms and subatomic particles.Classical physics explains matter and energy at the macroscopic level of the scale familiar to human experience, including the behavior of astronomical bodies...
- Planck unitsPlanck unitsIn physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
- Wave–particle dualityWave–particle dualityWave–particle duality postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale objects...
- Stigler's law

