Adiabatic invariant
Encyclopedia
An adiabatic invariant is a property of a physical system
that stays constant when changes occur slowly.
In thermodynamics
, an adiabatic process is a change that occurs without heat flow, and slowly compared to the time to reach equilibrium. In an adiabatic process, the system is in equilibrium at all stages. Under these conditions, the entropy
is constant.
In mechanics
, an adiabatic change is a slow deformation of the Hamiltonian
, where the fractional rate of change
of the energy is much slower than the orbital frequency. The area enclosed by the different motions in phase space are the adiabatic invariants.
In quantum mechanics
, an adiabatic change is one that occurs at a rate much slower than the difference in frequency between energy eigenstates. In this case, the energy states of the system do not make transitions, so that the quantum number
is an adiabatic invariant.
The old quantum theory
was formulated by equating the quantum number of a system with its classical adiabatic invariant. This determined the form of the Bohr-Sommerfeld quantization rule: the quantum number is the area in phase space of the classical orbit.
is expanded instantaneously, the temperature of the gas doesn't change at all, because none of the molecules slow down. The molecules keep their kinetic energy, but now the gas occupies a bigger volume. If the container expands slowly, however, so that the ideal gas pressure law holds at any time, gas molecules lose energy at the rate that they do work on the expanding wall. The amount of work they do is the pressure times the area of the wall times the outward displacement, which is the pressure times the change in the volume of the gas: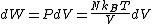
If no heat enters the gas, the energy in the gas molecules is decreasing by the same amount. By definition, a gas is ideal when its temperature is only a function of the internal energy per particle, not the volume. So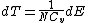
Where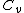
is the specific heat at constant volume. When the change in energy is entirely due to work done on the wall, the change in temperature is given by: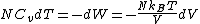
This gives a differential relationship between the changes in temperature and volume, which can be integrated to find the invariant. The constant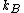
is just a unit conversion factor
, which can be set equal to one: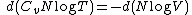
So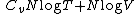
is an adiabatic invariant, which is related to the entropy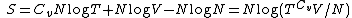
So entropy is an adiabatic invariant. The N log(N) term makes the entropy additive, so the entropy of two volumes of gas is the sum of the entropies of each one.
In a molecular interpretation, S is the logarithm of the phase space volume of all gas states with energy E(T) and volume V.
For a monatomic ideal gas, this can easily be seen by writing down the energy,
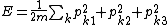
The different internal motions of the gas with total energy E define a sphere, the surface of a 3N-dimensional ball with radius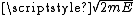
. The volume of the sphere is
,
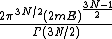where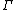
is the Gamma function
.
Since each gas molecule can be anywhere within the volume V, the volume in phase space occupied by the gas states with energy E is
.
Since the N gas molecules are indistinguishable, the phase space volume is divided by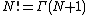
, the number of permutations of N molecules.
Using Stirling's approximation
for the gamma function, and ignoring factors that disappear in the logarithm after taking N large,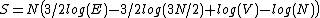
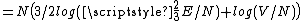
Since the specific heat of a monatomic gas is 3/2, this is the same as the thermodynamic formula for the entropy.
, since equipartition demands that each field mode has an equal energy on average and there are infinitely many modes. This is physically ridiculous, since it means that all energy leaks into high frequency electromagnetic waves over time.
Still, without quantum mechanics, there are some things that can be said about the equilibrium distribution from thermodynamics alone, because there is still a notion of adiabatic invariance that relates boxes of different size.
When a box is slowly expanded, the frequency of the light recoiling from the
wall can be computed from the Doppler shift. If the wall is not moving,
the light recoils at the same frequency. If the wall is moving slowly, the recoil frequency is only equal in the frame where the wall is stationary. In the frame where the wall is moving away from the light, the light coming in is bluer than the light coming out by twice the Doppler shift factor v/c.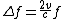
On the other hand, the energy in the light is also decreased when the wall is moving away, because the light is doing work on the wall by radiation pressure. Because the light is reflected, the pressure is equal to twice the momentum carried by light, which is E/c. The rate at which the pressure does work on the wall is found by multiplying by the velocity: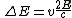
This means that the change in frequency of the light is equal to the work done on the wall by the radiation pressure. The light that is reflected is changed both in frequency and in energy by the same amount: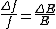
Since moving the wall slowly should keep a thermal distribution fixed, the probability that the light has energy E at frequency f must only be a function of E/f.
This function cannot be determined from thermodynamic reasoning alone, and Wien guessed at the form that was valid at high frequency. He supposed that the average energy in high frequency modes was suppressed by a Boltzmann-like factor. This is not the expected classical energy in the mode, which is
by equipartition, but a new and unjustified assumption that fit the high-frequency data.
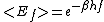
When the expectation value is added over all modes in a cavity, this is Wien's distribution, and it describes the thermodynamic distribution of energy in a classical gas of photons. Wien's Law implicitly assumes that light is statistically composed of packets that change energy and frequency in the same way. The entropy of a Wein gas scales as the volume to the power N, where N is the number of packets. This led Einstein to suggest that light is composed of localizable particles with energy proportional to the frequency. Then the entropy of the Wien gas can be given a statistical interpretation as the number of possible positions that the photons can be in.
The action J of a classical orbit is the area
enclosed by the orbit in phase space.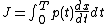
Since J is an integral over a full period, it is only a function of the energy. When
the Hamiltonian is constant in time and J is constant in time, the canonically conjugate variable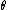
increases in time at a steady rate.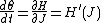
So the constant H' can be used to change time derivatives along the orbit to partial derivatives with respect to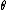
at constant J. Differentiating the integral for J with respect to J gives an identity that fixes H':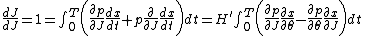
The integrand is the Poisson bracket
of x and p. The Poisson bracket of two canonically conjugate quantities like x and p is equal to 1 in any canonical coordinate system. So
and H' is the inverse period. The variable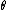
increases by an equal amount in each period for all values of J— it is an angle-variable.
Adiabatic Invariance of J
The Hamiltonian is a function of J only, and in the simple case of the Harmonic oscillator.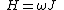
When H has no time dependence, J is constant. When H is slowly time varying, the
rate of change of J can be computed by reexpressing the integral for J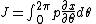
The time derivative of this quantity is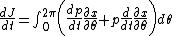
Replacing time derivatives with theta derivatives,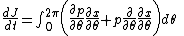
So as long as the coordinates J,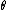
do not change appreciably over one period, this expression can be integrated by parts to give zero. This means
that for slow variations, there is no lowest order change in the area enclosed by
the orbit. This is the adiabatic invariance theorem— the action variables are adiabatic invariants.
For a harmonic oscillator, the area in phase space of an orbit at energy E is the area
of the ellipse of constant energy,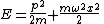
The x-radius of this ellipse is
, while the p-radius of the ellipse is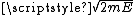 
. Multiplying, the area is 
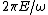. So if a pendulum is slowly drawn in, so that the frequency changes, the energy changes by a proportional amount.
The Planck radiation law quantized the motion of the field oscillators in units of energy proportional to the frequency: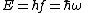
This is the only sensible quantization. The quantum can only depend on the energy/frequency by adiabatic invariance, and since the energy must be additive when putting boxes end to end, the levels must be equally spaced.
Einstein, followed by Debye, extended the domain of quantum mechanics by considering the sound modes in a solid as quantized oscillators
. This model explained why the specific heat of solids approached zero at low temperatures,
instead of staying fixed at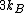
as predicted by classical equipartition
.
At the Solvay conference
, the question of quantizing other motions was raised, and Lorentz
pointed out a problem. If you consider a quantum pendulum whose string is shortened very slowly, the quantum number of the pendulum cannot change because at no point is there a high enough frequency to cause a transition between the states. But the frequency of the pendulum changes when the string is shorter, so the quantum states change energy.
Einstein responded that for slow pulling, the frequency and energy of the pendulum both change but the ratio stays fixed. This is analogous to Wien's observation that under slow motion of the wall the energy to frequency ratio of reflected waves is constant. The conclusion was that the quantities to quantize must be adiabatic invariants.
This line of argument was extended by Sommerfeld into a general theory: the quantum number of an arbitrary mechanical system is given by the adiabatic action variable. Since the action variable in the harmonic oscillator is an integer, the general condition is: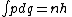
This condition was the foundation of the old quantum theory
, which was able to predict the qualitative behavior of atomic systems. The theory is inexact for small quantum numbers, since it mixes classical and quantum concepts. But it was a useful half-way step to the new quantum theory
.
,
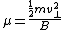is a constant of the motion to all orders in an expansion in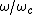
, where 
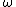is the rate of any changes experienced by the particle, e.g., due to collisions or due to temporal or spatial variations in the magnetic field. Consequently the magnetic moment remains nearly constant even for changes at rates approaching the gyrofrequency. When μ is constant, the perpendicular particle energy is proportional to B, so the particles can be heated by increasing B, but this is a 'one shot' deal because the field cannot be increased indefinitely.
There are some important situations in which the magnetic moment is not invariant:
,
where the integral is between the two turning points, is also an adiabatic invariant. This guarantees, for example, that a particle in the magnetosphere
moving around the Earth always returns to the same line of force. The adiabatic condition is violated in transit-time magnetic pumping, where the length of a magnetic mirror is oscillated at the bounce frequency, resulting in net heating.
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
that stays constant when changes occur slowly.
In thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, an adiabatic process is a change that occurs without heat flow, and slowly compared to the time to reach equilibrium. In an adiabatic process, the system is in equilibrium at all stages. Under these conditions, the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
is constant.
In mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, an adiabatic change is a slow deformation of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
, where the fractional rate of change
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
of the energy is much slower than the orbital frequency. The area enclosed by the different motions in phase space are the adiabatic invariants.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, an adiabatic change is one that occurs at a rate much slower than the difference in frequency between energy eigenstates. In this case, the energy states of the system do not make transitions, so that the quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
is an adiabatic invariant.
The old quantum theory
Old quantum theory
The old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
was formulated by equating the quantum number of a system with its classical adiabatic invariant. This determined the form of the Bohr-Sommerfeld quantization rule: the quantum number is the area in phase space of the classical orbit.
Thermodynamics
In thermodynamics, adiabatic changes are those that do not increase the entropy. They occur slowly, and allow heat flow only between objects at the same temperature. For isolated systems, an adiabatic change allows no heat to flow in or out.Adiabatic expansion of an ideal gas
If a container with an ideal gasIdeal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
is expanded instantaneously, the temperature of the gas doesn't change at all, because none of the molecules slow down. The molecules keep their kinetic energy, but now the gas occupies a bigger volume. If the container expands slowly, however, so that the ideal gas pressure law holds at any time, gas molecules lose energy at the rate that they do work on the expanding wall. The amount of work they do is the pressure times the area of the wall times the outward displacement, which is the pressure times the change in the volume of the gas:
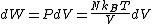
If no heat enters the gas, the energy in the gas molecules is decreasing by the same amount. By definition, a gas is ideal when its temperature is only a function of the internal energy per particle, not the volume. So
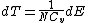
Where
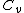is the specific heat at constant volume. When the change in energy is entirely due to work done on the wall, the change in temperature is given by: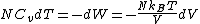This gives a differential relationship between the changes in temperature and volume, which can be integrated to find the invariant. The constant
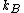is just a unit conversion factorNatural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
, which can be set equal to one:
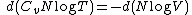
So
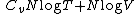
is an adiabatic invariant, which is related to the entropy
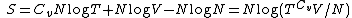
So entropy is an adiabatic invariant. The N log(N) term makes the entropy additive, so the entropy of two volumes of gas is the sum of the entropies of each one.
In a molecular interpretation, S is the logarithm of the phase space volume of all gas states with energy E(T) and volume V.
For a monatomic ideal gas, this can easily be seen by writing down the energy,
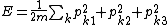
The different internal motions of the gas with total energy E define a sphere, the surface of a 3N-dimensional ball with radius
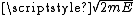. The volume of the sphere is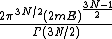,where
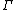is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
Since each gas molecule can be anywhere within the volume V, the volume in phase space occupied by the gas states with energy E is
.Since the N gas molecules are indistinguishable, the phase space volume is divided by
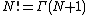, the number of permutations of N molecules.Using Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
for the gamma function, and ignoring factors that disappear in the logarithm after taking N large,
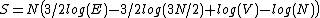
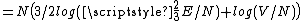
Since the specific heat of a monatomic gas is 3/2, this is the same as the thermodynamic formula for the entropy.
Wien's Law — adiabatic expansion of a box of light
For a box of radiation, ignoring quantum mechanics, the energy of a classical field in thermal equilibrium is infiniteUltraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
, since equipartition demands that each field mode has an equal energy on average and there are infinitely many modes. This is physically ridiculous, since it means that all energy leaks into high frequency electromagnetic waves over time.
Still, without quantum mechanics, there are some things that can be said about the equilibrium distribution from thermodynamics alone, because there is still a notion of adiabatic invariance that relates boxes of different size.
When a box is slowly expanded, the frequency of the light recoiling from the
wall can be computed from the Doppler shift. If the wall is not moving,
the light recoils at the same frequency. If the wall is moving slowly, the recoil frequency is only equal in the frame where the wall is stationary. In the frame where the wall is moving away from the light, the light coming in is bluer than the light coming out by twice the Doppler shift factor v/c.
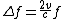
On the other hand, the energy in the light is also decreased when the wall is moving away, because the light is doing work on the wall by radiation pressure. Because the light is reflected, the pressure is equal to twice the momentum carried by light, which is E/c. The rate at which the pressure does work on the wall is found by multiplying by the velocity:
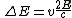
This means that the change in frequency of the light is equal to the work done on the wall by the radiation pressure. The light that is reflected is changed both in frequency and in energy by the same amount:
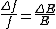
Since moving the wall slowly should keep a thermal distribution fixed, the probability that the light has energy E at frequency f must only be a function of E/f.
This function cannot be determined from thermodynamic reasoning alone, and Wien guessed at the form that was valid at high frequency. He supposed that the average energy in high frequency modes was suppressed by a Boltzmann-like factor. This is not the expected classical energy in the mode, which is
by equipartition, but a new and unjustified assumption that fit the high-frequency data.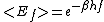When the expectation value is added over all modes in a cavity, this is Wien's distribution, and it describes the thermodynamic distribution of energy in a classical gas of photons. Wien's Law implicitly assumes that light is statistically composed of packets that change energy and frequency in the same way. The entropy of a Wein gas scales as the volume to the power N, where N is the number of packets. This led Einstein to suggest that light is composed of localizable particles with energy proportional to the frequency. Then the entropy of the Wien gas can be given a statistical interpretation as the number of possible positions that the photons can be in.
Classical mechanics — action variables
Suppose that a Hamiltonian is slowly time varying, for example, a one dimensional harmonic oscillator with a changing frequency.The action J of a classical orbit is the area
enclosed by the orbit in phase space.
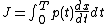
Since J is an integral over a full period, it is only a function of the energy. When
the Hamiltonian is constant in time and J is constant in time, the canonically conjugate variable
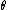increases in time at a steady rate.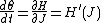So the constant H' can be used to change time derivatives along the orbit to partial derivatives with respect to
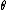at constant J. Differentiating the integral for J with respect to J gives an identity that fixes H':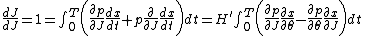The integrand is the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
of x and p. The Poisson bracket of two canonically conjugate quantities like x and p is equal to 1 in any canonical coordinate system. So
and H' is the inverse period. The variable
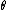increases by an equal amount in each period for all values of J— it is an angle-variable.Adiabatic Invariance of J
The Hamiltonian is a function of J only, and in the simple case of the Harmonic oscillator.
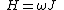
When H has no time dependence, J is constant. When H is slowly time varying, the
rate of change of J can be computed by reexpressing the integral for J
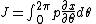
The time derivative of this quantity is
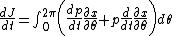
Replacing time derivatives with theta derivatives,
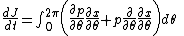
So as long as the coordinates J,
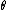do not change appreciably over one period, this expression can be integrated by parts to give zero. This meansthat for slow variations, there is no lowest order change in the area enclosed by
the orbit. This is the adiabatic invariance theorem— the action variables are adiabatic invariants.
For a harmonic oscillator, the area in phase space of an orbit at energy E is the area
of the ellipse of constant energy,
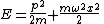
The x-radius of this ellipse is
, while the p-radius of the ellipse is 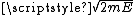. Multiplying, the area is 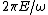. So if a pendulum is slowly drawn in, so that the frequency changes, the energy changes by a proportional amount.Old quantum theory
After Planck identified that Wien's law can be extended to all frequencies, even very low ones, by interpolating with the classical equipartition law for radiation, physicists wanted to understand the quantum behavior of other systems.The Planck radiation law quantized the motion of the field oscillators in units of energy proportional to the frequency:
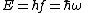
This is the only sensible quantization. The quantum can only depend on the energy/frequency by adiabatic invariance, and since the energy must be additive when putting boxes end to end, the levels must be equally spaced.
Einstein, followed by Debye, extended the domain of quantum mechanics by considering the sound modes in a solid as quantized oscillators
Einstein solid
The Einstein solid is a model of a solid based on two assumptions:* Each atom in the lattice is an independent 3D quantum harmonic oscillator* All atoms oscillate with the same frequency...
. This model explained why the specific heat of solids approached zero at low temperatures,
instead of staying fixed at
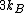as predicted by classical equipartitionEquipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
.
At the Solvay conference
Solvay Conference
The International Solvay Institutes for Physics and Chemistry, located in Brussels, were founded by the Belgian industrialist Ernest Solvay in 1912, following the historic invitation-only 1911 Conseil Solvay, the turning point in world physics...
, the question of quantizing other motions was raised, and Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
pointed out a problem. If you consider a quantum pendulum whose string is shortened very slowly, the quantum number of the pendulum cannot change because at no point is there a high enough frequency to cause a transition between the states. But the frequency of the pendulum changes when the string is shorter, so the quantum states change energy.
Einstein responded that for slow pulling, the frequency and energy of the pendulum both change but the ratio stays fixed. This is analogous to Wien's observation that under slow motion of the wall the energy to frequency ratio of reflected waves is constant. The conclusion was that the quantities to quantize must be adiabatic invariants.
This line of argument was extended by Sommerfeld into a general theory: the quantum number of an arbitrary mechanical system is given by the adiabatic action variable. Since the action variable in the harmonic oscillator is an integer, the general condition is:
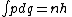
This condition was the foundation of the old quantum theory
Old quantum theory
The old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
, which was able to predict the qualitative behavior of atomic systems. The theory is inexact for small quantum numbers, since it mixes classical and quantum concepts. But it was a useful half-way step to the new quantum theory
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
.
Plasma physics
In plasma physics there are three adiabatic invariants of charged particle motion.The first adiabatic invariant, μ
The magnetic moment of a gyrating particle,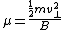,is a constant of the motion to all orders in an expansion in
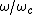, where 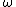is the rate of any changes experienced by the particle, e.g., due to collisions or due to temporal or spatial variations in the magnetic field. Consequently the magnetic moment remains nearly constant even for changes at rates approaching the gyrofrequency. When μ is constant, the perpendicular particle energy is proportional to B, so the particles can be heated by increasing B, but this is a 'one shot' deal because the field cannot be increased indefinitely.There are some important situations in which the magnetic moment is not invariant:
- Magnetic pumping: If the collision frequency is larger than the pump frequency, μ is no longer conserved. In particular, collisions allow net heating by transferring some of the perpendicular energy to parallel energy.
- Cyclotron heating: If B is oscillated at the cyclotron frequency, the condition for adiabatic invariance is violated and heating is possible. In particular, the induced electric field rotates in phase with some of the particles and continuously accelerates them.
- Magnetic cusps: The magnetic field at the center of a cusp vanishes, so the cyclotron frequency is automatically smaller than the rate of any changes. Thus the magnetic moment is not conserved and particles are scattered relatively easily into the loss coneMagnetic mirrorA magnetic mirror is a magnetic field configuration where the field strength changes when moving along a field line. The mirror effect results in a tendency for charged particles to bounce back from the high field region....
.
The second adiabatic invariant, J
The longitudinal invariant of a particle trapped in a magnetic mirror,,where the integral is between the two turning points, is also an adiabatic invariant. This guarantees, for example, that a particle in the magnetosphere
Magnetosphere
A magnetosphere is formed when a stream of charged particles, such as the solar wind, interacts with and is deflected by the intrinsic magnetic field of a planet or similar body. Earth is surrounded by a magnetosphere, as are the other planets with intrinsic magnetic fields: Mercury, Jupiter,...
moving around the Earth always returns to the same line of force. The adiabatic condition is violated in transit-time magnetic pumping, where the length of a magnetic mirror is oscillated at the bounce frequency, resulting in net heating.