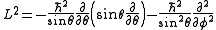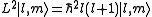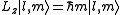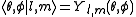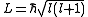In physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, angular momentum, moment of momentum, or rotational momentum is a conserved

Conservation law

In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....

 vector quantity that can be used to describe the overall state of a physical system. The angular momentum L of a particle with respect to some point of origin is
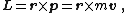
where r is the particle's position from the origin, is its linear momentum, and × denotes the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

.

The angular momentum of a system of particles (e.g. a rigid body) is the sum of angular momenta of the individual particles. For a rigid body

Rigid body

In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...

 rotating around an axis of symmetry (e.g. the fins of a ceiling fan), the angular momentum can be expressed as the product of the body's moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

 I (a measure of an object's resistance to changes in its rotation rate) and its angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

 ω:

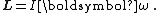
In this way, angular momentum is sometimes described as the rotational analog of linear momentum.

Angular momentum is conserved in a system where there is no net external torque

Torque

Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....

, and its conservation helps explain many diverse phenomena. For example, the increase in rotational speed of a spinning figure skater as the skater's arms are contracted is a consequence of conservation of angular momentum. The very high rotational rates of neutron star

Neutron star

A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...

s can also be explained in terms of angular momentum conservation. Moreover, angular momentum conservation has numerous applications in physics and engineering (e.g. the gyrocompass

Gyrocompass

A gyrocompass­ is a type of non-magnetic compass which bases on a fast-spinning disc and rotation of our planet to automatically find geographical direction...

).

Angular momentum in classical mechanics

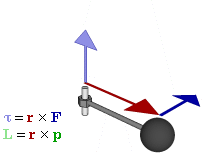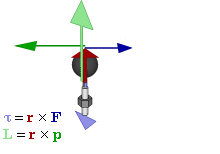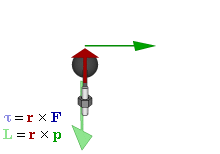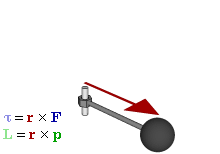
Definition

The angular momentum L of a particle about a given origin is defined as: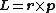


where r is the position vector of the particle relative to the origin, p is the linear momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

 of the particle, and × denotes the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

.

As seen from the definition, the derived SI units of angular momentum are newton meter second

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

s (N·m·s or kg·m²s⁻¹) or joule

Joule

The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...

 second

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

s. Because of the cross product, L is a pseudovector

Pseudovector

In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...

 perpendicular to both the radial vector r and the momentum vector p and it is assigned a sign by the right-hand rule

Right-hand rule

In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....

.

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

 of the object and its angular velocity vector:


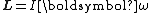
where I is the moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

 of the object (in general, a tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

 quantity), and ω is the angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

.

The angular momentum of a particle or rigid body in rectilinear motion (pure translation) is a vector with constant magnitude and direction. If the path of the particle or rigid body passes through the given origin, its angular momentum is zero.

Angular momentum is also known as moment

Moment (physics)

In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...

 of momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

.

Angular momentum of a collection of particles

If a system consists of several particles, the total angular momentum about a point can be obtained by adding (or integrating) all the angular momenta of the constituent particles.

Angular momentum simplified using the center of mass

It is very often convenient to consider the angular momentum of a collection of particles about their center of mass

Center of mass

In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

, since this simplifies the mathematics considerably. The angular momentum of a collection of particles is the sum of the angular momentum of each particle:


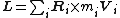
where R_i is the position vector of particle i from the reference point, m_i is its mass, and V_i is its velocity. The center of mass is defined by:


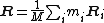
where the total mass of all particles is given by


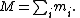
It follows that the velocity of the center of mass is


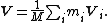
If we define r_i as the displacement of particle i from the center of mass, and v_i as the velocity of particle i with respect to the center of mass, then we have
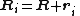   and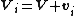   

and also
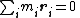   and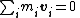   

so that the total angular momentum with respect to the center is


The first term is just the angular momentum of the center of mass. It is the same angular momentum one would obtain if there were just one particle of mass M moving at velocity V located at the center of mass. The second term is the angular momentum that is the result of the particles moving relative to their center of mass. This second term can be even further simplified if the particles form a rigid body

Rigid body

In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...

, in which case it is the product of moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

 and angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

 of the spinning motion (as above). The same result is true if the discrete point masses discussed above are replaced by a continuous distribution of matter.

Fixed axis of rotation

For many applications where one is only concerned about rotation around one axis, it is sufficient to discard the pseudovector nature of angular momentum, and treat it like a scalar where it is positive when it corresponds to a counter-clockwise rotation, and negative clockwise. To do this, just take the definition of the cross product and discard the unit vector, so that angular momentum becomes: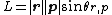


where θ_r,p is the angle between r and p measured from r to p; an important distinction because without it, the sign of the cross product would be meaningless. From the above, it is possible to reformulate the definition to either of the following:


where 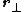is called the lever

Lever

In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...

 arm distance to p.

The easiest way to conceptualize this is to consider the lever arm distance to be the distance from the origin to the line that p travels along. With this definition, it is necessary to consider the direction of p (pointed clockwise or counter-clockwise) to figure out the sign of L. Equivalently:


where 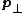is the component of p that is perpendicular to r. As above, the sign is decided based on the sense of rotation.

For an object with a fixed mass that is rotating about a fixed symmetry axis,
the angular momentum is expressed as the product of the moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

 of the object and its angular
velocity vector:


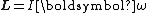
where I is the moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

 of the object (in general, a tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

 quantity) and ω is the angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

.

It is a misconception that angular momentum is always about the same axis as angular velocity. Sometime this may not be possible, in these cases the angular momentum component along the axis of rotation is the product of angular velocity and moment of inertia about the given axis of rotation.

As the kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

 K of a massive rotating body is given by


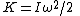
it is proportional to the square of the angular velocity.

Conservation of angular momentum

In a closed system angular momentum is constant. This conservation law mathematically follows from continuous directional symmetry of space (no direction in space is any different from any other direction). See Noether's theorem

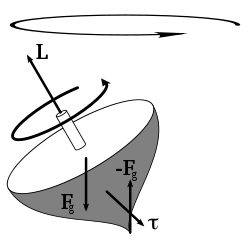
Noether's theorem

Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...

.

The time derivative of angular momentum is called torque

Torque

Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....

:


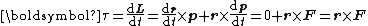
(The cross-product of velocity and momentum is zero, because these vectors are parallel.) So requiring the system to be "closed" here is mathematically equivalent to zero external torque acting on the system:


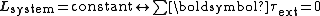
where 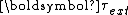is any torque applied to the system of particles.
It is assumed that internal interaction forces obey Newton's third law of motion

Newton's laws of motion

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...

 in its strong form, that is, that the forces between particles are equal and opposite and act along the line between the particles.

In orbits, the angular momentum is distributed between the spin of the planet itself and the angular momentum of its orbit:
;

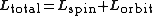If a planet is found to rotate slower than expected, then astronomers suspect that the planet is accompanied by a satellite, because the total angular momentum is shared between the planet and its satellite in order to be conserved.
The conservation of angular momentum is used extensively in analyzing what is called central force motion. If the net force on some body is directed always toward some fixed point, the center, then there is no torque on the body with respect to the center, and so the angular momentum of the body about the center is constant. Constant angular momentum is extremely useful when dealing with the orbit

Orbit

In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...

s of planet

Planet

A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...

s and satellite

Satellite

In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....

s, and also when analyzing the Bohr model

Bohr model

In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...

 of the atom

Atom

The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...

.

The conservation of angular momentum explains the angular acceleration of an ice skater as she brings her arms and legs close to the vertical axis of rotation. By bringing part of mass of her body closer to the axis she decreases her body's moment of inertia. Because angular momentum is constant in the absence of external torques, the angular velocity (rotational speed) of the skater has to increase.

The same phenomenon results in extremely fast spin of compact stars (like white dwarf

White dwarf

A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...

s, neutron star

Neutron star

A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...

s and black hole

Black hole

A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...

s) when they are formed out of much larger and slower rotating stars (indeed, decreasing the size of object 10⁴ times results in increase of its angular velocity by the factor 10⁸).

The conservation of angular momentum in Earth–Moon system

Lunar theory

Lunar theory attempts to account for the motions of the Moon. There are many irregularities in the Moon's motion, and many attempts have been made over a long history to account for them. After centuries of being heavily problematic, the lunar motions are nowadays modelled to a very high degree...

 results in the transfer of angular momentum from Earth to Moon (due to tidal torque the Moon exerts on the Earth). This in turn results in the slowing down of the rotation rate of Earth (at about 42 nsec/day), and in gradual increase of the radius of Moon's orbit (at ~4.5 cm/year rate).

Angular momentum in relativistic mechanics

In modern (late 20th century) theoretical physics, angular momentum is described using a different formalism. Under this formalism, angular momentum is the 2-form Noether charge associated with rotational invariance (As a result, angular momentum is not conserved for general curved spacetimes

Curved space

Curved space often refers to a spatial geometry which is not “flat” where a flat space is described by Euclidean geometry. Curved spaces can generally be described by Riemannian geometry though some simple cases can be described in other ways. Curved spaces play an essential role in General...

, unless it happens to be asymptotically rotationally invariant). For a system of point particles without any intrinsic angular momentum (see below), it turns out to be


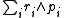
(Here, the wedge product is used.).

In the language of four-vector

Four-vector

In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...

s and tensors the angular momentum of a particle in relativistic mechanics is expressed as an antisymmetric tensor of second order

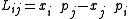
Angular momentum in quantum mechanics

In quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

, angular momentum is quantized

Quantization (physics)

In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...

 – that is, it cannot vary continuously, but only in "quantum leaps

Quantum number

Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...

" between certain allowed values. The orbital angular momentum of a subatomic particle, that is due to its motion through space, is always a whole-number multiple of 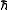("h-bar," known as the reduced Planck's constant), which has an appropriate dimension energy·time, or length·momentum. Furthermore, experiments show that most subatomic particles have a permanent, built-in angular momentum, which is not due to their motion through space. This spin

Spin (physics)

In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...

 angular momentum comes in units of 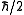. For example, an electron standing at rest has an angular momentum of .

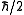Basic definition

The classical definition of angular momentum as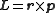 depends on six numbers: , , 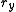, , 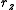, 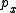and 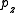. Translating this into quantum-mechanical terms, the Heisenberg uncertainty principle

Uncertainty principle

In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...

 tells us that it is not possible for all six of these numbers to be measured simultaneously with arbitrary precision. Therefore, there are limits to what can be known or measured about a particle's angular momentum. It turns out that the best that one can do is to simultaneously measure both the angular momentum vector's magnitude and its component along one axis.

Mathematically, angular momentum in quantum mechanics is defined like momentum – not as a quantity but as an operator

Operator (physics)

In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....

 on the wave function:


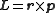
where r and p are the position and momentum operators respectively. In particular, for a single particle with no electric charge

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

 and no spin, the angular momentum operator

Angular momentum operator

In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...

 can be written in the position basis as


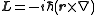
where 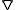is the vector differential operator del

Del

In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...

 (also called "nabla

Nabla symbol

right|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...

"). This orbital angular momentum operator is the most commonly encountered form of the angular momentum operator, though not the only one. It satisfies the following canonical commutation relation

Canonical commutation relation

In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...

s:,

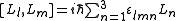where

• ε_lmn is the (antisymmetric) Levi-Civita symbol
  Levi-Civita symbol
  The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
  
  ,
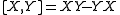• is the commutator
  Commutator
  In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
  
  .

From this follows

Since,

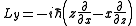
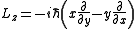
it follows, for example,

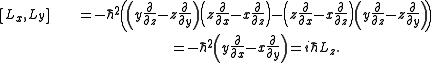
Addition of quantized angular momenta

Given a quantized total angular momentum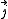 which is the sum of two individual quantized angular momenta 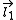and ,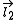


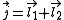
the quantum number

Quantum number

Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...

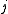  associated with its magnitude can range from 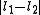to 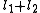in integer steps
where 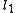and 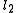are quantum numbers corresponding to the magnitudes of the individual angular momenta.

Angular momentum as a generator of rotations

If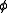 is the angle around a specific axis, for example the azimuthal angle around the z axis, then the angular momentum along this axis is the generator

Noether's theorem

Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...

 of rotations around this axis:

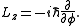
The eigenfunction

Eigenfunction

In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...

s of L_z are therefore , and since 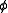has a period of 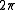, m_l must be an integer.

For a particle with a spin

Spin (physics)

In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...

 S, this takes into account only the angular dependence of the location of the particle, for example its orbit in an atom. It is therefore known as orbital angular momentum

Angular momentum operator

In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...

. However, when one rotates the system, one also changes the spin. Therefore the total angular momentum, which is the full generator of rotations, is

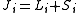
Being an angular momentum, J satisfies the same commutation relations as L, as will be explained below, namely
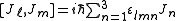
from which follows

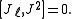
Acting with J on the wavefunction

Wavefunction

Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...

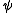  of a particle generates a rotation:
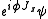is the wavefunction 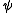rotated around the z axis by an angle 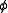. For an infinitesmal rotation by an angle 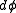, the rotated wavefunction is 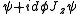. This is similarly true for rotations around any axis.

In a charged particle the momentum gets a contribution from the electromagnetic field, and the angular momenta L and J change accordingly.

If the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

 is invariant under rotations, as in spherically symmetric problems, then according to Noether's theorem

Noether's theorem

Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...

, it commutes

Commutator

In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...

 with the total angular momentum. So the total angular momentum is a conserved quantity

Conserved quantity

In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...

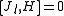
Since angular momentum is the generator of rotations, its commutation relations follow the commutation relations of the generators of the three-dimensional rotation group

Rotation group

In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...

 SO

Orthogonal group

In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...

(3). This is why J always satisfies these commutation relations. In d dimensions, the angular momentum will satisfy the same commutation relations as the generators of the d-dimensional rotation group SO(d).

SO(3) has the same Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

 (i.e. the same commutation relations) as SU(2). Generators of SU(2) can have half-integer eigenvalues, and so can m_j. Indeed for fermion

Fermion

In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....

s the spin S and total angular momentum J are half-integer. For d=3, in fact, j and m_j always are either integers or half-integers.

Technically, this is because the universal cover of SO(3) is isomorphic to SU(2), and the representations of the latter

Representation theory of SU(2)

In the study of the representation theory of Lie groups, the study of representations of SU is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group and a non-abelian group...

 are fully known. J_i span the Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

 and J² is the Casimir invariant

Casimir invariant

In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...

, and it can be shown that if the eigenvalues of J_z and J² are m_j and j(j+1) then m_j and j are both integer multiples of one-half. j is non-negative and m_j takes values between −j and j.

Relation to spherical harmonics

Angular momentum operators usually occur when solving a problem with spherical symmetry in spherical coordinates. Then, the angular momentum in space representation is:

When solving to find eigenstates of this operator, we obtain the following

where

are the spherical harmonic

Spherical Harmonic

Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...

s.

Thus, a particle whose wave function is the spherical harmonic 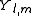has an orbital angular momentum

with a z-component

Angular momentum in electrodynamics

When describing the motion of a charged particle in the presence of an electromagnetic field

Electromagnetic field

An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...

, the canonical momentum p is not gauge invariant. As a consequence, the canonical angular momentum 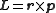is not gauge invariant either. Instead, the momentum that is physical, the so-called kinetic momentum, is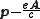


where is the electric charge

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

, c the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

 and A the vector potential. Thus, for example, the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

 of a charged particle of mass m in an electromagnetic field is then


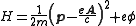
where 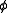is the scalar potential

Electric potential

In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...

. This is the Hamiltonian that gives the Lorentz force law. The gauge-invariant angular momentum, or "kinetic angular momentum" is given by


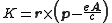
The interplay with quantum mechanics is discussed further in the article on canonical commutation relation

Canonical commutation relation

In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...

s.

See also

• Angular momentum coupling
  Angular momentum coupling
  In quantum mechanics, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin-orbit interaction, in which case the...
  
  
• Angular momentum of light
  Angular momentum of light
  The angular momentum of light is a vector quantity that expresses the amount of dynamical rotation present in the electromagnetic field of the light. Indeed, a beam of light, while traveling approximately in a straight line, can also be rotating around its own axis...
  
  
• Angular momentum operator
  Angular momentum operator
  In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
  
  
• Areal velocity
  Areal velocity
  Areal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
  
  
• Balancing machine
  Balancing Machine
  A balancing machine is a measuring tool used for balancing rotating machine parts such as rotors for electric motors, fans, turbines, disc brakes, disc drives, propellers and pumps. The machine usually consists of two rigid pedestals, with suspension and bearings on top supporting a mounting...
  
  
• Control moment gyroscope
  Control moment gyroscope
  A control momentum gyroscope is an attitude control device generally used in spacecraft attitude control systems. A CMG consists of a spinning rotor and one or more motorized gimbals that tilt the rotor’s angular momentum. As the rotor tilts, the changing angular momentum causes a gyroscopic...
  
  
• Falling cat problem
  Falling cat problem
  The falling cat problem consists of explaining the underlying physics behind the common observation of the cat righting reflex: how a free-falling cat can turn itself right-side-up as it falls, no matter which way up it was initially, without violating the law of conservation of angular...
  
  
• List of moments of inertia
• Moment of inertia
  Moment of inertia
  In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
  
  
• Noether's theorem
  Noether's theorem
  Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
  
  
• Precession
  Precession
  Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
  
  
• Relative angular momentum
• Rigid rotor
  Rigid rotor
  The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
  
  
• Rotational energy
  Rotational energy
  The rotational energy or angular kinetic energy is the kinetic energy due to the rotation of an object and is part of its total kinetic energy...
  
  
• Spatial quantization
  Spatial quantization
  In quantum mechanics, spatial quantization is the quantization of angular momentum in three-dimensional space. It results from the fact that the angular momentum of a rigid rotor is expressed in three dimensions, and is quantized....
  
  
• Specific relative angular momentum
  Specific relative angular momentum
  The specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
  
  
• Spin (physics)
  Spin (physics)
  In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
  
  
• Yrast
  Yrast
  Yrast is a technical term in nuclear physics that refers to a state of a nucleus with a minimum of energy for a given angular momentum. Yr is a Swedish adjective derived from the Old Norse hvirfla, the same root as the English whirl...
  
  

External links

• Conservation of Angular Momentum - a chapter from an online textbook
• Angular Momentum in a Collision Process - derivation of the three dimensional case