
Physical constant
Encyclopedia
A physical constant is a physical quantity
that is generally believed to be both universal in nature and constant
in time. It can be contrasted with a mathematical constant
, which is a fixed numerical value but does not directly involve any physical measurement.
There are many physical constants in science, some of the most widely recognized being the speed of light
in vacuum c, the gravitational constant
G, Planck's constant h, the electric constant
ε0, and the elementary charge
e. Physical constants can take many dimensional
forms: the speed of light signifies a maximum speed
limit of the universe
and is expressed dimensionally as length
divided by time
; while the fine-structure constant
α, which characterizes the strength of the electromagnetic interaction, is dimensionless.
indicated by any physical constant does not depend on the unit system used to express the quantity, the numerical values of dimensionful physical constants do depend on the unit used. Therefore, these numerical values (such as 299,792,458 for the constant speed of light
c expressed in units of meters per second) are not values that a theory of physics can be expected to predict.
Because their units cancel, ratios of like-dimensioned physical constants do not depend on unit systems in this way, so they are pure dimensionless numbers whose values a future theory of physics could conceivably hope to predict. Additionally, all equations describing laws of physics
can be expressed without dimensional physical constants via a process known as nondimensionalisation, but the dimensionless constants will remain. Thus, theoretical physicists tend to regard these dimensionless quantities as fundamental physical constants.
However, the term fundamental physical constant is also used in other ways. For example, the National Institute of Standards and Technology uses the term to refer to any universal physical quantity believed to be constant, such as the speed of light, c, and the gravitational constant
G.
The fine-structure constant
α is probably the best known dimensionless fundamental physical constant. Many attempts have been made to derive its value (currently measured at about 1/137.035999) from theory, but so far none have succeeded. The same holds for the dimensionless ratios of masses of fundamental particles (the most apparent is mp/me
, approximately 1836.152672). With the development of quantum chemistry
in the 20th century, however, a vast number of previously inexplicable dimensionless physical constants were successfully computed from theory. As such, some theoretical physicists still hope for continued progress in explaining the values of other dimensionless physical constants.
It is known that the universe would be very different
if these constants took values significantly different from those we observe. For example, a few percent change in the value of the fine structure constant would be enough to eliminate stars like our Sun. This has prompted attempts at anthropic
explanations of the values of some of the dimensionless fundamental physical constants.
in 1937, some scientists have speculated that physical constants may actually decrease in proportion to the age of the universe. Scientific experiments have not yet pinpointed any definite evidence that this is the case, although they have placed upper bounds on the maximum possible relative change per year at very small amounts (roughly 10−17 per year for the fine structure constant α and 10−11 for the gravitational constant G).
It is currently disputed whether any changes in dimensional physical constants such as G, c, ħ, or ε0 are operationally meaningful; however, a sufficient change in a dimensionless constant such as α is generally agreed to be something that would definitely be noticed. If a measurement indicated that a dimensional physical constant had changed, this would be the result or interpretation of a more fundamental dimensionless constant changing, which is the salient metric. From :
s had sufficiently different values, our universe would be so radically different that intelligent life would probably not have emerged, and that our universe therefore seems to be fine-tuned
for intelligent life. The anthropic principle states a logical truism
: the fact of our existence as intelligent beings who can measure physical constants requires those constants to be such that beings like us can exist. There are a variety of interpretations of the constants' values, including that of a divine creator
(the apparent fine-tuning is actual and intentional), or that ours is one universe of many in a multiverse
(e.g. the Many-worlds interpretation
of quantum mechanics
), or even that a universe without the capacity for conscious beings cannot exist.
, it is possible to combine dimensional universal physical constants to define a system of units of measurement
that has no reference to any human construct. Depending on the choice and arrangement of constants used, the resulting natural units may have useful physical meaning. For example, Planck units
, shown below, use c
, G
, ħ
, ε0
and kB in such a manner to derive units relevant to unified theories such as quantum gravity
.
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
that is generally believed to be both universal in nature and constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
in time. It can be contrasted with a mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
, which is a fixed numerical value but does not directly involve any physical measurement.
There are many physical constants in science, some of the most widely recognized being the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in vacuum c, the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G, Planck's constant h, the electric constant
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
ε0, and the elementary charge
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
e. Physical constants can take many dimensional
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
forms: the speed of light signifies a maximum speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
limit of the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
and is expressed dimensionally as length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
divided by time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
; while the fine-structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
α, which characterizes the strength of the electromagnetic interaction, is dimensionless.
Dimensional and dimensionless physical constants
Whereas the physical quantityPhysical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
indicated by any physical constant does not depend on the unit system used to express the quantity, the numerical values of dimensionful physical constants do depend on the unit used. Therefore, these numerical values (such as 299,792,458 for the constant speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c expressed in units of meters per second) are not values that a theory of physics can be expected to predict.
Because their units cancel, ratios of like-dimensioned physical constants do not depend on unit systems in this way, so they are pure dimensionless numbers whose values a future theory of physics could conceivably hope to predict. Additionally, all equations describing laws of physics
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
can be expressed without dimensional physical constants via a process known as nondimensionalisation, but the dimensionless constants will remain. Thus, theoretical physicists tend to regard these dimensionless quantities as fundamental physical constants.
However, the term fundamental physical constant is also used in other ways. For example, the National Institute of Standards and Technology uses the term to refer to any universal physical quantity believed to be constant, such as the speed of light, c, and the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G.
The fine-structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
α is probably the best known dimensionless fundamental physical constant. Many attempts have been made to derive its value (currently measured at about 1/137.035999) from theory, but so far none have succeeded. The same holds for the dimensionless ratios of masses of fundamental particles (the most apparent is mp/me
Proton-to-electron mass ratio
In physics, the proton-to-electron mass ratio, μ or β, is simply the rest mass of the proton divided by that of the electron...
, approximately 1836.152672). With the development of quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
in the 20th century, however, a vast number of previously inexplicable dimensionless physical constants were successfully computed from theory. As such, some theoretical physicists still hope for continued progress in explaining the values of other dimensionless physical constants.
It is known that the universe would be very different
Fine-tuned universe
The fine-tuned universe is the proposition that the conditions that allow life in the Universe can only occur when certain universal fundamental physical constants lie within a very narrow range, so that if any of several fundamental constants were only slightly different the universe would be...
if these constants took values significantly different from those we observe. For example, a few percent change in the value of the fine structure constant would be enough to eliminate stars like our Sun. This has prompted attempts at anthropic
Anthropic principle
In astrophysics and cosmology, the anthropic principle is the philosophical argument that observations of the physical Universe must be compatible with the conscious life that observes it. Some proponents of the argument reason that it explains why the Universe has the age and the fundamental...
explanations of the values of some of the dimensionless fundamental physical constants.
How constant are the physical constants?
Beginning with Paul DiracPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
in 1937, some scientists have speculated that physical constants may actually decrease in proportion to the age of the universe. Scientific experiments have not yet pinpointed any definite evidence that this is the case, although they have placed upper bounds on the maximum possible relative change per year at very small amounts (roughly 10−17 per year for the fine structure constant α and 10−11 for the gravitational constant G).
It is currently disputed whether any changes in dimensional physical constants such as G, c, ħ, or ε0 are operationally meaningful; however, a sufficient change in a dimensionless constant such as α is generally agreed to be something that would definitely be noticed. If a measurement indicated that a dimensional physical constant had changed, this would be the result or interpretation of a more fundamental dimensionless constant changing, which is the salient metric. From :
[An] important lesson we learn from the way that pure numbers like α define the world is what it really means for worlds to be different. The pure number we call the fine structure constant and denote by α is a combination of the electron charge, e, the speed of light, c, and Planck's constant, h. At first we might be tempted to think that a world in which the speed of light was slower would be a different world. But this would be a mistake. If c, h, and e were all changed so that the values they have in metric (or any other) units were different when we looked them up in our tables of physical constants, but the value of α remained the same, this new world would be observationally indistinguishable from our world. The only thing that counts in the definition of worlds are the values of the dimensionless constants of Nature. If all masses were doubled in value you cannot tell because all the pure numbers defined by the ratios of any pair of masses are unchanged.
Anthropic principle
Some physicists have explored the notion that if the dimensionless physical constantDimensionless physical constant
In physics, a dimensionless physical constant is a universal physical constant that is dimensionless - having no unit attached, so its numerical value is the same under all possible systems of units...
s had sufficiently different values, our universe would be so radically different that intelligent life would probably not have emerged, and that our universe therefore seems to be fine-tuned
Fine-tuned universe
The fine-tuned universe is the proposition that the conditions that allow life in the Universe can only occur when certain universal fundamental physical constants lie within a very narrow range, so that if any of several fundamental constants were only slightly different the universe would be...
for intelligent life. The anthropic principle states a logical truism
Truism
A truism is a claim that is so obvious or self-evident as to be hardly worth mentioning, except as a reminder or as a rhetorical or literary device and is the opposite of falsism....
: the fact of our existence as intelligent beings who can measure physical constants requires those constants to be such that beings like us can exist. There are a variety of interpretations of the constants' values, including that of a divine creator
Intelligent design
Intelligent design is the proposition that "certain features of the universe and of living things are best explained by an intelligent cause, not an undirected process such as natural selection." It is a form of creationism and a contemporary adaptation of the traditional teleological argument for...
(the apparent fine-tuning is actual and intentional), or that ours is one universe of many in a multiverse
Multiverse
The multiverse is the hypothetical set of multiple possible universes that together comprise all of reality.Multiverse may also refer to:-In fiction:* Multiverse , the fictional multiverse used by DC Comics...
(e.g. the Many-worlds interpretation
Many-worlds interpretation
The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
), or even that a universe without the capacity for conscious beings cannot exist.
Table of adopted values
| Quantity | Symbol | Value (SI Si Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system... units) |
Relative Standard Uncertainty | |
|---|---|---|---|---|
| conventional value of Josephson constant |  |
4.835 979 × 1014 Hz·V−1 | defined | |
| conventional value of von Klitzing constant | 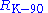 |
25 812.807 Ω | defined | |
| molar mass | constant Molar mass constant The molar mass constant, symbol Mu, is a physical constant which relates atomic weight and molar mass. Its value is defined to be 1 g/mol in SI units.... |
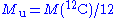 |
1 × 10−3 kg·mol−1 | defined |
| of carbon-12 Carbon-12 Carbon-12 is the more abundant of the two stable isotopes of the element carbon, accounting for 98.89% of carbon; it contains 6 protons, 6 neutrons, and 6 electrons.... |
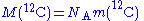 |
1.2 × 10−2 kg·mol−1 | defined | |
| standard acceleration of gravity Gravitation Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped... (gee Standard gravity Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about... , free-fall Free-fall Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward... on Earth) |
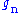 |
9.806 65 m·s−2 | defined | |
| standard atmosphere Atmosphere (unit) The standard atmosphere is an international reference pressure defined as 101325 Pa and formerly used as unit of pressure. For practical purposes it has been replaced by the bar which is 105 Pa... |
 |
101 325 Pa | defined | |
Natural units
Using dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
, it is possible to combine dimensional universal physical constants to define a system of units of measurement
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
that has no reference to any human construct. Depending on the choice and arrangement of constants used, the resulting natural units may have useful physical meaning. For example, Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
, shown below, use c
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, G
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, ħ
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, ε0
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
and kB in such a manner to derive units relevant to unified theories such as quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
.
External links
- Sixty Symbols, University of Nottingham
- IUPAC - Gold Book

