
Perturbation theory
Encyclopedia
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem. Perturbation theory is applicable if the problem at hand can be formulated by adding a "small" term to the mathematical description of the exactly solvable problem.
Perturbation theory leads to an expression for the desired solution in terms of a formal power series in some "small" parameter that quantifies the deviation from the exactly solvable problem. The leading term in this power series is the solution of the exactly solvable problem, while further terms describe the deviation in the solution, due to the deviation from the initial problem. Formally, we have for the approximation to the full solution A, a series in the small parameter (here called ), like the following:
), like the following:

In this example,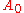 would be the known solution to the exactly solvable initial problem and
would be the known solution to the exactly solvable initial problem and 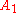 ,
,  ... represent the higher-order terms which may be found iteratively by some systematic procedure. For small
... represent the higher-order terms which may be found iteratively by some systematic procedure. For small  these higher-order terms in the series become successively smaller. An approximate "perturbation solution" is obtained by truncating the series, usually by keeping only the first two terms, the initial solution and the "first-order" perturbation correction:
these higher-order terms in the series become successively smaller. An approximate "perturbation solution" is obtained by truncating the series, usually by keeping only the first two terms, the initial solution and the "first-order" perturbation correction:

. The earliest use of what would now be called perturbation theory was to deal with the otherwise unsolvable mathematical problems of celestial mechanics
: Newton
's solution for the orbit of the Moon
, which moves noticeably differently from a simple Keplerian ellipse
because of the competing gravitation of the Earth
and the Sun
.
Perturbation methods start with a simplified form of the original problem, which is simple enough to be solved exactly. In celestial mechanics
, this is usually a Keplerian ellipse
. Under non relativistic gravity, an ellipse is exactly correct when there are only two gravitating bodies (say, the Earth
and the Moon
) but not quite correct when there are three or more objects (say, the Earth
, Moon
, Sun
, and the rest of the solar system
).
The solved, but simplified problem is then "perturbed" to make the conditions that the perturbed solution actually satisfies closer to the real problem, such as including the gravitational attraction of a third body (the Sun
). The "conditions" are a formula (or several) that represent reality, often something arising from a physical law like Newton's second law, the force-acceleration equation:
In the case of the example, the force is calculated based on the number of gravitationally relevant bodies; the acceleration
is calculated based on the number of gravitationally relevant bodies; the acceleration  is obtained, using calculus, from the path of the Moon
is obtained, using calculus, from the path of the Moon
in its orbit. Both of these come in two forms: approximate values for force and acceleration, which result from simplifications, and hypothetical exact values for force and acceleration, which would require the complete answer to calculate.
The slight changes that result from accommodating the perturbation, which themselves may have been simplified yet again, are used as corrections to the approximate solution. Because of simplifications introduced along every step of the way, the corrections are never perfect, and the conditions met by the corrected solution do not perfectly match the equation demanded by reality, but even one cycle of corrections often provides a remarkably better approximate answer to what the real solution should be.
There is no requirement to stop at only one cycle of corrections. A partially corrected solution can be re-used as the new starting point for yet another cycle of perturbations and corrections. In principle, cycles of finding increasingly better corrections could go on indefinitely. In practice, one typically stops at one or two cycles of corrections, due to exhaustion. The usual difficulty with the method is that the corrections progressively make the new solutions very much more complicated, so each cycle is much more difficult to manage than the previous cycle of corrections. Isaac Newton
is reported to have said, regarding the problem of the Moon
's orbit, that "It causeth my head to ache."
This general procedure is a widely used mathematical tool in advanced sciences and engineering: start with a simplified problem and gradually add corrections that make the formula that the corrected problem matches closer and closer to the formula that represents reality. It is the natural extension to mathematical functions
of the "guess, check, and fix" method used anciently with numbers.
an algebraic equation,
a differential equation
(e.g., the equations of motion in celestial mechanics
or a wave equation
),
a free energy
(in statistical mechanics
),
a Hamiltonian
operator (in quantum mechanics
).
Examples for the kind of solution to be found perturbatively:
the solution of the equation (e.g., the trajectory
of a particle),
the statistical average
of some
physical quantity (e.g., average magnetization),
the ground state
energy of a quantum mechanical
problem.
Examples for the exactly solvable problems to start with:
linear equation
s, including linear equations of motion
(harmonic oscillator
, linear wave equation), statistical or quantum-mechanical systems of
non-interacting particles (or in general, Hamiltonians or free
energies containing only terms quadratic in all degrees of freedom).
Examples of "perturbations" to deal with:
Nonlinear contributions to the equations of motion, interaction
s
between particles, terms of higher powers in the Hamiltonian/Free Energy.
For physical problems involving interactions between particles,
the terms of the perturbation series may be displayed (and
manipulated) using Feynman diagram
s.
, where the theory of epicycles was used to make small corrections to the predicted paths of planets. Curiously, it was the need for more and more epicycles that eventually led to the 16th century Copernican revolution
in the understanding of planetary orbits. The development of basic perturbation theory for differential equation
s was fairly complete by the middle of the 19th century. It was at that time that Charles-Eugène Delaunay
was studying the perturbative expansion for the Earth-Moon-Sun system, and discovered the so-called "problem of small denominators". Here, the denominator appearing in the n'th term of the perturbative expansion could become arbitrarily small, causing the n'th correction to be as large or larger than the first-order correction. At the turn of the 20th century, this problem led Henri Poincaré
to make one of the first deductions of the existence of chaos
, or what is prosaically called the "butterfly effect
": that even a very small perturbation can have a very large effect on a system.
Perturbation theory saw a particularly dramatic expansion and evolution with the arrival of quantum mechanics
. Although perturbation theory was used in the semi-classical theory of the Bohr atom, the calculations were monstrously complicated, and subject to somewhat ambiguous interpretation. The discovery of Heisenberg's matrix mechanics
allowed a vast simplification of the application of perturbation theory. Notable examples are the Stark effect
and the Zeeman effect
, which have a simple enough theory to be included in standard undergraduate textbooks in quantum mechanics. Other early applications include the fine structure
and the hyperfine structure
in the hydrogen atom
.
In modern times, perturbation theory underlies much of quantum chemistry
and quantum field theory
. In chemistry, perturbation theory was used to obtain the first solutions for the helium atom
.
In the middle of the 20th century, Richard Feynman
realized that the perturbative expansion could be given a dramatic and beautiful graphical representation in terms of what are now called Feynman diagrams. Although originally applied only in quantum field theory
, such diagrams now find increasing use in any area where perturbative expansions are studied.
A partial resolution of the small-divisor problem was given by the statement of the KAM theorem in 1954. Developed by Andrey Kolmogorov
, Vladimir Arnold
and Jürgen Moser
, this theorem stated the conditions under which a system of partial differential equations will have only mildly chaotic behaviour under small perturbations.
In the late 20th century, broad dissatisfaction with perturbation theory in the quantum physics community, including not only the difficulty of going beyond second order in the expansion, but also questions about whether the perturbative expansion is even convergent, has led to a strong interest in the area of non-perturbative analysis, that is, the study of exactly solvable models. The prototypical model is the Korteweg–de Vries equation
, a highly non-linear equation for which the interesting solutions, the soliton
s, cannot be reached by perturbation theory, even if the perturbations were carried out to infinite order. Much of the theoretical work in non-perturbative analysis goes under the name of quantum group
s and non-commutative geometry.
), in which case extra care must be taken, and the theory is slightly more difficult.
to the first order. To keep the exposition simple, a crucial assumption is made: that the solutions to the unperturbed system are not degenerate
, so that the perturbation series can be inverted. There are ways of dealing with the degenerate (or singular
) case; these require extra care.
Suppose one wants to solve a differential equation of the form
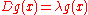
where D is some specific differential operator
, and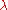 is an eigenvalue. Many problems involving ordinary or partial differential equations can be cast in this form. It is presumed that the differential operator can be written in the form
is an eigenvalue. Many problems involving ordinary or partial differential equations can be cast in this form. It is presumed that the differential operator can be written in the form

where is presumed to be small, and that furthermore, the complete set of solutions for
is presumed to be small, and that furthermore, the complete set of solutions for 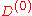 are known. That is,one has a set of solutions
are known. That is,one has a set of solutions  , labelled by some arbitrary index n, such that
, labelled by some arbitrary index n, such that
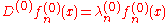 .
.
Furthermore, one assumes that the set of solutions form an orthonormal set:
form an orthonormal set:

with the Kronecker delta function.
the Kronecker delta function.
To zeroth order, one expects that the solutions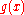 are then somehow "close" to one of the unperturbed solutions
are then somehow "close" to one of the unperturbed solutions  . That is,
. That is,
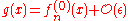
and
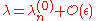 .
.
where denotes the relative size, in big-O notation, of the perturbation. To solve this problem, one assumes that the solution
denotes the relative size, in big-O notation, of the perturbation. To solve this problem, one assumes that the solution 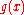 can be written as a linear combination of the
can be written as a linear combination of the  :
:
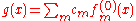
with all of the constants except for n, where
except for n, where  . Substituting this last expansion into the differential equation, taking the inner product of the result with
. Substituting this last expansion into the differential equation, taking the inner product of the result with 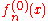 , and making use of orthogonality, one obtains
, and making use of orthogonality, one obtains
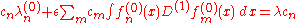
This can be trivially rewritten as a simple linear algebra
problem of finding the eigenvalue of a matrix
, where
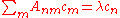
where the matrix elements are given by
are given by
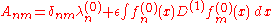
Rather than solving this full matrix equation, one notes that, of all the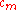 in the linear equation, only one, namely
in the linear equation, only one, namely  , is not small. Thus, to the first order in
, is not small. Thus, to the first order in  , the linear equation may be solved trivially as
, the linear equation may be solved trivially as
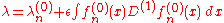
since all of the other terms in the linear equation are of order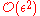 . The above gives the solution of the eigenvalue to first order in perturbation theory.
. The above gives the solution of the eigenvalue to first order in perturbation theory.
The function to first order is obtained through similar reasoning. Substituting
to first order is obtained through similar reasoning. Substituting
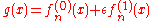
so that
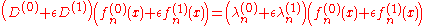
gives an equation for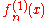 . It may be solved integrating with the partition of unity
. It may be solved integrating with the partition of unity

to give

which gives the exact solution to the perturbed differential equation to the first order in the perturbation .
.
Several important observations can be made about the form of this solution. First, the sum over functions with differences of eigenvalues in the denominator resembles the resolvent in Fredholm theory
. This is no accident; the resolvent acts essentially as a kind of Green's function
or propagator
, passing the perturbation along. Higher-order perturbations resemble this form, with an additional sum over a resolvent appearing at each order.
The form of this solution is sufficient to illustrate the idea behind the small-divisor problem. If, for whatever reason, two eigenvalues are close so that difference become small, the corresponding term in the sum will become disproportionately large. In particular, if this happens in higher-order terms, the high-order perturbation may become as large or larger in magnitude than the first-order perturbation. Such a situation calls into question the validity of doing a perturbation to begin with. This can be understood to be a fairly catastrophic situation; it is frequently encountered in chaotic dynamical systems
become small, the corresponding term in the sum will become disproportionately large. In particular, if this happens in higher-order terms, the high-order perturbation may become as large or larger in magnitude than the first-order perturbation. Such a situation calls into question the validity of doing a perturbation to begin with. This can be understood to be a fairly catastrophic situation; it is frequently encountered in chaotic dynamical systems
, and requires the development of techniques other than perturbation theory to solve the problem.
Curiously, the situation is not at all bad if two or more eigenvalues are exactly equal. This case is referred to as singular
or degenerate perturbation theory. The degeneracy of eigenvalues indicates that the unperturbed system has some sort of symmetry
, and that the generators of the symmetry commute with the unperturbed differential operator. Typically, the perturbing term does not possess the symmetry; one says the perturbation lifts or breaks the degeneracy. In this case, the perturbation can still be performed; however, one must be careful to work in a basis for the unperturbed states so that these map one-to-one to the perturbed states, rather than being a mixture.
 :
:

For the initial problem with , the solution is
, the solution is  . For small
. For small  the lowest-order approximation may be found by inserting the ansatz
the lowest-order approximation may be found by inserting the ansatz

into the equation and demanding the equation to be fulfilled up to terms that involve powers of higher than the first. This yields
higher than the first. This yields 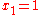 . In the same way, the higher orders may be found. However, even in this simple example it may be observed that for (arbitrarily) small
. In the same way, the higher orders may be found. However, even in this simple example it may be observed that for (arbitrarily) small  there are four other solutions to the equation (with very large magnitude). The reason we don't find these solutions in the above perturbation method is because these solutions diverge when
there are four other solutions to the equation (with very large magnitude). The reason we don't find these solutions in the above perturbation method is because these solutions diverge when  while the ansatz assumes regular behavior in this limit.
while the ansatz assumes regular behavior in this limit.
The four additional solutions can be found using the methods of singular perturbation
theory. In this case this works as follows. Since the four solutions diverge at , it makes sense to rescale
, it makes sense to rescale  . We put
. We put

such that in terms of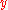 the solutions stay finite. This means that we need to choose the exponent
the solutions stay finite. This means that we need to choose the exponent  to match the rate at which the solutions diverge. In terms of
to match the rate at which the solutions diverge. In terms of 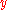 the equation reads:
the equation reads:

The 'right' value for is obtained when the exponent of
is obtained when the exponent of  in the prefactor of the term proportional to
in the prefactor of the term proportional to 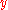 is equal to the exponent of
is equal to the exponent of  in the prefactor of the term proportional to
in the prefactor of the term proportional to  , i.e. when
, i.e. when 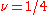 . This is called 'significant degeneration'. If we choose
. This is called 'significant degeneration'. If we choose  larger, then the four solutions will collapse to zero in terms of
larger, then the four solutions will collapse to zero in terms of 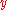 and they will become degenerate with the solution we found above. If we choose
and they will become degenerate with the solution we found above. If we choose  smaller, then the four solutions will still diverge to infinity.
smaller, then the four solutions will still diverge to infinity.
Putting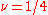 in the above equation yields:
in the above equation yields:

This equation can be solved using ordinary perturbation theory in the same way as regular expansion for was obtained. Since the expansion parameter is now
was obtained. Since the expansion parameter is now 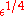 we put:
we put:

There are 5 solutions for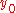 : 0, 1, -1, i and -i. We must disregard the solution
: 0, 1, -1, i and -i. We must disregard the solution  . The case
. The case  corresponds to the original regular solution which appears to be at zero for
corresponds to the original regular solution which appears to be at zero for  , because in the limit
, because in the limit  we are rescaling by an infinite amount. The next term is
we are rescaling by an infinite amount. The next term is 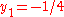 . In terms of
. In terms of  the four solutions are thus given as:
the four solutions are thus given as:

). For zero viscosity, it is not possible to impose this boundary condition and a regular perturbative expansion amounts to an expansion about an unrealistic physical solution. Singular perturbation theory can, however, be applied here and this amounts to 'zooming in' at the boundaries (using the method of matched asymptotic expansions
).
Perturbation theory can fail when the system can transition to a different "phase" of matter, with a qualitatively different behaviour, that cannot be modelled by the physical formulas put into the perturbation theory (e.g., a solid crystal melting into a liquid). In some cases, this failure manifests itself by divergent behavior of the perturbation series. Such divergent series can sometimes be resummed using techniques such as Borel resummation.
Perturbation techniques can be also used to find approximate solutions to non-linear differential equations. Examples of techniques used to find approximate solutions to these types of problems are the Lindstedt–Poincaré technique, the method of harmonic balancing, and the method of multiple time scales.
There is absolutely no guarantee that perturbative methods result in a convergent solution. In fact, asymptotic series are the norm.
use perturbation theory directly or are closely related methods. Møller–Plesset perturbation theory uses the difference between the Hartree–Fock Hamiltonian and the exact non-relativistic Hamiltonian as the perturbation. The zero-order energy is the sum of orbital energies. The first-order energy is the Hartree–Fock energy and electron correlation is included at second-order or higher. Calculations to second, third or fourth order are very common and the code is included in most ab initio quantum chemistry programs. A related but more accurate method is the coupled cluster
method.
Perturbation theory leads to an expression for the desired solution in terms of a formal power series in some "small" parameter that quantifies the deviation from the exactly solvable problem. The leading term in this power series is the solution of the exactly solvable problem, while further terms describe the deviation in the solution, due to the deviation from the initial problem. Formally, we have for the approximation to the full solution A, a series in the small parameter (here called
 ), like the following:
), like the following:
In this example,
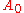 would be the known solution to the exactly solvable initial problem and
would be the known solution to the exactly solvable initial problem and 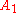 ,
,  ... represent the higher-order terms which may be found iteratively by some systematic procedure. For small
... represent the higher-order terms which may be found iteratively by some systematic procedure. For small  these higher-order terms in the series become successively smaller. An approximate "perturbation solution" is obtained by truncating the series, usually by keeping only the first two terms, the initial solution and the "first-order" perturbation correction:
these higher-order terms in the series become successively smaller. An approximate "perturbation solution" is obtained by truncating the series, usually by keeping only the first two terms, the initial solution and the "first-order" perturbation correction:
General description
Perturbation theory is closely related to methods used in numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
. The earliest use of what would now be called perturbation theory was to deal with the otherwise unsolvable mathematical problems of celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
: Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's solution for the orbit of the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, which moves noticeably differently from a simple Keplerian ellipse
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
because of the competing gravitation of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
.
Perturbation methods start with a simplified form of the original problem, which is simple enough to be solved exactly. In celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, this is usually a Keplerian ellipse
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. Under non relativistic gravity, an ellipse is exactly correct when there are only two gravitating bodies (say, the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
) but not quite correct when there are three or more objects (say, the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, and the rest of the solar system
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
).
The solved, but simplified problem is then "perturbed" to make the conditions that the perturbed solution actually satisfies closer to the real problem, such as including the gravitational attraction of a third body (the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
). The "conditions" are a formula (or several) that represent reality, often something arising from a physical law like Newton's second law, the force-acceleration equation:

In the case of the example, the force
 is calculated based on the number of gravitationally relevant bodies; the acceleration
is calculated based on the number of gravitationally relevant bodies; the acceleration  is obtained, using calculus, from the path of the Moon
is obtained, using calculus, from the path of the MoonMoon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
in its orbit. Both of these come in two forms: approximate values for force and acceleration, which result from simplifications, and hypothetical exact values for force and acceleration, which would require the complete answer to calculate.
The slight changes that result from accommodating the perturbation, which themselves may have been simplified yet again, are used as corrections to the approximate solution. Because of simplifications introduced along every step of the way, the corrections are never perfect, and the conditions met by the corrected solution do not perfectly match the equation demanded by reality, but even one cycle of corrections often provides a remarkably better approximate answer to what the real solution should be.
There is no requirement to stop at only one cycle of corrections. A partially corrected solution can be re-used as the new starting point for yet another cycle of perturbations and corrections. In principle, cycles of finding increasingly better corrections could go on indefinitely. In practice, one typically stops at one or two cycles of corrections, due to exhaustion. The usual difficulty with the method is that the corrections progressively make the new solutions very much more complicated, so each cycle is much more difficult to manage than the previous cycle of corrections. Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
is reported to have said, regarding the problem of the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
's orbit, that "It causeth my head to ache."
This general procedure is a widely used mathematical tool in advanced sciences and engineering: start with a simplified problem and gradually add corrections that make the formula that the corrected problem matches closer and closer to the formula that represents reality. It is the natural extension to mathematical functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the "guess, check, and fix" method used anciently with numbers.
Examples
Examples for the "mathematical description" are:an algebraic equation,
a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
(e.g., the equations of motion in celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
or a wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
),
a free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
(in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
),
a Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
operator (in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
).
Examples for the kind of solution to be found perturbatively:
the solution of the equation (e.g., the trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
of a particle),
the statistical average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
of some
physical quantity (e.g., average magnetization),
the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
energy of a quantum mechanical
problem.
Examples for the exactly solvable problems to start with:
linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s, including linear equations of motion
(harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
, linear wave equation), statistical or quantum-mechanical systems of
non-interacting particles (or in general, Hamiltonians or free
energies containing only terms quadratic in all degrees of freedom).
Examples of "perturbations" to deal with:
Nonlinear contributions to the equations of motion, interaction
Interaction
Interaction is a kind of action that occurs as two or more objects have an effect upon one another. The idea of a two-way effect is essential in the concept of interaction, as opposed to a one-way causal effect...
s
between particles, terms of higher powers in the Hamiltonian/Free Energy.
For physical problems involving interactions between particles,
the terms of the perturbation series may be displayed (and
manipulated) using Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s.
History
Perturbation theory has its roots in early celestial mechanicsCelestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, where the theory of epicycles was used to make small corrections to the predicted paths of planets. Curiously, it was the need for more and more epicycles that eventually led to the 16th century Copernican revolution
Copernican Revolution
The Copernican Revolution refers to the paradigm shift away from the Ptolemaic model of the heavens, which postulated the Earth at the center of the galaxy, towards the heliocentric model with the Sun at the center of our Solar System...
in the understanding of planetary orbits. The development of basic perturbation theory for differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s was fairly complete by the middle of the 19th century. It was at that time that Charles-Eugène Delaunay
Charles-Eugène Delaunay
Charles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...
was studying the perturbative expansion for the Earth-Moon-Sun system, and discovered the so-called "problem of small denominators". Here, the denominator appearing in the n
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
to make one of the first deductions of the existence of chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, or what is prosaically called the "butterfly effect
Butterfly effect
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
": that even a very small perturbation can have a very large effect on a system.
Perturbation theory saw a particularly dramatic expansion and evolution with the arrival of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Although perturbation theory was used in the semi-classical theory of the Bohr atom, the calculations were monstrously complicated, and subject to somewhat ambiguous interpretation. The discovery of Heisenberg's matrix mechanics
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
allowed a vast simplification of the application of perturbation theory. Notable examples are the Stark effect
Stark effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
and the Zeeman effect
Zeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
, which have a simple enough theory to be included in standard undergraduate textbooks in quantum mechanics. Other early applications include the fine structure
Fine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
and the hyperfine structure
Hyperfine structure
The term hyperfine structure refers to a collection of different effects leading to small shifts and splittings in the energy levels of atoms, molecules and ions. The name is a reference to the fine structure which results from the interaction between the magnetic moments associated with electron...
in the hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
.
In modern times, perturbation theory underlies much of quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. In chemistry, perturbation theory was used to obtain the first solutions for the helium atom
Helium atom
Helium is an element and the next simplest atom to solve after the hydrogen atom. Helium is composed of two electrons in orbit around a nucleus containing two protons along with either one or two neutrons, depending on the isotope. The hydrogen atom is used extensively to aid in solving the helium...
.
In the middle of the 20th century, Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
realized that the perturbative expansion could be given a dramatic and beautiful graphical representation in terms of what are now called Feynman diagrams. Although originally applied only in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, such diagrams now find increasing use in any area where perturbative expansions are studied.
A partial resolution of the small-divisor problem was given by the statement of the KAM theorem in 1954. Developed by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
and Jürgen Moser
Jürgen Moser
Jürgen Kurt Moser or Juergen Kurt Moser was a German-American mathematician.-Professional biography:...
, this theorem stated the conditions under which a system of partial differential equations will have only mildly chaotic behaviour under small perturbations.
In the late 20th century, broad dissatisfaction with perturbation theory in the quantum physics community, including not only the difficulty of going beyond second order in the expansion, but also questions about whether the perturbative expansion is even convergent, has led to a strong interest in the area of non-perturbative analysis, that is, the study of exactly solvable models. The prototypical model is the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
, a highly non-linear equation for which the interesting solutions, the soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s, cannot be reached by perturbation theory, even if the perturbations were carried out to infinite order. Much of the theoretical work in non-perturbative analysis goes under the name of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s and non-commutative geometry.
Perturbation orders
The standard exposition of perturbation theory is given in terms of the order to which the perturbation is carried out: first-order perturbation theory or second-order perturbation theory, and whether the perturbed states are degenerate (that is, singularSingular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
), in which case extra care must be taken, and the theory is slightly more difficult.
- This section needs to be expanded to include the standard textbook examples of each of the three expansions.
First-order non-singular perturbation theory
This section develops, in simplified terms, the general theory for the perturbative solution to a differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
to the first order. To keep the exposition simple, a crucial assumption is made: that the solutions to the unperturbed system are not degenerate
Degenerate form
In mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
, so that the perturbation series can be inverted. There are ways of dealing with the degenerate (or singular
Singular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
) case; these require extra care.
Suppose one wants to solve a differential equation of the form
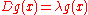
where D is some specific differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, and
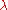 is an eigenvalue. Many problems involving ordinary or partial differential equations can be cast in this form. It is presumed that the differential operator can be written in the form
is an eigenvalue. Many problems involving ordinary or partial differential equations can be cast in this form. It is presumed that the differential operator can be written in the form
where
 is presumed to be small, and that furthermore, the complete set of solutions for
is presumed to be small, and that furthermore, the complete set of solutions for 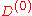 are known. That is,one has a set of solutions
are known. That is,one has a set of solutions  , labelled by some arbitrary index n, such that
, labelled by some arbitrary index n, such that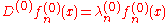 .
.Furthermore, one assumes that the set of solutions
 form an orthonormal set:
form an orthonormal set:
with
 the Kronecker delta function.
the Kronecker delta function.To zeroth order, one expects that the solutions
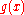 are then somehow "close" to one of the unperturbed solutions
are then somehow "close" to one of the unperturbed solutions  . That is,
. That is,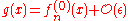
and
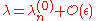 .
.where
 denotes the relative size, in big-O notation, of the perturbation. To solve this problem, one assumes that the solution
denotes the relative size, in big-O notation, of the perturbation. To solve this problem, one assumes that the solution 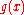 can be written as a linear combination of the
can be written as a linear combination of the  :
: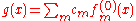
with all of the constants
 except for n, where
except for n, where  . Substituting this last expansion into the differential equation, taking the inner product of the result with
. Substituting this last expansion into the differential equation, taking the inner product of the result with 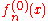 , and making use of orthogonality, one obtains
, and making use of orthogonality, one obtains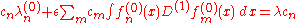
This can be trivially rewritten as a simple linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
problem of finding the eigenvalue of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, where
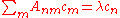
where the matrix elements
 are given by
are given by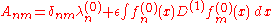
Rather than solving this full matrix equation, one notes that, of all the
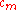 in the linear equation, only one, namely
in the linear equation, only one, namely  , is not small. Thus, to the first order in
, is not small. Thus, to the first order in  , the linear equation may be solved trivially as
, the linear equation may be solved trivially as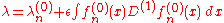
since all of the other terms in the linear equation are of order
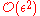 . The above gives the solution of the eigenvalue to first order in perturbation theory.
. The above gives the solution of the eigenvalue to first order in perturbation theory.The function
 to first order is obtained through similar reasoning. Substituting
to first order is obtained through similar reasoning. Substituting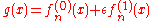
so that
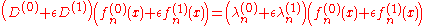
gives an equation for
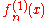 . It may be solved integrating with the partition of unity
. It may be solved integrating with the partition of unity
to give

which gives the exact solution to the perturbed differential equation to the first order in the perturbation
 .
.Several important observations can be made about the form of this solution. First, the sum over functions with differences of eigenvalues in the denominator resembles the resolvent in Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
. This is no accident; the resolvent acts essentially as a kind of Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
or propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
, passing the perturbation along. Higher-order perturbations resemble this form, with an additional sum over a resolvent appearing at each order.
The form of this solution is sufficient to illustrate the idea behind the small-divisor problem. If, for whatever reason, two eigenvalues are close so that difference
 become small, the corresponding term in the sum will become disproportionately large. In particular, if this happens in higher-order terms, the high-order perturbation may become as large or larger in magnitude than the first-order perturbation. Such a situation calls into question the validity of doing a perturbation to begin with. This can be understood to be a fairly catastrophic situation; it is frequently encountered in chaotic dynamical systems
become small, the corresponding term in the sum will become disproportionately large. In particular, if this happens in higher-order terms, the high-order perturbation may become as large or larger in magnitude than the first-order perturbation. Such a situation calls into question the validity of doing a perturbation to begin with. This can be understood to be a fairly catastrophic situation; it is frequently encountered in chaotic dynamical systemsChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, and requires the development of techniques other than perturbation theory to solve the problem.
Curiously, the situation is not at all bad if two or more eigenvalues are exactly equal. This case is referred to as singular
Singular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
or degenerate perturbation theory. The degeneracy of eigenvalues indicates that the unperturbed system has some sort of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, and that the generators of the symmetry commute with the unperturbed differential operator. Typically, the perturbing term does not possess the symmetry; one says the perturbation lifts or breaks the degeneracy. In this case, the perturbation can still be performed; however, one must be careful to work in a basis for the unperturbed states so that these map one-to-one to the perturbed states, rather than being a mixture.
Example of second-order singular perturbation theory
Consider the following equation for the unknown variable :
:
For the initial problem with
 , the solution is
, the solution is  . For small
. For small  the lowest-order approximation may be found by inserting the ansatz
the lowest-order approximation may be found by inserting the ansatzAnsatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...

into the equation and demanding the equation to be fulfilled up to terms that involve powers of
 higher than the first. This yields
higher than the first. This yields 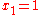 . In the same way, the higher orders may be found. However, even in this simple example it may be observed that for (arbitrarily) small
. In the same way, the higher orders may be found. However, even in this simple example it may be observed that for (arbitrarily) small  there are four other solutions to the equation (with very large magnitude). The reason we don't find these solutions in the above perturbation method is because these solutions diverge when
there are four other solutions to the equation (with very large magnitude). The reason we don't find these solutions in the above perturbation method is because these solutions diverge when  while the ansatz assumes regular behavior in this limit.
while the ansatz assumes regular behavior in this limit.The four additional solutions can be found using the methods of singular perturbation
Singular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
theory. In this case this works as follows. Since the four solutions diverge at
 , it makes sense to rescale
, it makes sense to rescale  . We put
. We put
such that in terms of
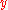 the solutions stay finite. This means that we need to choose the exponent
the solutions stay finite. This means that we need to choose the exponent  to match the rate at which the solutions diverge. In terms of
to match the rate at which the solutions diverge. In terms of 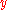 the equation reads:
the equation reads:
The 'right' value for
 is obtained when the exponent of
is obtained when the exponent of  in the prefactor of the term proportional to
in the prefactor of the term proportional to 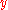 is equal to the exponent of
is equal to the exponent of  in the prefactor of the term proportional to
in the prefactor of the term proportional to  , i.e. when
, i.e. when 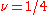 . This is called 'significant degeneration'. If we choose
. This is called 'significant degeneration'. If we choose  larger, then the four solutions will collapse to zero in terms of
larger, then the four solutions will collapse to zero in terms of 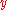 and they will become degenerate with the solution we found above. If we choose
and they will become degenerate with the solution we found above. If we choose  smaller, then the four solutions will still diverge to infinity.
smaller, then the four solutions will still diverge to infinity.Putting
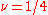 in the above equation yields:
in the above equation yields:
This equation can be solved using ordinary perturbation theory in the same way as regular expansion for
 was obtained. Since the expansion parameter is now
was obtained. Since the expansion parameter is now 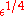 we put:
we put:
There are 5 solutions for
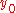 : 0, 1, -1, i and -i. We must disregard the solution
: 0, 1, -1, i and -i. We must disregard the solution  . The case
. The case  corresponds to the original regular solution which appears to be at zero for
corresponds to the original regular solution which appears to be at zero for  , because in the limit
, because in the limit  we are rescaling by an infinite amount. The next term is
we are rescaling by an infinite amount. The next term is 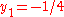 . In terms of
. In terms of  the four solutions are thus given as:
the four solutions are thus given as:
Commentary
Both regular and singular perturbation theory are frequently used in physics and engineering. Regular perturbation theory may only be used to find those solutions of a problem that evolve smoothly out of the initial solution when changing the parameter (that are "adiabatically connected" to the initial solution). A well known example from physics where regular perturbation theory fails is in fluid dynamics when one treats the viscosity as a small parameter. Close to a boundary, the fluid velocity goes to zero, even for very small viscosity (the no-slip conditionNo-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
). For zero viscosity, it is not possible to impose this boundary condition and a regular perturbative expansion amounts to an expansion about an unrealistic physical solution. Singular perturbation theory can, however, be applied here and this amounts to 'zooming in' at the boundaries (using the method of matched asymptotic expansions
Method of matched asymptotic expansions
In mathematics, particularly in solving singularly perturbed differential equations, the method of matched asymptotic expansions is a common approach to finding an accurate approximation to a problem's solution.-Method overview:...
).
Perturbation theory can fail when the system can transition to a different "phase" of matter, with a qualitatively different behaviour, that cannot be modelled by the physical formulas put into the perturbation theory (e.g., a solid crystal melting into a liquid). In some cases, this failure manifests itself by divergent behavior of the perturbation series. Such divergent series can sometimes be resummed using techniques such as Borel resummation.
Perturbation techniques can be also used to find approximate solutions to non-linear differential equations. Examples of techniques used to find approximate solutions to these types of problems are the Lindstedt–Poincaré technique, the method of harmonic balancing, and the method of multiple time scales.
There is absolutely no guarantee that perturbative methods result in a convergent solution. In fact, asymptotic series are the norm.
Perturbation theory in chemistry
Many of the ab initio quantum chemistry methodsAb initio quantum chemistry methods
Ab initio quantum chemistry methods are computational chemistry methods based on quantum chemistry. The term ab initiowas first used in quantum chemistry by Robert Parr and coworkers, including David Craig in a semiempirical study on the excited states of benzene.The background is described by Parr...
use perturbation theory directly or are closely related methods. Møller–Plesset perturbation theory uses the difference between the Hartree–Fock Hamiltonian and the exact non-relativistic Hamiltonian as the perturbation. The zero-order energy is the sum of orbital energies. The first-order energy is the Hartree–Fock energy and electron correlation is included at second-order or higher. Calculations to second, third or fourth order are very common and the code is included in most ab initio quantum chemistry programs. A related but more accurate method is the coupled cluster
Coupled cluster
Coupled cluster is a numerical technique used for describing many-body systems. Its most common use is as one of several quantum chemical post-Hartree–Fock ab initio quantum chemistry methods in the field of computational chemistry...
method.
See also
- Orders of approximationOrders of approximationIn science, engineering, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order...
- Structural stabilityStructural stabilityIn mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
- Dynamic nuclear polarisationDynamic nuclear polarisationDynamic nuclear polarization results from transferring spin polarization from electrons to nuclei, thereby aligning the nuclear spins to the extent that electron spins are aligned. Note that the alignment of electron spins at a given magnetic field and temperature is described by the Boltzmann...
- Eigenvalue perturbationEigenvalue perturbationIn mathematics, eigenvalue perturbation is a perturbation approach to finding eigenvalues and eigenvectors of systems perturbed from one with known eigenvectors and eigenvalues. It also allows one to determine the sensitivity of the eigenvalues and eigenvectors with respect to changes in the system...
- Cosmological perturbation theoryCosmological perturbation theoryIn physical cosmology, cosmological perturbation theory is the theory by which the evolution of structure is understood in the big bang model. It uses general relativity to compute the gravitational forces causing small perturbations to grow and eventually seed the formation of stars, quasars,...
- Interval FEM
External links
- Introduction to regular perturbation theory by Eric Vanden-Eijnden (PDF)
- Duality in Perturbation Theory
- Perturbation Method of Multiple Scales

