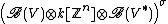Quantum group
Encyclopedia
In mathematics
and theoretical physics
, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra
. There is no single, all-encompassing definition, but instead a family of broadly similar objects.
The term "quantum group" often denotes a kind of noncommutative algebra with additional structure that first appeared in the theory of quantum integrable systems, and which was then formalized by Vladimir Drinfel'd
and Michio Jimbo
as a particular class of Hopf algebra
. The same term is also used for other Hopf algebras that deform or are close to classical Lie groups or Lie algebras, such as a `bicrossproduct' class of quantum groups introduced by Shahn Majid a little after the work of Drinfeld and Jimbo.
In Drinfeld's approach, quantum groups arise as Hopf algebra
s depending on an auxiliary parameter q or h, which become universal enveloping algebra
s of a certain Lie algebra, frequently semisimple or affine
, when q = 1 or h = 0. Closely related are certain dual objects, also Hopf algebras and also called quantum groups, deforming the algebra of functions on the corresponding semisimple algebraic group
or a compact Lie group.
Just as groups often appear as symmetries, quantum groups act on many other mathematical objects and it has become fashionable to introduce the adjective quantum in such cases; for example there are quantum planes and quantum Grassmannians.
s that are not required to be either commutative or cocommutative. One can think of the deformed object as an algebra of functions on a "noncommutative space", in the spirit of the noncommutative geometry
of Alain Connes
. This intuition, however, came after particular classes of quantum groups had already proved their usefulness in the study of the quantum Yang-Baxter equation
and quantum inverse scattering method
developed by the Leningrad School (Ludwig Faddeev, Leon Takhtajan, Evgenii Sklyanin, Nicolai Reshetikhin
and Korepin
) and related work by the Japanese School. The intuition behind the second, bicrossproduct, class of quantum groups was different and came from the search for self-dual objects as an approach to quantum gravity
.
of a semisimple Lie algebra or, more generally, a Kac-Moody algebra, in the category of Hopf algebra
s. The resulting algebra has additional structure, making it into a quasitriangular Hopf algebra.
Let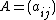 be the Cartan matrix
be the Cartan matrix
of the Kac-Moody algebra, and let q be a nonzero complex number distinct from 1, then the quantum group,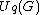 , where G is the Lie algebra whose Cartan matrix is A, is defined as the unital associative algebra
, where G is the Lie algebra whose Cartan matrix is A, is defined as the unital associative algebra
with generators (where
(where  is an element of the weight lattice, i.e.
is an element of the weight lattice, i.e. 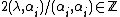 for all i), and
for all i), and 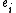 and
and 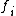 (for simple root
(for simple root
s,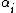 ), subject to the following relations:
), subject to the following relations:
where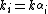 ,
, 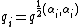 ,
, 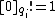 ,
, 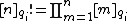 for all positive integers
for all positive integers  , and
, and 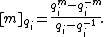 These are the q-factorial and q-number, respectively, the q-analog
These are the q-factorial and q-number, respectively, the q-analog
s of the ordinary factorial
. The last two relations above are the q-Serre relations, the deformations of the Serre
relations.
In the limit as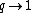 , these relations approach the relations for the universal enveloping algebra
, these relations approach the relations for the universal enveloping algebra 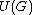 , where
, where 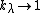 and
and  as
as  , where the element,
, where the element, 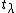 , of the Cartan subalgebra satisfies
, of the Cartan subalgebra satisfies 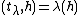 for all h in the Cartan subalgebra.
for all h in the Cartan subalgebra.
There are various coassociative coproducts
under which these algebras are Hopf algebras, for example,
In addition, any Hopf algebra leads to another with reversed coproduct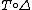 , where
, where 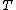 is given by
is given by 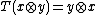 , giving three more possible versions.
, giving three more possible versions.
The counit on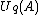 is the same for all these coproducts:
is the same for all these coproducts: 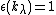 ,
, 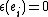 ,
, 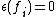 , and the respective antipodes
, and the respective antipodes
for the above coproducts are given by
Alternatively, the quantum group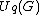 can be regarded as an algebra over the field
can be regarded as an algebra over the field 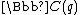 , the field of all rational function
, the field of all rational function
s of an indeterminate q over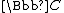 .
.
Similarly, the quantum group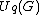 can be regarded as an algebra over the field
can be regarded as an algebra over the field 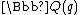 , the field of all rational function
, the field of all rational function
s of an indeterminate q over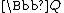 (see below in the section on quantum groups at q = 0). The center of quantum group can be described by quantum determinant.
(see below in the section on quantum groups at q = 0). The center of quantum group can be described by quantum determinant.
As is the case for all Hopf algebras,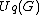 has an adjoint representation
has an adjoint representation
on itself as a module, with the action being given by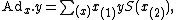 where
where 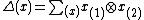 .
.
is called a weight module. A weight module is a module with a basis of weight vectors. A weight vector is a nonzero vector v such that for all
for all 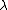 , where
, where 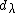 are complex numbers for all weights
are complex numbers for all weights 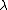 such that
such that
A weight module is called integrable if the actions of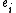 and
and 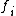 are locally nilpotent (i.e. for any vector v in the module, there exists a positive integer k, possibly dependent on v, such that
are locally nilpotent (i.e. for any vector v in the module, there exists a positive integer k, possibly dependent on v, such that 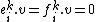 for all i). In the case of integrable modules, the complex numbers
for all i). In the case of integrable modules, the complex numbers 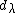 associated with a weight vector satisfy
associated with a weight vector satisfy  , where
, where  is an element of the weight lattice, and
is an element of the weight lattice, and 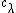 are complex numbers such that
are complex numbers such that
Of special interest are highest weight representations, and the corresponding highest weight modules. A highest weight module is a module generated by a weight vector v, subject to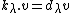 for all weights
for all weights 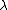 , and
, and 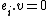 for all i. Similarly, a quantum group can have a lowest weight representation and lowest weight module, i.e. a module generated by a weight vector v, subject to
for all i. Similarly, a quantum group can have a lowest weight representation and lowest weight module, i.e. a module generated by a weight vector v, subject to 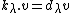 for all weights
for all weights 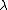 , and
, and 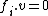 for all i.
for all i.
Define a vector v to have weight if
if 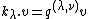 for all
for all 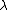 in the weight lattice.
in the weight lattice.
If G is a Kac-Moody algebra, then in any irreducible highest weight representation of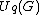 , with highest weight
, with highest weight  , the multiplicities of the weights are equal to their multiplicities in an irreducible representation of
, the multiplicities of the weights are equal to their multiplicities in an irreducible representation of 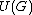 with equal highest weight. If the highest weight is dominant and integral (a weight
with equal highest weight. If the highest weight is dominant and integral (a weight  is dominant and integral if
is dominant and integral if 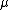 satisfies the condition that
satisfies the condition that 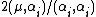 is a non-negative integer for all i), then the weight spectrum of the irreducible representation is invariant under the Weyl group
is a non-negative integer for all i), then the weight spectrum of the irreducible representation is invariant under the Weyl group
for G, and the representation is integrable.
Conversely, if a highest weight module is integrable, then its highest weight vector v satisfies , where
, where 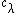 are complex numbers such that
are complex numbers such that
and is dominant and integral.
is dominant and integral.
As is the case for all Hopf algebras, the tensor product
of two modules is another module. For an element x of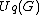 , and for vectors v and w in the respective modules,
, and for vectors v and w in the respective modules, 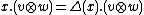 , so that
, so that 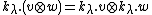 , and in the case of coproduct
, and in the case of coproduct 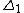 ,
, 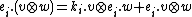 and
and 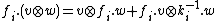 .
.
The integrable highest weight module described above is a tensor product of a one-dimensional module (on which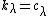 for all
for all 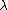 , and
, and 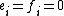 for all i) and a highest weight module generated by a nonzero vector
for all i) and a highest weight module generated by a nonzero vector 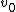 , subject to
, subject to 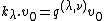 for all weights
for all weights 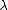 , and
, and 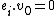 for all i.
for all i.
In the specific case where G is a finite-dimensional Lie algebra (as a special case of a Kac-Moody algebra), then the irreducible representations with dominant integral highest weights are also finite-dimensional.
In the case of a tensor product of highest weight modules, its decomposition into submodules is the same as for the tensor product of the corresponding modules of the Kac-Moody algebra (the highest weights are the same, as are their multiplicities).
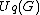 is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of an R-matrix. This infinite formal sum is expressible in terms of generators
is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of an R-matrix. This infinite formal sum is expressible in terms of generators 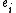 and
and 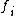 , and Cartan generators
, and Cartan generators 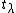 , where
, where 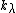 is formally identified with
is formally identified with 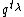 . The infinite formal sum is the product of two factors,
. The infinite formal sum is the product of two factors, 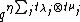 , and an infinite formal sum, where
, and an infinite formal sum, where 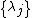 is a basis for the dual space to the Cartan subalgebra, and
is a basis for the dual space to the Cartan subalgebra, and  is the dual basis, and
is the dual basis, and  is a sign (+1 or -1).
is a sign (+1 or -1).
The formal infinite sum which plays the part of the R-matrix has a well-defined action on the tensor product of two irreducible highest weight modules, and also on the tensor product if two lowest weight modules. Specifically, if v has weight and w has weight
and w has weight 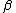 , then
, then 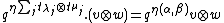 , and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor on
, and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor on 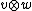 to a finite sum.
to a finite sum.
Specifically, if V is a highest weight module, then the formal infinite sum, R, has a well-defined, and invertible, action on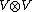 , and this value of R (as an element of
, and this value of R (as an element of 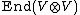 ) satisfies the Yang-Baxter equation
) satisfies the Yang-Baxter equation
, and therefore allows us to determine a representation of the braid group
, and to define quasi-invariants for knots
, links
and braids
.
has researched the limiting behaviour of quantum groups as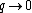 , and found a particularly well behaved base called a crystal base
, and found a particularly well behaved base called a crystal base
.
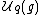 for
for 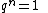 ; one usually considers the class of pointed Hopf algebras, meaning that all subcoideals are 1-dimensional and thus there sum form a group called coradical:
; one usually considers the class of pointed Hopf algebras, meaning that all subcoideals are 1-dimensional and thus there sum form a group called coradical:
This could recently be used on the specific cases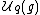 and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups to the order of the Weyl group
and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups to the order of the Weyl group
of the Lie algebra
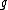 .
.
.
S.L. Woronowicz introduced compact matrix quantum groups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry
.
The continuous complex-valued functions on a compact Hausdorff topological space form a commutative C*-algebra. By the Gelfand theorem
, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism
.
For a compact topological group
, G, there exists a C*-algebra homomorphism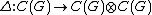 (where
(where  is the C*-algebra tensor product - the completion of the algebraic tensor product of
is the C*-algebra tensor product - the completion of the algebraic tensor product of 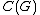 and
and 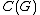 ), such that
), such that 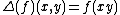 for all
for all 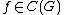 , and for all
, and for all 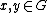 (where
(where 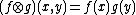 for all
for all 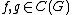 and all
and all 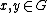 ). There also exists a linear multiplicative mapping
). There also exists a linear multiplicative mapping 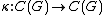 , such that
, such that 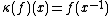 for all
for all 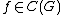 and all
and all  . Strictly, this does not make
. Strictly, this does not make 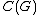 a Hopf algebra, unless G is finite. On the other hand, a finite-dimensional representation
a Hopf algebra, unless G is finite. On the other hand, a finite-dimensional representation
of G can be used to generate a *-subalgebra of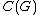 which is also a Hopf *-algebra. Specifically, if
which is also a Hopf *-algebra. Specifically, if 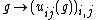 is an
is an  -dimensional representation of
-dimensional representation of 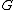 , then
, then 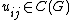 for all
for all 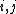 , and
, and  for all
for all  . It follows that the *-algebra generated by
. It follows that the *-algebra generated by 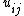 for all
for all 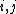 and
and  for all
for all 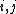 is a Hopf *-algebra: the counit is determined by
is a Hopf *-algebra: the counit is determined by 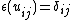 for all
for all 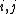 (where
(where 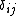 is the Kronecker delta), the antipode is
is the Kronecker delta), the antipode is  , and the unit is given by
, and the unit is given by 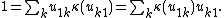
As a generalization, a compact matrix quantum group is defined as a pair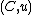 , where
, where 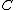 is a C*-algebra and
is a C*-algebra and  is a matrix with entries in
is a matrix with entries in 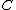 such that
such that
As a consequence of continuity, the comultiplication on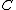 is coassociative.
is coassociative.
In general,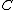 is not a bialgebra, and
is not a bialgebra, and  is a Hopf *-algebra.
is a Hopf *-algebra.
Informally,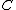 can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and
can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and  can be regarded as a finite-dimensional representation of the compact matrix quantum group.
can be regarded as a finite-dimensional representation of the compact matrix quantum group.
A representation of the compact matrix quantum group is given by a corepresentation
of the Hopf *-algebra (a corepresentation of a counital coassociative coalgebra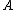 is a square matrix
is a square matrix 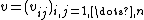 with entries in
with entries in 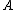 (so
(so 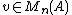 ) such that
) such that 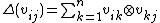 for all
for all 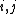 and
and 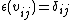 for all
for all 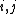 ). Furthermore, a representation v, is called unitary if the matrix for v is unitary (or equivalently, if
). Furthermore, a representation v, is called unitary if the matrix for v is unitary (or equivalently, if 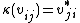 for all i, j).
for all i, j).
An example of a compact matrix quantum group is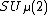 , where the parameter
, where the parameter 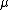 is a positive real number. So
is a positive real number. So 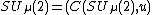 , where
, where 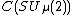 is the C*-algebra generated by
is the C*-algebra generated by  and
and 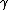 ,subject to
,subject to
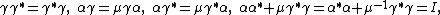
and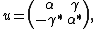 so that the comultiplication is determined by
so that the comultiplication is determined by 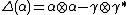 ,
, 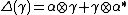 , and the coinverse is determined by
, and the coinverse is determined by  ,
,  ,
, 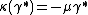 ,
, 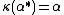 . Note that
. Note that  is a representation, but not a unitary representation.
is a representation, but not a unitary representation.  is equivalent to the unitary representation
is equivalent to the unitary representation 
Equivalently, , where
, where 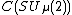 is the C*-algebra generated by
is the C*-algebra generated by  and
and 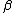 ,subject to
,subject to
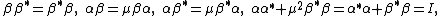
and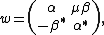 so that the comultiplication is determined by
so that the comultiplication is determined by  ,
,  , and the coinverse is determined by
, and the coinverse is determined by 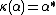 ,
, 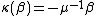 ,
, 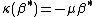 ,
, 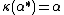 . Note that
. Note that 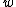 is a unitary representation. The realizations can be identified by equating
is a unitary representation. The realizations can be identified by equating 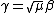 .
.
When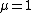 , then
, then 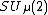 is equal to the algebra
is equal to the algebra  of functions on the concrete compact group
of functions on the concrete compact group 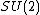 .
.
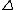 with the second factor acting back on the first. The very simplest nontrivial example corresponds to two copies of
with the second factor acting back on the first. The very simplest nontrivial example corresponds to two copies of 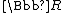 locally acting on each other and results in a quantum group (given here in an algebraic form) with generators
locally acting on each other and results in a quantum group (given here in an algebraic form) with generators 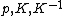 , say, and coproduct
, say, and coproduct
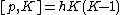 ,
, 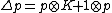 ,
, 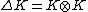
where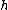 is the deformation parameter. This quantum group was linked to a toy model of Planck scale physics implementing Born reciprocity when viewed as a deformation of the Heisenberg algebra of quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebra
is the deformation parameter. This quantum group was linked to a toy model of Planck scale physics implementing Born reciprocity when viewed as a deformation of the Heisenberg algebra of quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebra 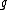 its complexification as a real Lie algebra of twice the dimension splits into
its complexification as a real Lie algebra of twice the dimension splits into 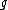 and a certain solvable Lie algebra (the Iwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated to
and a certain solvable Lie algebra (the Iwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated to  . For
. For 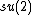 one obtains a quantum group deformation of the Euclidean group
one obtains a quantum group deformation of the Euclidean group
E(3) of motions in 3 dimensions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
. There is no single, all-encompassing definition, but instead a family of broadly similar objects.
The term "quantum group" often denotes a kind of noncommutative algebra with additional structure that first appeared in the theory of quantum integrable systems, and which was then formalized by Vladimir Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
and Michio Jimbo
Michio Jimbo
is a Japanese mathematician, currently a professor at the University of Tokyo. He is a grandson of the linguist Kaku Jimbo.After graduating from the University of Tokyo in 1974, he studied under Mikio Sato at the Research Institute for Mathematical Sciences in Kyoto University...
as a particular class of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
. The same term is also used for other Hopf algebras that deform or are close to classical Lie groups or Lie algebras, such as a `bicrossproduct' class of quantum groups introduced by Shahn Majid a little after the work of Drinfeld and Jimbo.
In Drinfeld's approach, quantum groups arise as Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s depending on an auxiliary parameter q or h, which become universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
s of a certain Lie algebra, frequently semisimple or affine
Affine Lie algebra
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
, when q = 1 or h = 0. Closely related are certain dual objects, also Hopf algebras and also called quantum groups, deforming the algebra of functions on the corresponding semisimple algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
or a compact Lie group.
Just as groups often appear as symmetries, quantum groups act on many other mathematical objects and it has become fashionable to introduce the adjective quantum in such cases; for example there are quantum planes and quantum Grassmannians.
Intuitive meaning
The discovery of quantum groups was quite unexpected, since it was known for a long time that compact groups and semisimple Lie algebras are "rigid" objects, in other words, they cannot be "deformed". One of the ideas behind quantum groups is that if we consider a structure that is in a sense equivalent but larger, namely a group algebra or a universal enveloping algebra, then a group or enveloping algebra can be "deformed", although the deformation will no longer remain a group or enveloping algebra. More precisely, deformation can be accomplished within the category of Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s that are not required to be either commutative or cocommutative. One can think of the deformed object as an algebra of functions on a "noncommutative space", in the spirit of the noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
of Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
. This intuition, however, came after particular classes of quantum groups had already proved their usefulness in the study of the quantum Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
and quantum inverse scattering method
Quantum inverse scattering method
Quantum inverse scattering method relates two different approaches:1) Inverse scattering transform is a method of solving classical integrable differential equations of evolutionary type.Important concept is Lax representation....
developed by the Leningrad School (Ludwig Faddeev, Leon Takhtajan, Evgenii Sklyanin, Nicolai Reshetikhin
Nicolai Reshetikhin
Nicolai Yuryevich Reshetikhin is a mathematical physicist, currently a professor of mathematics at the University of California, Berkeley and a professor of mathematical physics at the University of Amsterdam. His research is in the fields of low-dimensional topology, representation theory, and...
and Korepin
Vladimir Korepin
Vladimir Korepin is a Russian-American physicist and mathematician. He is a professor at the C. N. Yang Institute of Theoretical Physics of the State University of New York at Stony Brook...
) and related work by the Japanese School. The intuition behind the second, bicrossproduct, class of quantum groups was different and came from the search for self-dual objects as an approach to quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
.
Drinfel'd-Jimbo type quantum groups
One type of objects commonly called a "quantum group" appeared in the work of Vladimir Drinfel'd and Michio Jimbo as a deformation of the universal enveloping algebraUniversal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a semisimple Lie algebra or, more generally, a Kac-Moody algebra, in the category of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s. The resulting algebra has additional structure, making it into a quasitriangular Hopf algebra.
Let
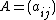 be the Cartan matrix
be the Cartan matrixCartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
of the Kac-Moody algebra, and let q be a nonzero complex number distinct from 1, then the quantum group,
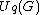 , where G is the Lie algebra whose Cartan matrix is A, is defined as the unital associative algebra
, where G is the Lie algebra whose Cartan matrix is A, is defined as the unital associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
with generators
 (where
(where  is an element of the weight lattice, i.e.
is an element of the weight lattice, i.e. 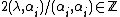 for all i), and
for all i), and 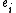 and
and 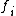 (for simple root
(for simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s,
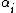 ), subject to the following relations:
), subject to the following relations: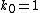 ,
,
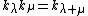 ,
,
 ,
,
 ,
,
 ,
,
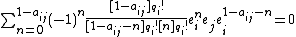 , for
, for  ,
,
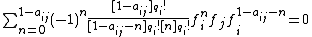 , for
, for  ,
,
where
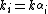 ,
, 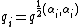 ,
, 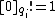 ,
, 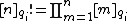 for all positive integers
for all positive integers  , and
, and 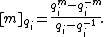 These are the q-factorial and q-number, respectively, the q-analog
These are the q-factorial and q-number, respectively, the q-analogQ-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
s of the ordinary factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
. The last two relations above are the q-Serre relations, the deformations of the Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
relations.
In the limit as
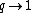 , these relations approach the relations for the universal enveloping algebra
, these relations approach the relations for the universal enveloping algebra 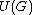 , where
, where 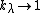 and
and  as
as  , where the element,
, where the element, 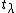 , of the Cartan subalgebra satisfies
, of the Cartan subalgebra satisfies 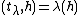 for all h in the Cartan subalgebra.
for all h in the Cartan subalgebra.There are various coassociative coproducts
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
under which these algebras are Hopf algebras, for example,
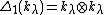 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
, 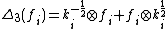 , where the set of generators has been extended, if required, to include
, where the set of generators has been extended, if required, to include  for λ which is expressible as the sum of an element of the weight lattice and half an element of the root lattice.
for λ which is expressible as the sum of an element of the weight lattice and half an element of the root lattice.
In addition, any Hopf algebra leads to another with reversed coproduct
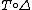 , where
, where 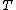 is given by
is given by 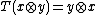 , giving three more possible versions.
, giving three more possible versions.The counit on
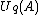 is the same for all these coproducts:
is the same for all these coproducts: 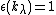 ,
, 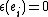 ,
, 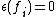 , and the respective antipodes
, and the respective antipodesHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
for the above coproducts are given by
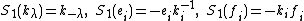 ,
,
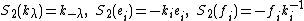 ,
,
Alternatively, the quantum group
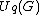 can be regarded as an algebra over the field
can be regarded as an algebra over the field 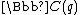 , the field of all rational function
, the field of all rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s of an indeterminate q over
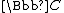 .
.Similarly, the quantum group
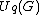 can be regarded as an algebra over the field
can be regarded as an algebra over the field 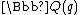 , the field of all rational function
, the field of all rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s of an indeterminate q over
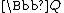 (see below in the section on quantum groups at q = 0). The center of quantum group can be described by quantum determinant.
(see below in the section on quantum groups at q = 0). The center of quantum group can be described by quantum determinant.Representation theory
Just as there are many different types of representations for Kac-Moody algebras and their universal enveloping algebras, so there are many different types of representation for quantum groups.As is the case for all Hopf algebras,
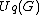 has an adjoint representation
has an adjoint representationAdjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
on itself as a module, with the action being given by
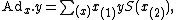 where
where 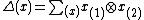 .
.Case 1: q is not a root of unity
One important type of representation is a weight representation, and the corresponding moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
is called a weight module. A weight module is a module with a basis of weight vectors. A weight vector is a nonzero vector v such that
 for all
for all 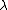 , where
, where 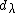 are complex numbers for all weights
are complex numbers for all weights 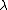 such that
such that ,
,
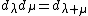 , for all weights
, for all weights  and
and  .
.
A weight module is called integrable if the actions of
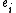 and
and 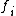 are locally nilpotent (i.e. for any vector v in the module, there exists a positive integer k, possibly dependent on v, such that
are locally nilpotent (i.e. for any vector v in the module, there exists a positive integer k, possibly dependent on v, such that 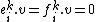 for all i). In the case of integrable modules, the complex numbers
for all i). In the case of integrable modules, the complex numbers 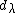 associated with a weight vector satisfy
associated with a weight vector satisfy  , where
, where  is an element of the weight lattice, and
is an element of the weight lattice, and 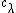 are complex numbers such that
are complex numbers such that , for all weights
, for all weights  and
and  ,
,
 for all i.
for all i.
Of special interest are highest weight representations, and the corresponding highest weight modules. A highest weight module is a module generated by a weight vector v, subject to
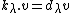 for all weights
for all weights 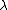 , and
, and 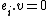 for all i. Similarly, a quantum group can have a lowest weight representation and lowest weight module, i.e. a module generated by a weight vector v, subject to
for all i. Similarly, a quantum group can have a lowest weight representation and lowest weight module, i.e. a module generated by a weight vector v, subject to 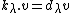 for all weights
for all weights 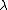 , and
, and 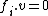 for all i.
for all i.Define a vector v to have weight
 if
if 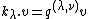 for all
for all 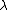 in the weight lattice.
in the weight lattice.If G is a Kac-Moody algebra, then in any irreducible highest weight representation of
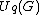 , with highest weight
, with highest weight  , the multiplicities of the weights are equal to their multiplicities in an irreducible representation of
, the multiplicities of the weights are equal to their multiplicities in an irreducible representation of 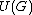 with equal highest weight. If the highest weight is dominant and integral (a weight
with equal highest weight. If the highest weight is dominant and integral (a weight  is dominant and integral if
is dominant and integral if 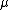 satisfies the condition that
satisfies the condition that 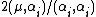 is a non-negative integer for all i), then the weight spectrum of the irreducible representation is invariant under the Weyl group
is a non-negative integer for all i), then the weight spectrum of the irreducible representation is invariant under the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
for G, and the representation is integrable.
Conversely, if a highest weight module is integrable, then its highest weight vector v satisfies
 , where
, where 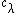 are complex numbers such that
are complex numbers such that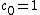 ,
,
 , for all weights
, for all weights 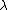 and
and  ,
,
 for all i,
for all i,
and
 is dominant and integral.
is dominant and integral.As is the case for all Hopf algebras, the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of two modules is another module. For an element x of
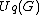 , and for vectors v and w in the respective modules,
, and for vectors v and w in the respective modules, 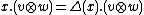 , so that
, so that 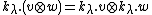 , and in the case of coproduct
, and in the case of coproduct 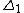 ,
, 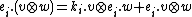 and
and 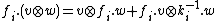 .
.The integrable highest weight module described above is a tensor product of a one-dimensional module (on which
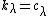 for all
for all 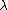 , and
, and 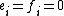 for all i) and a highest weight module generated by a nonzero vector
for all i) and a highest weight module generated by a nonzero vector 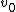 , subject to
, subject to 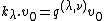 for all weights
for all weights 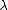 , and
, and 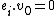 for all i.
for all i.In the specific case where G is a finite-dimensional Lie algebra (as a special case of a Kac-Moody algebra), then the irreducible representations with dominant integral highest weights are also finite-dimensional.
In the case of a tensor product of highest weight modules, its decomposition into submodules is the same as for the tensor product of the corresponding modules of the Kac-Moody algebra (the highest weights are the same, as are their multiplicities).
Case 1: q is not a root of unity
Strictly, the quantum group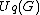 is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of an R-matrix. This infinite formal sum is expressible in terms of generators
is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of an R-matrix. This infinite formal sum is expressible in terms of generators 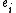 and
and 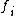 , and Cartan generators
, and Cartan generators 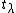 , where
, where 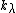 is formally identified with
is formally identified with 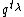 . The infinite formal sum is the product of two factors,
. The infinite formal sum is the product of two factors, 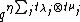 , and an infinite formal sum, where
, and an infinite formal sum, where 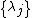 is a basis for the dual space to the Cartan subalgebra, and
is a basis for the dual space to the Cartan subalgebra, and  is the dual basis, and
is the dual basis, and  is a sign (+1 or -1).
is a sign (+1 or -1).The formal infinite sum which plays the part of the R-matrix has a well-defined action on the tensor product of two irreducible highest weight modules, and also on the tensor product if two lowest weight modules. Specifically, if v has weight
 and w has weight
and w has weight 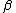 , then
, then 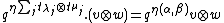 , and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor on
, and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor on 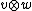 to a finite sum.
to a finite sum.Specifically, if V is a highest weight module, then the formal infinite sum, R, has a well-defined, and invertible, action on
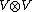 , and this value of R (as an element of
, and this value of R (as an element of 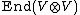 ) satisfies the Yang-Baxter equation
) satisfies the Yang-Baxter equationYang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
, and therefore allows us to determine a representation of the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
, and to define quasi-invariants for knots
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
, links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
and braids
Braid theory
In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...
.
Quantum groups at q = 0
Masaki KashiwaraMasaki Kashiwara
is a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
has researched the limiting behaviour of quantum groups as
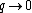 , and found a particularly well behaved base called a crystal base
, and found a particularly well behaved base called a crystal baseCrystal base
In algebra, a crystal base or canonical base is a base of a representation, such that generators of a quantum group or semisimple Lie algebra have a particularly simple action on it...
.
Description and classification by root-systems and Dynkin diagrams
There has been considerable progress in describing finite quotients of quantum groups such as the above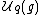 for
for 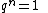 ; one usually considers the class of pointed Hopf algebras, meaning that all subcoideals are 1-dimensional and thus there sum form a group called coradical:
; one usually considers the class of pointed Hopf algebras, meaning that all subcoideals are 1-dimensional and thus there sum form a group called coradical:
- In 2002 H.-J. Schneider and N. Andruskiewitsch finished their long-term classification effort of pointed Hopf algebras with coradical an abelian group (excluding primes 2, 3, 5, 7), especially as the above finite quotients of
 Just like ordinary Semisimple Lie algebra they decompose into E´s (Borel part), dual F´s and K´s (Cartan algebra):
Just like ordinary Semisimple Lie algebra they decompose into E´s (Borel part), dual F´s and K´s (Cartan algebra):
-
- Here, as in the classical theory V is a braided vector spaceBraided vector spaceIn mathematics, a braided vectorspace \;V is a vectorspace together with an additional structure map \tau\; symbolizing interchanging of two vector tensor copies:such that the Yang–Baxter equation is fulfilled...
of dimension n spanned by the E´s, and (a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. The role of the quantum Borel algebra is taken by a Nichols algebra
(a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. The role of the quantum Borel algebra is taken by a Nichols algebra 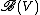 of the braided vectorspace.
of the braided vectorspace.
- A crucial ingredience was hence the classification of finite Nichols algebras for abelian groups by I. Heckenberger in terms of generalized Dynkin diagrams. When small primes are present, some exotic examples, such as a trianle, occur:
- Here, as in the classical theory V is a braided vector space
- In the meanwhile, Schneider and Heckenbergen have generally proven the existance of an arithmetic root systemRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
also in then nonabelian case, generating a PBW basis as proven by Kharcheko in the abelian case (without the assumption on finite dimension).
This could recently be used on the specific cases
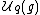 and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups to the order of the Weyl group
and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups to the order of the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
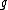 .
.Compact matrix quantum groups
See also compact quantum groupCompact quantum group
In mathematics, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group....
.
S.L. Woronowicz introduced compact matrix quantum groups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
.
The continuous complex-valued functions on a compact Hausdorff topological space form a commutative C*-algebra. By the Gelfand theorem
Gelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
For a compact topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, G, there exists a C*-algebra homomorphism
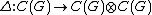 (where
(where  is the C*-algebra tensor product - the completion of the algebraic tensor product of
is the C*-algebra tensor product - the completion of the algebraic tensor product of 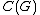 and
and 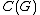 ), such that
), such that 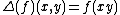 for all
for all 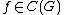 , and for all
, and for all 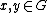 (where
(where 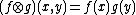 for all
for all 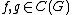 and all
and all 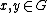 ). There also exists a linear multiplicative mapping
). There also exists a linear multiplicative mapping 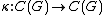 , such that
, such that 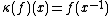 for all
for all 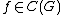 and all
and all  . Strictly, this does not make
. Strictly, this does not make 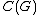 a Hopf algebra, unless G is finite. On the other hand, a finite-dimensional representation
a Hopf algebra, unless G is finite. On the other hand, a finite-dimensional representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G can be used to generate a *-subalgebra of
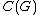 which is also a Hopf *-algebra. Specifically, if
which is also a Hopf *-algebra. Specifically, if 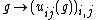 is an
is an  -dimensional representation of
-dimensional representation of 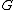 , then
, then 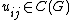 for all
for all 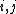 , and
, and  for all
for all  . It follows that the *-algebra generated by
. It follows that the *-algebra generated by 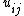 for all
for all 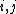 and
and  for all
for all 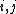 is a Hopf *-algebra: the counit is determined by
is a Hopf *-algebra: the counit is determined by 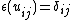 for all
for all 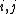 (where
(where 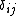 is the Kronecker delta), the antipode is
is the Kronecker delta), the antipode is  , and the unit is given by
, and the unit is given by 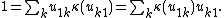
As a generalization, a compact matrix quantum group is defined as a pair
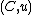 , where
, where 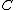 is a C*-algebra and
is a C*-algebra and  is a matrix with entries in
is a matrix with entries in 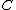 such that
such that- The *-subalgebra,
 , of
, of  , which is generated by the matrix elements of
, which is generated by the matrix elements of  , is dense in
, is dense in 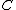 ;
;
- There exists a C*-algebra homomorphism
 (where
(where  is the C*-algebra tensor product - the completion of the algebraic tensor product of
is the C*-algebra tensor product - the completion of the algebraic tensor product of  and
and  ) such that
) such that  for all
for all  (
( is called the comultiplication);
is called the comultiplication);
- There exists a linear antimultiplicative map
 (the coinverse) such that
(the coinverse) such that 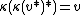 for all
for all 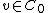 and
and  where
where 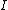 is the identity element of
is the identity element of 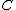 . Since
. Since  is antimultiplicative, then
is antimultiplicative, then 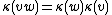 for all
for all  .
.
As a consequence of continuity, the comultiplication on
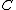 is coassociative.
is coassociative.In general,
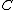 is not a bialgebra, and
is not a bialgebra, and  is a Hopf *-algebra.
is a Hopf *-algebra.Informally,
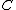 can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and
can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and  can be regarded as a finite-dimensional representation of the compact matrix quantum group.
can be regarded as a finite-dimensional representation of the compact matrix quantum group.A representation of the compact matrix quantum group is given by a corepresentation
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
of the Hopf *-algebra (a corepresentation of a counital coassociative coalgebra
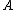 is a square matrix
is a square matrix 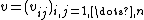 with entries in
with entries in 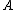 (so
(so 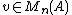 ) such that
) such that 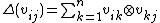 for all
for all 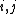 and
and 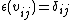 for all
for all 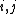 ). Furthermore, a representation v, is called unitary if the matrix for v is unitary (or equivalently, if
). Furthermore, a representation v, is called unitary if the matrix for v is unitary (or equivalently, if 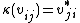 for all i, j).
for all i, j).An example of a compact matrix quantum group is
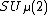 , where the parameter
, where the parameter 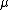 is a positive real number. So
is a positive real number. So 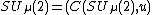 , where
, where 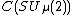 is the C*-algebra generated by
is the C*-algebra generated by  and
and 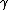 ,subject to
,subject to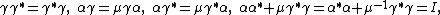
and
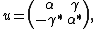 so that the comultiplication is determined by
so that the comultiplication is determined by 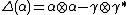 ,
, 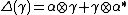 , and the coinverse is determined by
, and the coinverse is determined by  ,
,  ,
, 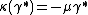 ,
, 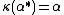 . Note that
. Note that  is a representation, but not a unitary representation.
is a representation, but not a unitary representation.  is equivalent to the unitary representation
is equivalent to the unitary representation 
Equivalently,
 , where
, where 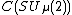 is the C*-algebra generated by
is the C*-algebra generated by  and
and 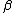 ,subject to
,subject to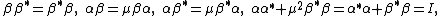
and
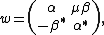 so that the comultiplication is determined by
so that the comultiplication is determined by  ,
,  , and the coinverse is determined by
, and the coinverse is determined by 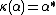 ,
, 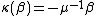 ,
, 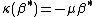 ,
, 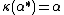 . Note that
. Note that 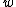 is a unitary representation. The realizations can be identified by equating
is a unitary representation. The realizations can be identified by equating 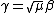 .
.When
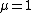 , then
, then 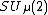 is equal to the algebra
is equal to the algebra  of functions on the concrete compact group
of functions on the concrete compact group 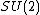 .
.Bicrossproduct quantum groups
Whereas compact matrix pseudogroups are typically versions of Drinfeld-Jimbo quantum groups in a dual function algebra formulation, with additional structure, the bicrossproduct ones are a distinct second family of quantum groups of increasing importance as deformations of solvable rather than semisimple Lie groups. They are associated to Lie splittings of Lie algebras or local factorisations of Lie groups and can be viewed as the cross product or Mackey quantisation of one of the factors acting on the other for the algebra and a similar story for the coproduct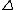 with the second factor acting back on the first. The very simplest nontrivial example corresponds to two copies of
with the second factor acting back on the first. The very simplest nontrivial example corresponds to two copies of 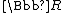 locally acting on each other and results in a quantum group (given here in an algebraic form) with generators
locally acting on each other and results in a quantum group (given here in an algebraic form) with generators 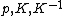 , say, and coproduct
, say, and coproduct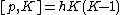 ,
, 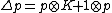 ,
, 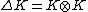
where
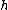 is the deformation parameter. This quantum group was linked to a toy model of Planck scale physics implementing Born reciprocity when viewed as a deformation of the Heisenberg algebra of quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebra
is the deformation parameter. This quantum group was linked to a toy model of Planck scale physics implementing Born reciprocity when viewed as a deformation of the Heisenberg algebra of quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebra 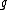 its complexification as a real Lie algebra of twice the dimension splits into
its complexification as a real Lie algebra of twice the dimension splits into 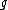 and a certain solvable Lie algebra (the Iwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated to
and a certain solvable Lie algebra (the Iwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated to  . For
. For 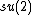 one obtains a quantum group deformation of the Euclidean group
one obtains a quantum group deformation of the Euclidean groupEuclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
E(3) of motions in 3 dimensions.
See also
- Lie bialgebraLie bialgebraIn mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: its a set with a Lie algebra and a Lie coalgebra structure which are compatible....
- Poisson–Lie group
- Affine quantum group
- Quantum affine algebras