Convergent series
Encyclopedia
In mathematics
, a series is the sum
of the terms of a sequence
of numbers.
Given a sequence
, the nth partial sum 
is the sum of the first n terms of the sequence, that is,
A series
is convergent
if the sequence of its partial sums
converges. In more formal language, a series converges if there exists a limit
such that for any arbitrarily small positive number 
, there is a large integer
such that for all 
,
A series that is not convergent is said to be divergent
.
.
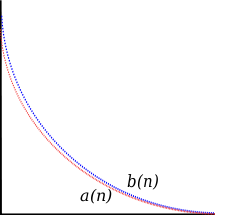Comparison test
. The terms of the sequence
are compared to those of another sequence 
. If,
for all n,
, and 
converges, then so does 
However, if,
for all n,
, and 
diverges, then so does 
Ratio test. Assume that for all n,
. Suppose that there exists 
such that
If r < 1, then the series converges. If then the series diverges. If the ratio test is inconclusive, and the series may converge or diverge.
Root test or nth root test. Suppose that the terms of the sequence in question are non-negative. Define r as follows:
If r < 1, then the series converges. If then the series diverges. If the root test is inconclusive, and the series may converge or diverge.
The ratio test and the root test are both based on comparison with a geometric series, and as such they work in similar situations. In fact, if the ratio test works (meaning that the limit exists and is not equal to 1) then so does the root test; the converse, however, is not true. The root test is therefore more generally applicable, but as a practical matter the limit is often difficult to compute for commonly seen types of series.
Integral test
. The series can be compared to an integral to establish convergence or divergence. Let
be a positive and monotone decreasing function
. If
then the series converges. But if the integral diverges, then the series does so as well.
Limit comparison test
. If
, and the limit 
exists and is not zero, then 
converges if and only if
converges.
Alternating series test
. Also known as the Leibniz criterion, the alternating series test
states that for an alternating series of the form
, if 
is monotone decreasing, and has a limit of 0 at infinity, then the series converges.
Cauchy condensation test. If
is a monotone decreasing sequence, then
converges if and only if 
converges.
Dirichlet's test
Abel's test
Raabe's test
For any sequence 
, 
for all n. Therefore,
This means that if
converges, then 
also converges (but not vice-versa).
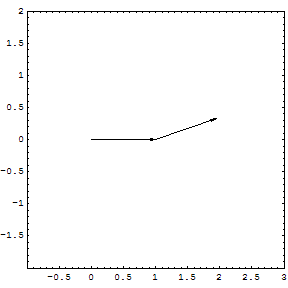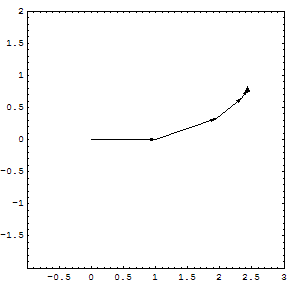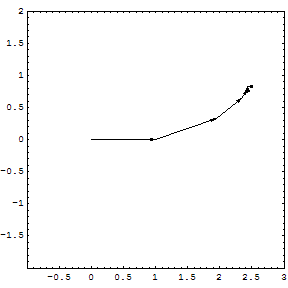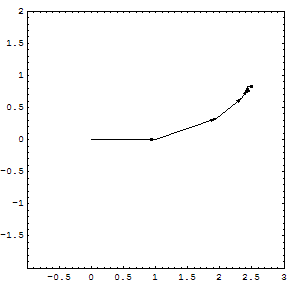
If the series
converges, then the series 
is absolutely convergent. An absolutely convergent sequence is one in which the length of the line created by joining together all of the increments to the partial sum is finitely long. The power series of the exponential function
is absolutely convergent everywhere.
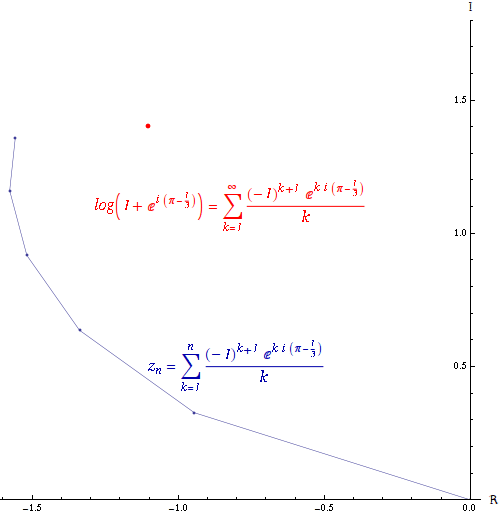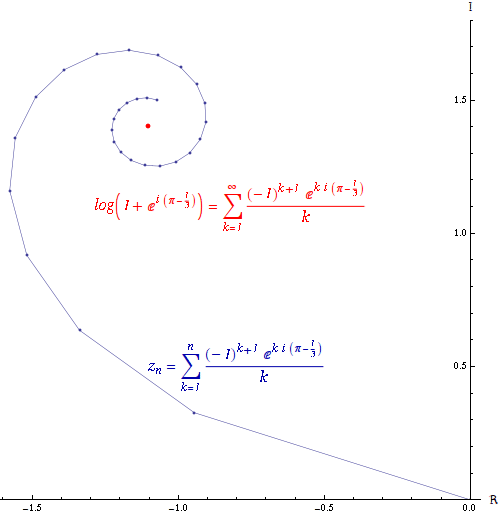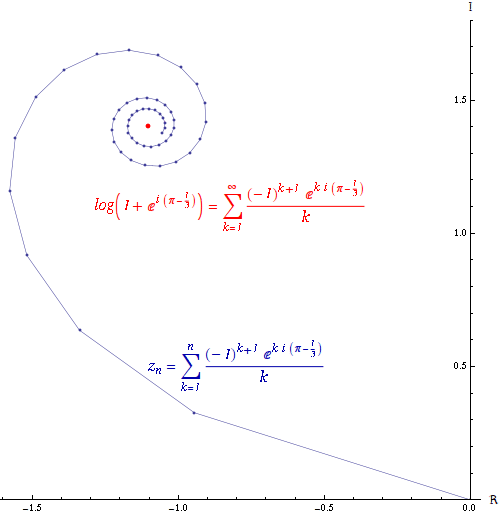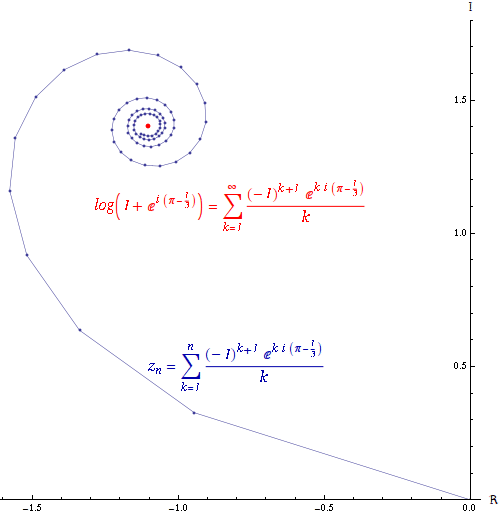
If the series
converges but the series 
diverges, then the series 
is conditionally convergent. The path formed by connecting the partial sums of a conditionally convergent series is infinitely long. The power series of the logarithm
is conditionally convergent.
The Riemann series theorem states that if a series converges conditionally, it is possible to rearrange the terms of the series in such a way that the series converges to any value, or even diverges.
Let
be a sequence of functions.
The series
is said to converge uniformly to f
if the sequence
of partial sums defined by
converges uniformly to f.
There is an analogue of the comparison test for infinite series of functions called the Weierstrass M-test.
converges if and only if
the sequence of partial sums is a Cauchy sequence
.
This means that for every
there is a positive integer 
such that for all 
we have
which is equivalent to
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a series is the sum
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
of the terms of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of numbers.
Given a sequence
, the nth partial sum is the sum of the first n terms of the sequence, that is,A series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
is convergent
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
if the sequence of its partial sums
converges. In more formal language, a series converges if there exists a limitLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
such that for any arbitrarily small positive number , there is a large integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
such that for all ,A series that is not convergent is said to be divergent
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
.
Examples of convergent and divergent series
- The reciprocals of the positive integersNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
produce a divergent seriesDivergent seriesIn mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
(harmonic seriesHarmonic series (mathematics)In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
): -
- Alternating the signs of the reciprocals of positive odd integers produces a convergent series (the Leibniz formula for pi):
-
- The reciprocals of prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s produce a divergent series (so the set of primes is "large"): -
- The reciprocals of triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s produce a convergent series: -
- The reciprocals of factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s produce a convergent series (see eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
): -
- The reciprocals of square numberSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
s produce a convergent series (the Basel problemBasel problemThe Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
): -
- The reciprocals of powers of 2Power of twoIn mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
produce a convergent series (so the set of powers of 2 is "small"): -
- Alternating the signs of reciprocals of powers of 2Power of twoIn mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
also produce a convergent series: -
- The reciprocals of Fibonacci numberFibonacci numberIn mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s produce a convergent series (see ψ): -
Convergence tests
There are a number of methods of determining whether a series converges or divergesDivergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
.
Comparison test
In mathematics, the comparison test, sometimes called the direct comparison test or CQT is a criterion for convergence or divergence of a series whose terms are real or complex numbers...
. The terms of the sequence
are compared to those of another sequence . If,for all n,
, and converges, then so does However, if,
for all n,
, and diverges, then so does Ratio test. Assume that for all n,
. Suppose that there exists such thatIf r < 1, then the series converges. If then the series diverges. If the ratio test is inconclusive, and the series may converge or diverge.
Root test or nth root test. Suppose that the terms of the sequence in question are non-negative. Define r as follows:
- where "lim sup" denotes the limit superior (possibly ∞; if the limit exists it is the same value).
If r < 1, then the series converges. If then the series diverges. If the root test is inconclusive, and the series may converge or diverge.
The ratio test and the root test are both based on comparison with a geometric series, and as such they work in similar situations. In fact, if the ratio test works (meaning that the limit exists and is not equal to 1) then so does the root test; the converse, however, is not true. The root test is therefore more generally applicable, but as a practical matter the limit is often difficult to compute for commonly seen types of series.
Integral test
Integral test for convergence
In mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. An early form of the test of convergence was developed in India by Madhava in the 14th century, and by his followers at the Kerala School...
. The series can be compared to an integral to establish convergence or divergence. Let
be a positive and monotone decreasing functionMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
. If
then the series converges. But if the integral diverges, then the series does so as well.
Limit comparison test
Limit comparison test
In mathematics, the limit comparison test is a method of testing for the convergence of an infinite series.- Statement :...
. If
, and the limit exists and is not zero, then converges if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
converges.Alternating series test
Alternating series test
The alternating series test is a method used to prove that infinite series of terms converge. It was discovered by Gottfried Leibniz and is sometimes known as Leibniz's test or the Leibniz criterion.A series of the form...
. Also known as the Leibniz criterion, the alternating series test
Alternating series test
The alternating series test is a method used to prove that infinite series of terms converge. It was discovered by Gottfried Leibniz and is sometimes known as Leibniz's test or the Leibniz criterion.A series of the form...
states that for an alternating series of the form
, if is monotone decreasing, and has a limit of 0 at infinity, then the series converges.Cauchy condensation test. If
is a monotone decreasing sequence, then converges if and only if converges.Dirichlet's test
Dirichlet's test
In mathematics, Dirichlet's test is a method of testing for the convergence of a series. It is named after mathematician Johann Dirichlet who published it in the Journal de Mathématiques Pures et Appliquées in 1862.- Statement :...
Abel's test
Abel's test
In mathematics, Abel's test is a method of testing for the convergence of an infinite series. The test is named after mathematician Niels Abel...
Raabe's test
Conditional and absolute convergence
, for all n. Therefore,This means that if
converges, then also converges (but not vice-versa).If the series
converges, then the series is absolutely convergent. An absolutely convergent sequence is one in which the length of the line created by joining together all of the increments to the partial sum is finitely long. The power series of the exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
is absolutely convergent everywhere.
If the series
converges but the series diverges, then the series is conditionally convergent. The path formed by connecting the partial sums of a conditionally convergent series is infinitely long. The power series of the logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is conditionally convergent.
The Riemann series theorem states that if a series converges conditionally, it is possible to rearrange the terms of the series in such a way that the series converges to any value, or even diverges.
Uniform convergence
- Main article: uniform convergence.
Let
be a sequence of functions.The series
is said to converge uniformly to fif the sequence
of partial sums defined by
converges uniformly to f.
There is an analogue of the comparison test for infinite series of functions called the Weierstrass M-test.
Cauchy convergence criterion
The Cauchy convergence criterion states that a seriesconverges if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the sequence of partial sums is a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
.
This means that for every
there is a positive integer such that for all we havewhich is equivalent to
External links
- Weisstein, Eric (2005). Riemann Series Theorem. Retrieved May 16, 2005.