Orders of approximation
Encyclopedia
In science
, engineering
, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation
is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order approximation, a second order approximation, and so forth.
Formally, an nth order approximation is one where the order of magnitude
of the error is at most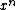
, or in terms of big O notation
, the error is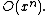
In suitable circumstances, approximating a function by a Taylor polynomial of degree n yields an nth order approximation, by Taylor's theorem
: a first order approximation is a linear approximation
, and so forth.
The term is also used more loosely, as detailed below.
s use for a first educated guess
at an answer. Many simplifying assumptions are made, and when a number is needed, an order of magnitude answer (or zero significant figures) is often given. For example, you might say "the town has a few thousand residents", when it has 3,914 people in actuality. This is also sometimes referred to as an order of magnitude
approximation.
A zeroth-order approximation of a function
(that is, mathematically
determining a formula
to fit multiple data point
s) will be constant
, or a flat line
with no slope
: a polynomial of degree 0. For example,
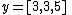
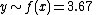
is an approximate fit to the data.
First-order approximation (also 1st order) is the term scientists use for a further educated guess at an answer. Some simplifying assumptions are made, and when a number is needed, an answer with only one significant figure is often given ("the town has 4×103 or four thousand residents").
A first-order approximation of a function (that is, mathematically determining a formula to fit multiple data points) will be a linear approximation
, straight line with a slope: a polynomial of degree 1. For example,
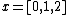
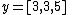
is an approximate fit to the data, obtained by simply averaging the y-values. Other methods for selecting a constant approximation can be used.
Second-order approximation (also 2nd order) is the term scientists use for a decent-quality answer. Few simplifying assumptions are made, and when a number is needed, an answer with two or more significant figures ("the town has 3.9×103 or thirty nine hundred residents") is generally given. In mathematical finance
, second-order approximations are known as convexity corrections.
A second-order approximation of a function (that is, mathematically determining a formula to fit multiple data points) will be a quadratic polynomial
, geometrically, a parabola
: a polynomial of degree 2. For example,
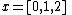
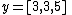
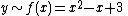
is an approximate fit to the data. In this case, with only three data points, a parabola is an exact fit.
While higher-order approximations exist and are crucial to a better understanding and description of reality, they are not typically referred to by number.
A third-order approximation would be required to fit four data points, and so on.
These terms are also used colloquially by scientists and engineers to describe phenomena that can be neglected as not significant (eg., "Of course the rotation of the earth affects our experiment, but it's such a high-order effect that we wouldn't be able to measure it" or "At these velocities, relativity is a fourth-order effect that we only worry about at the annual calibration.") In this usage, the ordinality of the approximation is not exact, but is used to emphasize its insignificance; the higher the number used, the less important the effect.
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order approximation, a second order approximation, and so forth.
Formally, an nth order approximation is one where the order of magnitude
Order of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
of the error is at most
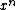, or in terms of big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, the error is
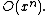
In suitable circumstances, approximating a function by a Taylor polynomial of degree n yields an nth order approximation, by Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
: a first order approximation is a linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
, and so forth.
The term is also used more loosely, as detailed below.
Usage in science and engineering
Zeroth-order approximation (also 0th order) is the term scientistScientist
A scientist in a broad sense is one engaging in a systematic activity to acquire knowledge. In a more restricted sense, a scientist is an individual who uses the scientific method. The person may be an expert in one or more areas of science. This article focuses on the more restricted use of the word...
s use for a first educated guess
Estimation
Estimation is the calculated approximation of a result which is usable even if input data may be incomplete or uncertain.In statistics,*estimation theory and estimator, for topics involving inferences about probability distributions...
at an answer. Many simplifying assumptions are made, and when a number is needed, an order of magnitude answer (or zero significant figures) is often given. For example, you might say "the town has a few thousand residents", when it has 3,914 people in actuality. This is also sometimes referred to as an order of magnitude
Order of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
approximation.
A zeroth-order approximation of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(that is, mathematically
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
determining a formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
to fit multiple data point
Data point
In statistics, a data point is a set of measurements on a single member of a statistical population, or a subset of those measurements for a given individual...
s) will be constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
, or a flat line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
with no slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
: a polynomial of degree 0. For example,
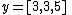
is an approximate fit to the data.
First-order approximation (also 1st order) is the term scientists use for a further educated guess at an answer. Some simplifying assumptions are made, and when a number is needed, an answer with only one significant figure is often given ("the town has 4×103 or four thousand residents").
A first-order approximation of a function (that is, mathematically determining a formula to fit multiple data points) will be a linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
, straight line with a slope: a polynomial of degree 1. For example,
is an approximate fit to the data, obtained by simply averaging the y-values. Other methods for selecting a constant approximation can be used.
Second-order approximation (also 2nd order) is the term scientists use for a decent-quality answer. Few simplifying assumptions are made, and when a number is needed, an answer with two or more significant figures ("the town has 3.9×103 or thirty nine hundred residents") is generally given. In mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, second-order approximations are known as convexity corrections.
A second-order approximation of a function (that is, mathematically determining a formula to fit multiple data points) will be a quadratic polynomial
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
, geometrically, a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
: a polynomial of degree 2. For example,
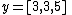
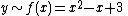
is an approximate fit to the data. In this case, with only three data points, a parabola is an exact fit.
While higher-order approximations exist and are crucial to a better understanding and description of reality, they are not typically referred to by number.
A third-order approximation would be required to fit four data points, and so on.
These terms are also used colloquially by scientists and engineers to describe phenomena that can be neglected as not significant (eg., "Of course the rotation of the earth affects our experiment, but it's such a high-order effect that we wouldn't be able to measure it" or "At these velocities, relativity is a fourth-order effect that we only worry about at the annual calibration.") In this usage, the ordinality of the approximation is not exact, but is used to emphasize its insignificance; the higher the number used, the less important the effect.