Linear equation - AbsoluteAstronomy.com

A linear equation is an algebraic equation in which each term

Term (mathematics)

A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...

is either a constant

Constant term

In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....

or the product of a constant and (the first power of) a single variable

Variable (mathematics)

In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...

.

Linear equations can have one or more variables. Linear equations occur with great regularity in applied mathematics

Applied mathematics

Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...

. While they arise quite naturally when modeling many phenomena, they are particularly useful since many non-linear equations may be reduced to linear equations by assuming that quantities of interest vary to only a small extent from some "background" state.

Linear equations in two variables

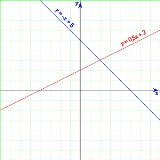
A common form of a linear equation in the two variables x and y is

where m and b designate constants. The origin of the name "linear" comes from the fact that the set of solutions of such an equation forms a straight line in the plane. In this particular equation, the constant m determines the slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

or gradient of that line, and the constant term

Constant term

"b" determines the point at which the line crosses the y-axis, otherwise known as the y-intercept.

Since terms of linear equations cannot contain products of distinct or equal variables, nor any power (other than 1) or other function of a variable, equations involving terms such as xy, x², y^1/3, and sin(x) are nonlinear.

Forms for 2D linear equations

Linear equations can be rewritten using the laws of elementary algebra

Elementary algebra

Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...

into several different forms. These equations are often referred to as the "equations of the straight line". In what follows x, y, t and θ are variables; other letters represent constant

Constant term

s (fixed numbers).

General form

where A and B are not both equal to zero. The equation is usually written so that A ≥ 0, by convention. The graph

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

of the equation is a straight line

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

, and every straight line can be represented by an equation in the above form. If A is nonzero, then the x-intercept, that is, the x-coordinate of the point where the graph crosses the x-axis (where, y is zero), is −C/A. If B is nonzero, then the y-intercept, that is the y-coordinate of the point where the graph crosses the y-axis (where x is zero), is −C/B, and the slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

of the line is −A/B.

Standard form

where A and B are not both equal to zero, A, B, and C are integers whose greatest common factor is 1, and A is nonnegative (if zero, B must be positive). The standard form can be converted to the general form, but not always to all the other forms if A or B is zero. It is worth noting that, while the term occurs frequently in school-level US algebra textbooks, most lines cannot be described by such equations. For instance, the line x + y = √2 cannot be described by a linear equation with integer coefficients since √2 is irrational.

Slope–intercept form

where m is the slope of the line and b is the y-intercept, which is the y-coordinate of the point where the line crosses the y axis. This can be seen by letting x = 0, which immediately gives y = b. It may be helpful to think about this in terms of y = b + mx; where the line originates at (0, b) and extends outward at a slope of m. Vertical lines, having undefined slope, cannot be represented by this form.

Point–slope form

where m is the slope of the line and (x₁,y₁) is any point on the line.

The point-slope form expresses the fact that the difference in the y coordinate between two points on a line (that is,

) is proportional to the difference in the x coordinate (that is,

). The proportionality constant is m (the slope of the line).

Two-point form

where

and

are two points on the line with

≠

. This is equivalent to the point-slope form above, where the slope is explicitly given as

Intercept form

where a and b must be nonzero. The graph of the equation has x-intercept a and y-intercept b. The intercept form can be converted to the standard form by setting A = 1/a, B = 1/b and C = 1.

Parametric form

and

Two simultaneous equations

Simultaneous equations

In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...

in terms of a variable parameter t, with slope m = V / T, x-intercept (VU−WT) / V and y-intercept (WT−VU) / T.

This can also be related to the two-point form, where T = p−h, U = h, V = q−k, and W = k:

and

In this case t varies from 0 at point (h,k) to 1 at point (p,q), with values of t between 0 and 1 providing interpolation

Interpolation

In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....

and other values of t providing extrapolation

Extrapolation

In mathematics, extrapolation is the process of constructing new data points. It is similar to the process of interpolation, which constructs new points between known points, but the results of extrapolations are often less meaningful, and are subject to greater uncertainty. It may also mean...

Polar form

where m is the slope of the line and b is the y-intercept

Y-intercept

In coordinate geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept is a point where the graph of a function or relation intersects with the y-axis of the coordinate system...

. When θ = 0 the graph will be undefined. The equation can be rewritten to eliminate discontinuities:

Normal form

The normal for a given line is defined to be the shortest segment between the line and the origin. The normal form of the equation of a straight line is given by:

where θ is the angle of inclination of the normal, and p is the length of the normal. The normal form can be derived from general form by dividing all of the coefficients by

This form is also called the Hesse standard form, after the German mathematician Ludwig Otto Hesse

Otto Hesse

Ludwig Otto Hesse was a German mathematician. Hesse was born in Königsberg, Prussia, and died in Munich, Bavaria. He worked on algebraic invariants...

Special cases

This is a special case of the standard form where A = 0 and B = 1, or of the slope-intercept form where the slope M = 0. The graph is a horizontal line with y-intercept equal to b. There is no x-intercept, unless b = 0, in which case the graph of the line is the x-axis, and so every real number is an x-intercept.

This is a special case of the standard form where A = 1 and B = 0. The graph is a vertical line with x-intercept equal to a. The slope is undefined. There is no y-intercept, unless a = 0, in which case the graph of the line is the y-axis, and so every real number is a y-intercept.

and

In this case all variables and constants have canceled out, leaving a trivially true statement. The original equation, therefore, would be called an identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...

and one would not normally consider its graph (it would be the entire xy-plane). An example is 2x + 4y = 2(x + 2y). The two expressions on either side of the equal sign are always equal, no matter what values are used for x and y.

In situations where algebraic manipulation leads to a statement such as 1 = 0, then the original equation is called inconsistent, meaning it is untrue for any values of x and y (i.e. its graph would be the empty set

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

) An example would be 3x + 2 = 3x − 5.

Connection with linear functions

A linear equation, written in the form y = f(x) whose graph crosses through the origin, that is whose y-intercept is 0, has the following properties:

and

where a is any scalar

Scalar (mathematics)

In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....

. A function which satisfies these properties is called a linear function (or linear operator, or more generally a linear map). However, linear equations that have non-zero y-intercepts will have neither property above and hence are not linear functions in this sense.

Linear equations in more than two variables

A linear equation can involve more than two variables. The general linear equation in n variables is:

In this form, a₁, a₂, …, a_n are the coefficients, x₁, x₂, …, x_n are the variables, and b is the constant. When dealing with three or fewer variables, it is common to replace x₁ with just x, x₂ with y, and x₃ with z, as appropriate.

Such an equation will represent an (n–1)-dimensional hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

in n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

(for example, a plane in 3-space).

In vector notation, this can be expressed as:

where

is a vector normal to the plane,

are the coordinates of any point on the plane, and

are the coordinates of the origin of the plane.

External links

Algebraic Equations at EqWorld: The World of Mathematical Equations.
http://video.google.com/videoplay?docid=-5991926520926012350# Video tutorial on solving one step to multistep equations

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Linear equations in two variables

Forms for 2D linear equations

General form

Standard form

Slope–intercept form

Point–slope form

Two-point form

Intercept form

Parametric form

Polar form

Normal form

Special cases

Connection with linear functions

Linear equations in more than two variables

See also

External links