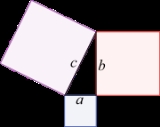
Pythagorean theorem
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
among the three sides of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
(right-angled triangle). In terms of areas, it states:
In any right angled triangle, the area of the square whose side is the hypotenuseHypotenuseIn geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
(the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angleRight angleIn geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
).
The theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
can be written as an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
relating the lengths of the sides a, b and c, often called the Pythagorean equation:
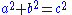
where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides.
The Pythagorean theorem is named after the Greek mathematician Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
, who by tradition is credited with its discovery and proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
, although it is often argued that knowledge of the theorem predates him.
Unanswered Questions

