Theorem
Encyclopedia
In mathematics
, a theorem is a statement
that has been proven
on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axiom
s. The derivation of a theorem is often interpreted as a proof of the truth of the resulting expression, but different deductive system
s can yield other interpretations, depending on the meanings of the derivation rules. The proof of a mathematical theorem is a logical argument demonstrating that the conclusions are a necessary consequence of the hypotheses, in the sense that if the hypotheses are true then the conclusions must also be true, without any further assumptions. The concept of a theorem is therefore fundamentally deductive, in contrast to the notion of a scientific theory
, which is empirical
.
Although they can be written in a completely symbolic form using, for example, propositional calculus
, theorems are often expressed in a natural language such as English. The same is true of proofs, which are often expressed as logically organized and clearly worded informal arguments, intended to convince readers of the truth of the statement of the theorem beyond any doubt, and from which arguments a formal symbolic proof can in principle be constructed. Such arguments are typically easier to check than purely symbolic ones — indeed, many mathematicians would express a preference for a proof that not only demonstrates the validity of a theorem, but also explains in some way why it is obviously true. In some cases, a picture alone may be sufficient to prove a theorem. Because theorems lie at the core of mathematics, they are also central to its aesthetics. Theorems are often described as being "trivial", or "difficult", or "deep", or even "beautiful". These subjective judgments vary not only from person to person, but also with time: for example, as a proof is simplified or better understood, a theorem that was once difficult may become trivial. On the other hand, a deep theorem may be simply stated, but its proof may involve surprising and subtle connections between disparate areas of mathematics. Fermat's Last Theorem
is a particularly well-known example of such a theorem.
: if A, then B. Such a theorem does not state that B is always true, only that B must be true if A is true. In this case A is called the hypothesis
of the theorem (note that "hypothesis" here is something very different from a conjecture
) and B the conclusion (A and B can also be denoted the antecedent and consequent). The theorem "If n is an even natural number
then n/2 is a natural number" is a typical example in which the hypothesis is that "n is an even natural number" and the conclusion is that "n/2 is also a natural number".
In order to be proven, a theorem must be expressible as a precise, formal statement. Nevertheless, theorems are usually expressed in natural language rather than in a completely symbolic form, with the intention that the reader will be able to produce a formal statement from the informal one.
It is common in mathematics to choose a number of hypotheses that are assumed to be true within a given theory, and then declare that the theory consists of all theorems provable using those hypotheses as assumptions. In this case the hypotheses that form the foundational basis are called the axioms (or postulates) of the theory. The field of mathematics known as proof theory
studies formal axiom systems and the proofs that can be performed within them.
Some theorems are "trivial," in the sense that they follow from definitions, axioms, and other theorems in obvious ways and do not contain any surprising insights. Some, on the other hand, may be called "deep": their proofs may be long and difficult, involve areas of mathematics superficially distinct from the statement of the theorem itself, or show surprising connections between disparate areas of mathematics. A theorem might be simple to state and yet be deep. An excellent example is Fermat's Last Theorem, and there are many other examples of simple yet deep theorems in number theory
and combinatorics
, among other areas.
There are other theorems for which a proof is known, but the proof cannot easily be written down. The most prominent examples are the four color theorem and the Kepler conjecture
. Both of these theorems are only known to be true by reducing them to a computational search which is then verified by a computer program. Initially, many mathematicians did not accept this form of proof, but it has become more widely accepted in recent years. The mathematician Doron Zeilberger
has even gone so far as to claim that these are possibly the only nontrivial results that mathematicians have ever proved. Many mathematical theorems can be reduced to more straightforward computation, including polynomial identities, trigonometric identities and hypergeometric identities.
Although the proof is necessary to produce a theorem, it is not usually considered part of the theorem. And even though more than one proof may be known for a single theorem, only one proof is required to establish the theorem's validity. The Pythagorean theorem and the law of quadratic reciprocity are contenders for the title of theorem with the greatest number of distinct proofs.
, especially in the field of proof theory, considers theorems as statements (called formula
s or well formed formulas) of a formal language. The statements of the language are strings of symbols and may be broadly divided into nonsense
and well-formed formulas. A set of deduction rules, also called transformation rules or rules of inference, must be provided. These deduction rules tell exactly when a formula can be derived from a set of premises. The set of well-formed formulas may be broadly divided into theorems and non-theorems. However, according to Hofstadter
, a formal system will often simply define all of its well-formed formula as theorems.
Different sets of derivation rules give rise to different interpretations of what it means for an expression to be a theorem. Some derivation rules and formal languages are intended to capture mathematical reasoning; the most common examples use first-order logic
. Other deductive systems describe term rewriting, such as the reduction rules for λ calculus
.
The definition of theorems as elements of a formal language allows for results in proof theory that study the structure of formal proofs and the structure of provable formulas. The most famous result is Gödel's incompleteness theorem; by representing theorems about basic number theory as expressions in a formal language, and then representing this language within number theory itself, Gödel constructed examples of statements that are neither provable nor disprovable from axiomatizations of number theory.
s. Any disagreement between prediction and experiment demonstrates the incorrectness of the scientific theory, or at least limits its accuracy or domain of validity. Mathematical theorems, on the other hand, are purely abstract formal statements: the proof of a theorem cannot involve experiments or other empirical evidence in the same way such evidence is used to support scientific theories.
Nonetheless, there is some degree of empiricism and data collection involved in the discovery of mathematical theorems. By establishing a pattern, sometimes with the use of a powerful computer, mathematicians may have an idea of what to prove, and in some cases even a plan for how to set about doing the proof. For example, the Collatz conjecture has been verified for start values up to about 2.88 × 1018. The Riemann hypothesis
has been verified for the first 10 trillion zeroes of the zeta function. Neither of these statements is considered to be proven.
Such evidence does not constitute proof. For example, the Mertens conjecture
is a statement about natural numbers that is now known to be false, but no explicit counterexample (i.e., a natural number n for which the Mertens function M(n) equals or exceeds the square root of n) is known: all numbers less than 1014 have the Mertens property, and the smallest number which does not have this property is only known to be less than the exponential
of 1.59 × 1040, which is approximately 10 to the power 4.3 × 1039. Since the number of particles in the universe is generally considered to be less than 10 to the power 100 (a googol
), there is no hope to find an explicit counterexample by exhaustive search.
Note that the word "theory" also exists in mathematics, to denote a body of mathematical axioms, definitions and theorems, as in, for example, group theory
. There are also "theorems" in science, particularly physics, and in engineering, but they often have statements and proofs in which physical assumptions and intuition play an important role; the physical axioms on which such "theorems" are based are themselves falsifiable.
There are other terms, less commonly used, which are conventionally attached to proven statements, so that certain theorems are referred to by historical or customary names. For examples:
A few well-known theorems have even more idiosyncratic names. The division algorithm
is a theorem expressing the outcome of division in the natural numbers and more general rings. The Banach–Tarski paradox
is a theorem in measure theory
that is paradox
ical in the sense that it contradicts common intuitions about volume in three-dimensional space.
An unproven statement that is believed to be true is called a conjecture (or sometimes a hypothesis, but with a different meaning from the one discussed above). To be considered a conjecture, a statement must usually be proposed publicly, at which point the name of the proponent may be attached to the conjecture, as with Goldbach's conjecture
. Other famous conjectures include the Collatz conjecture and the Riemann hypothesis.
The end of the proof may be signalled by the letters Q.E.D.
meaning "quod erat demonstrandum" or by one of the tombstone
marks "" or "" meaning "End of Proof", introduced by Paul Halmos
following their usage in magazine articles.
The exact style will depend on the author or publication. Many publications provide instructions or macros for typesetting in the house style.
It is common for a theorem to be preceded by definition
s describing the exact meaning of the terms used in the theorem. It is also common for a theorem to be preceded by a number of propositions or lemmas which are then used in the proof. However, lemmas are sometimes embedded in the proof of a theorem, either with nested proofs, or with their proofs presented after the proof of the theorem.
Corollaries to a theorem are either presented between the theorem and the proof, or directly after the proof. Sometimes corollaries have proofs of their own which explain why they follow from the theorem.
The well-known aphorism
, "A mathematician is a device for turning coffee into theorems", is probably due to Alfréd Rényi
, although it is often attributed to Rényi's colleague Paul Erdős
(and Rényi may have been thinking of Erdős), who was famous for the many theorems he produced, the number
of his collaborations, and his coffee drinking.
The classification of finite simple groups
is regarded by some to be the longest proof of a theorem; it comprises tens of thousands of pages in 500 journal articles by some 100 authors. These papers are together believed to give a complete proof, and there are several ongoing projects to shorten and simplify this proof. Another theorem of this type is the Four color theorem whose computer generated proof is too long to be read by a human. It is certainly the longest proof of a theorem whose statement can be easily understood by a layman.
(or "formalized"). A formal theorem is the purely formal analogue of a theorem. In general, a formal theorem is a type of well-formed formula
that satisfies certain logical and syntactic conditions. The notation
is often used to indicate that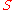 
is a theorem.
Formal theorems consist of formulas of a formal language and the transformation rules of a formal system. Specifically, a formal theorem is always the last formula of a derivation
in some formal system each formula of which is a logical consequence of the formulas which came before it in the derivation. The initially accepted formulas in the derivation are called its axioms, and are the basis on which the theorem is derived. A set of theorems is called a theory.
What makes formal theorems useful and of interest is that they can be interpreted
as true proposition
s and their derivations may be interpreted as a proof of the truth
of the resulting expression. A set of formal theorems may be referred to as a formal theory
. A theorem whose interpretation is a true statement about a formal system is called a metatheorem
.
are introduced. Different deductive systems may be constructed so as to yield other interpretations, depending on the presumptions of the derivation rules (i.e. belief
, justification
or other modalities
). The soundness
of a formal system depends on whether or not all of its theorems are also validities
. A validity is a formula that is true under any possible interpretation, e.g. in classical propositional logic validities are tautologies
. A formal system is considered semantically complete
when all of its tautologies are also theorems.
Its alphabet consists only of two symbols { A, B } and its formation rule for formulas is:
The single axiom of
is:
The only rule of inference
(transformation rule) for
is:
Theorems in
are defined as those formulae which have a derivation ending with that formula. For example
is a derivation. Therefore "ABBBAB" is a theorem of
The notion of truth (or falsity) cannot be applied to the formula "ABBBAB" until an interpretation is given to its symbols. Thus in this example, the formula does not yet represent a proposition, but is merely an empty abstraction.
Two metatheorems of
are:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a theorem is a statement
Statement (logic)
In logic a statement is either a meaningful declarative sentence that is either true or false, or what is asserted or made by the use of a declarative sentence...
that has been proven
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s. The derivation of a theorem is often interpreted as a proof of the truth of the resulting expression, but different deductive system
Deductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
s can yield other interpretations, depending on the meanings of the derivation rules. The proof of a mathematical theorem is a logical argument demonstrating that the conclusions are a necessary consequence of the hypotheses, in the sense that if the hypotheses are true then the conclusions must also be true, without any further assumptions. The concept of a theorem is therefore fundamentally deductive, in contrast to the notion of a scientific theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
, which is empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
.
Although they can be written in a completely symbolic form using, for example, propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
, theorems are often expressed in a natural language such as English. The same is true of proofs, which are often expressed as logically organized and clearly worded informal arguments, intended to convince readers of the truth of the statement of the theorem beyond any doubt, and from which arguments a formal symbolic proof can in principle be constructed. Such arguments are typically easier to check than purely symbolic ones — indeed, many mathematicians would express a preference for a proof that not only demonstrates the validity of a theorem, but also explains in some way why it is obviously true. In some cases, a picture alone may be sufficient to prove a theorem. Because theorems lie at the core of mathematics, they are also central to its aesthetics. Theorems are often described as being "trivial", or "difficult", or "deep", or even "beautiful". These subjective judgments vary not only from person to person, but also with time: for example, as a proof is simplified or better understood, a theorem that was once difficult may become trivial. On the other hand, a deep theorem may be simply stated, but its proof may involve surprising and subtle connections between disparate areas of mathematics. Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
is a particularly well-known example of such a theorem.
Informal accounts of theorems
Logically, many theorems are of the form of an indicative conditionalIndicative conditional
In natural languages, an indicative conditional is the logical operation given by statements of the form "If A then B". Unlike the material conditional, an indicative conditional does not have a stipulated definition...
: if A, then B. Such a theorem does not state that B is always true, only that B must be true if A is true. In this case A is called the hypothesis
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
of the theorem (note that "hypothesis" here is something very different from a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
) and B the conclusion (A and B can also be denoted the antecedent and consequent). The theorem "If n is an even natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
then n/2 is a natural number" is a typical example in which the hypothesis is that "n is an even natural number" and the conclusion is that "n/2 is also a natural number".
In order to be proven, a theorem must be expressible as a precise, formal statement. Nevertheless, theorems are usually expressed in natural language rather than in a completely symbolic form, with the intention that the reader will be able to produce a formal statement from the informal one.
It is common in mathematics to choose a number of hypotheses that are assumed to be true within a given theory, and then declare that the theory consists of all theorems provable using those hypotheses as assumptions. In this case the hypotheses that form the foundational basis are called the axioms (or postulates) of the theory. The field of mathematics known as proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
studies formal axiom systems and the proofs that can be performed within them.
Some theorems are "trivial," in the sense that they follow from definitions, axioms, and other theorems in obvious ways and do not contain any surprising insights. Some, on the other hand, may be called "deep": their proofs may be long and difficult, involve areas of mathematics superficially distinct from the statement of the theorem itself, or show surprising connections between disparate areas of mathematics. A theorem might be simple to state and yet be deep. An excellent example is Fermat's Last Theorem, and there are many other examples of simple yet deep theorems in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, among other areas.
There are other theorems for which a proof is known, but the proof cannot easily be written down. The most prominent examples are the four color theorem and the Kepler conjecture
Kepler conjecture
The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
. Both of these theorems are only known to be true by reducing them to a computational search which is then verified by a computer program. Initially, many mathematicians did not accept this form of proof, but it has become more widely accepted in recent years. The mathematician Doron Zeilberger
Doron Zeilberger
Doron Zeilberger is an Israeli mathematician, known for his work in combinatorics.He is a Board of Governors Professor of Mathematics at Rutgers University...
has even gone so far as to claim that these are possibly the only nontrivial results that mathematicians have ever proved. Many mathematical theorems can be reduced to more straightforward computation, including polynomial identities, trigonometric identities and hypergeometric identities.
Relation to proof
The notion of a theorem is deeply intertwined with the concept of proof. Indeed, theorems are true precisely in the sense that they possess proofs. Therefore, to establish a mathematical statement as a theorem, the existence of a line of reasoning from axioms in the system (and other, already established theorems) to the given statement must be demonstrated.Although the proof is necessary to produce a theorem, it is not usually considered part of the theorem. And even though more than one proof may be known for a single theorem, only one proof is required to establish the theorem's validity. The Pythagorean theorem and the law of quadratic reciprocity are contenders for the title of theorem with the greatest number of distinct proofs.
Theorems in logic
LogicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, especially in the field of proof theory, considers theorems as statements (called formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s or well formed formulas) of a formal language. The statements of the language are strings of symbols and may be broadly divided into nonsense
Nonsense
Nonsense is a communication, via speech, writing, or any other symbolic system, that lacks any coherent meaning. Sometimes in ordinary usage, nonsense is synonymous with absurdity or the ridiculous...
and well-formed formulas. A set of deduction rules, also called transformation rules or rules of inference, must be provided. These deduction rules tell exactly when a formula can be derived from a set of premises. The set of well-formed formulas may be broadly divided into theorems and non-theorems. However, according to Hofstadter
Douglas Hofstadter
Douglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
, a formal system will often simply define all of its well-formed formula as theorems.
Different sets of derivation rules give rise to different interpretations of what it means for an expression to be a theorem. Some derivation rules and formal languages are intended to capture mathematical reasoning; the most common examples use first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. Other deductive systems describe term rewriting, such as the reduction rules for λ calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
.
The definition of theorems as elements of a formal language allows for results in proof theory that study the structure of formal proofs and the structure of provable formulas. The most famous result is Gödel's incompleteness theorem; by representing theorems about basic number theory as expressions in a formal language, and then representing this language within number theory itself, Gödel constructed examples of statements that are neither provable nor disprovable from axiomatizations of number theory.
Relation with scientific theories
Theorems in mathematics and theories in science are fundamentally different in their epistemology. A scientific theory cannot be proven; its key attribute is that it is falsifiable, that is, it makes predictions about the natural world that are testable by experimentExperiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
s. Any disagreement between prediction and experiment demonstrates the incorrectness of the scientific theory, or at least limits its accuracy or domain of validity. Mathematical theorems, on the other hand, are purely abstract formal statements: the proof of a theorem cannot involve experiments or other empirical evidence in the same way such evidence is used to support scientific theories.
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
has been verified for the first 10 trillion zeroes of the zeta function. Neither of these statements is considered to be proven.
Such evidence does not constitute proof. For example, the Mertens conjecture
Mertens conjecture
In mathematics, the Mertens conjecture is the incorrect statement that the Mertens function M is bounded by √n, which implies the Riemann hypothesis...
is a statement about natural numbers that is now known to be false, but no explicit counterexample (i.e., a natural number n for which the Mertens function M(n) equals or exceeds the square root of n) is known: all numbers less than 1014 have the Mertens property, and the smallest number which does not have this property is only known to be less than the exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
of 1.59 × 1040, which is approximately 10 to the power 4.3 × 1039. Since the number of particles in the universe is generally considered to be less than 10 to the power 100 (a googol
Googol
A googol is the large number 10100, that is, the digit 1 followed by 100 zeros:The term was coined in 1938 by 9-year-old Milton Sirotta , nephew of American mathematician Edward Kasner...
), there is no hope to find an explicit counterexample by exhaustive search.
Note that the word "theory" also exists in mathematics, to denote a body of mathematical axioms, definitions and theorems, as in, for example, group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. There are also "theorems" in science, particularly physics, and in engineering, but they often have statements and proofs in which physical assumptions and intuition play an important role; the physical axioms on which such "theorems" are based are themselves falsifiable.
Terminology
A number of different terms for mathematical statements exist, these terms indicate the role statements play in a particular subject. The distinction between different terms is sometimes rather arbitrary and the usage of some terms has evolved over time.- An axiomAxiomIn traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
or postulate is a statement that is accepted without proof and regarded as fundamental to a subject. Historically these have been regarded as "self evident", but more recently they are considered assumptions that characterize the subject of study. In classical geometry, axioms are general statements while postulates are statements about geometrical objects. A definitionDefinitionA definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
is also accepted without proof since it simply gives the meaning of a word or phrase in terms of known concepts. - A propositionPropositionIn logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
is a generic term for a theorem of no particular importance. This term sometimes connotes a statement with a simple proof, while the term theorem is usually reserved for the most important results or those with long or difficult proofs. In classical geometry a proposition may be a construction that satisfies given requirements, for example Proposition 1 in Book I of Euclid's elements is the construction of an equilateral triangle. - A lemmaLemma (mathematics)In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
is a "helping theorem", a proposition with little applicability except that it forms part of the proof of a larger theorem. In some cases, as the relative importance of different theorems becomes more clear, what was once considered a lemma is now considered a theorem, though the word "lemma" remains in the name. Examples include Gauss's lemmaGauss's lemma (polynomial)In algebra, in the theory of polynomials , Gauss's lemma is either of two related statements about polynomials with integer coefficients:...
and Zorn's lemmaZorn's lemmaZorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
. - A corollaryCorollaryA corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
is a proposition that follows with little or no proof from one other theorem or definition.A converseConverse (logic)In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
of a theorem is a statement formed by replacing what is given in a theorem with what is to be proved. For example, the isosceles triangle theoremIsosceles triangle theoremIn Euclidean geometry, the isosceles triangle theorem, also known as the pons asinorum, states that the angles opposite the two equal sides of an isosceles triangle are equal...
states that if two sides of a triangle are equal then two angles are equal. In the converse the given, that two sides are equal, and what is to be proved, that two angles are equal, are swapped, so the converse is the statement that if two angles of a triangle are equal then two sides are equal. In this example the converse can be proven as another theorem but this is often not the case. For example the converse to the theorem that two right angles are equal angles is the statement that two equal angles must be right angles, and this is clearly not always the case.
There are other terms, less commonly used, which are conventionally attached to proven statements, so that certain theorems are referred to by historical or customary names. For examples:
- IdentityIdentity (mathematics)In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
, used for theorems which state an equality between two mathematical expressions. Examples include Euler's identity and Vandermonde's identity. - Rule, used for certain theorems such as Bayes' ruleBayes' ruleIn probability theory and applications, Bayes' rule relates the odds of event A_1 to event A_2, before and after conditioning on event B. The relationship is expressed in terms of the Bayes factor, \Lambda. Bayes' rule is derived from and closely related to Bayes' theorem...
and Cramer's ruleCramer's ruleIn linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
, that establish useful formulas. - Law. Examples include the law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, the law of cosinesLaw of cosinesIn trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
, and Kolmogorov's zero-one lawKolmogorov's zero-one lawIn probability theory, Kolmogorov's zero-one law, named in honor of Andrey Nikolaevich Kolmogorov, specifies that a certain type of event, called a tail event, will either almost surely happen or almost surely not happen; that is, the probability of such an event occurring is zero or one.Tail...
. - PrinciplePrincipleA principle is a law or rule that has to be, or usually is to be followed, or can be desirably followed, or is an inevitable consequence of something, such as the laws observed in nature or the way that a system is constructed...
. Examples include Harnack's principleHarnack's principleIn complex analysis, Harnack's principle or Harnack's theorem is one of several closely related theorems about the convergence of sequences of harmonic functions, that follow from Harnack's inequality.If the functions u_1, u_2, .....
, the least upper bound principle, and the pigeonhole principle.
A few well-known theorems have even more idiosyncratic names. The division algorithm
Division algorithm
In mathematics, and more particularly in arithmetic, the usual process of division of integers producing a quotient and a remainder can be specified precisely by a theorem stating that these exist uniquely with given properties. An integer division algorithm is any effective method for producing...
is a theorem expressing the outcome of division in the natural numbers and more general rings. The Banach–Tarski paradox
Banach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
is a theorem in measure theory
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
that is paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
ical in the sense that it contradicts common intuitions about volume in three-dimensional space.
An unproven statement that is believed to be true is called a conjecture (or sometimes a hypothesis, but with a different meaning from the one discussed above). To be considered a conjecture, a statement must usually be proposed publicly, at which point the name of the proponent may be attached to the conjecture, as with Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
. Other famous conjectures include the Collatz conjecture and the Riemann hypothesis.
Layout
A theorem and its proof are typically laid out as follows:- Theorem (name of person who proved it and year of discovery, proof or publication).
- Statement of theorem (sometimes called the proposition).
- Proof.
- Description of proof.
- End mark.
The end of the proof may be signalled by the letters Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
meaning "quod erat demonstrandum" or by one of the tombstone
Tombstone (typography)
The tombstone, halmos, or end of proof mark "" is used in mathematics to denote the end of a proof, in place of the traditional abbreviation "QED" for the Latin phrase "quod erat demonstrandum" ....
marks "" or "" meaning "End of Proof", introduced by Paul Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
following their usage in magazine articles.
The exact style will depend on the author or publication. Many publications provide instructions or macros for typesetting in the house style.
It is common for a theorem to be preceded by definition
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
s describing the exact meaning of the terms used in the theorem. It is also common for a theorem to be preceded by a number of propositions or lemmas which are then used in the proof. However, lemmas are sometimes embedded in the proof of a theorem, either with nested proofs, or with their proofs presented after the proof of the theorem.
Corollaries to a theorem are either presented between the theorem and the proof, or directly after the proof. Sometimes corollaries have proofs of their own which explain why they follow from the theorem.
Lore
It has been estimated that over a quarter of a million theorems are proved every year.The well-known aphorism
Aphorism
An aphorism is an original thought, spoken or written in a laconic and memorable form.The term was first used in the Aphorisms of Hippocrates...
, "A mathematician is a device for turning coffee into theorems", is probably due to Alfréd Rényi
Alfréd Rényi
Alfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
, although it is often attributed to Rényi's colleague Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
(and Rényi may have been thinking of Erdős), who was famous for the many theorems he produced, the number
Erdos number
The Erdős number describes the "collaborative distance" between a person and mathematician Paul Erdős, as measured by authorship of mathematical papers.The same principle has been proposed for other eminent persons in other fields.- Overview :...
of his collaborations, and his coffee drinking.
The classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
is regarded by some to be the longest proof of a theorem; it comprises tens of thousands of pages in 500 journal articles by some 100 authors. These papers are together believed to give a complete proof, and there are several ongoing projects to shorten and simplify this proof. Another theorem of this type is the Four color theorem whose computer generated proof is too long to be read by a human. It is certainly the longest proof of a theorem whose statement can be easily understood by a layman.
Formalized account of theorems
A theorem may be expressed in a formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
(or "formalized"). A formal theorem is the purely formal analogue of a theorem. In general, a formal theorem is a type of well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
that satisfies certain logical and syntactic conditions. The notation
is often used to indicate that 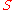is a theorem.Formal theorems consist of formulas of a formal language and the transformation rules of a formal system. Specifically, a formal theorem is always the last formula of a derivation
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
in some formal system each formula of which is a logical consequence of the formulas which came before it in the derivation. The initially accepted formulas in the derivation are called its axioms, and are the basis on which the theorem is derived. A set of theorems is called a theory.
What makes formal theorems useful and of interest is that they can be interpreted
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
as true proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s and their derivations may be interpreted as a proof of the truth
Truth
Truth has a variety of meanings, such as the state of being in accord with fact or reality. It can also mean having fidelity to an original or to a standard or ideal. In a common usage, it also means constancy or sincerity in action or character...
of the resulting expression. A set of formal theorems may be referred to as a formal theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
. A theorem whose interpretation is a true statement about a formal system is called a metatheorem
Metatheorem
In logic, a metatheorem is a statement about a formal system proven in a metalanguage. Unlike theorems proved within a given formal system, a metatheorem is proved within a metatheory, and may reference concepts that are present in the metatheory but not the object theory.- Discussion :A formal...
.
Syntax and semantics
The concept of a formal theorem is fundamentally syntactic, in contrast to the notion of a "true proposition" in which semanticsSemantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
are introduced. Different deductive systems may be constructed so as to yield other interpretations, depending on the presumptions of the derivation rules (i.e. belief
Belief
Belief is the psychological state in which an individual holds a proposition or premise to be true.-Belief, knowledge and epistemology:The terms belief and knowledge are used differently in philosophy....
, justification
Theory of justification
Theory of justification is a part of epistemology that attempts to understand the justification of propositions and beliefs. Epistemologists are concerned with various epistemic features of belief, which include the ideas of justification, warrant, rationality, and probability...
or other modalities
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
). The soundness
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
of a formal system depends on whether or not all of its theorems are also validities
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
. A validity is a formula that is true under any possible interpretation, e.g. in classical propositional logic validities are tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
. A formal system is considered semantically complete
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
when all of its tautologies are also theorems.
Derivation of a theorem
The notion of a theorem is very closely connected to its formal proof (also called a "derivation"). To illustrate how derivations are done, we will work in a very simplified formal system. Let us call ours Its alphabet consists only of two symbols { A, B } and its formation rule for formulas is:
- Any string of symbols of
which is at least 3 symbols long, and which is not infinitely long, is a formula. Nothing else is a formula.
The single axiom of
is:
- ABBA
The only rule of inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
(transformation rule) for
is:
- Any occurrence of "A" in a theorem may be replaced by an occurrence of the string "AB" and the result is a theorem.
Theorems in
are defined as those formulae which have a derivation ending with that formula. For example- ABBA (Given as axiom)
- ABBBA (by applying the transformation rule)
- ABBBAB (by applying the transformation rule)
is a derivation. Therefore "ABBBAB" is a theorem of
The notion of truth (or falsity) cannot be applied to the formula "ABBBAB" until an interpretation is given to its symbols. Thus in this example, the formula does not yet represent a proposition, but is merely an empty abstraction.Two metatheorems of
are:
- Every theorem begins with "A".
- Every theorem has exactly two "A"s.