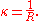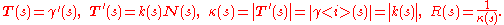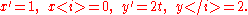Curvature
Encyclopedia
In mathematics
, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line
, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space (usually a Euclidean space
) in a way that relates to the radius of curvature of circles that touch the object, and intrinsic curvature
, which is defined at each point in a Riemannian manifold
. This article deals primarily with the first concept.
The canonical example of extrinsic curvature is that of a circle
, which everywhere has curvature equal to the reciprocal
of its radius
. Smaller circles bend more sharply, and hence have higher curvature. The curvature of a smooth curve is defined as the curvature of its osculating circle
at each point.
In a plane, this is a scalar
quantity, but in three or more dimensions it is described by a curvature vector that takes into account the direction of the bend as well as its sharpness. The curvature of more complex objects (such as surface
s or even curved n-dimensional space
s) is described by more complex objects from linear algebra
, such as the general Riemann curvature tensor
.
The remainder of this article discusses, from a mathematical perspective, some geometric examples of curvature: the curvature of a curve embedded in a plane and the curvature of a surface in Euclidean space.
See the links below for further reading.
(the precise technical assumptions are given below). The curvature of C at a point is a measure of how sensitive its tangent line is to moving the point to other nearby points. There are a number of equivalent ways that this idea can be made precise.
One way is geometrical. It is natural to define the curvature of a straight line to be identically zero. The curvature of a circle of radius R should be large if R is small and small if R is large. Thus the curvature of a circle is defined to be the reciprocal of the radius:
Given any curve C and a point P on it, there is a unique circle or line which most closely approximates the curve near P, the osculating circle
at P. The curvature of C at P is then defined to be the curvature of that circle or line. The radius of curvature is defined as the reciprocal of the curvature.
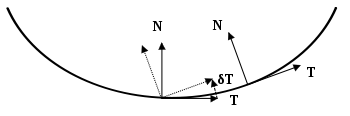
Another way to understand the curvature is physical. Suppose that a particle moves along the curve with unit speed. Taking the time s as the parameter for C, this provides a natural parametrization for the curve. The unit tangent vector T (which is also the velocity vector, since the particle is moving with unit speed) also depends on time. The curvature is then the magnitude of the rate of change of T. Symbolically,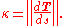
This is the magnitude of the acceleration of the particle. Geometrically, this measures how fast the unit tangent vector to the curve rotates. If a curve keeps close to the same direction, the unit tangent vector changes very little and the curvature is small; where the curve undergoes a tight turn, the curvature is large.
These two approaches to the curvature are related geometrically by the following observation. In the first definition, the curvature of a circle is equal to the ratio of the angle of an arc to its length. Likewise, the curvature of a plane curve at any point is the limiting ratio of dθ, an infinitesimal angle (in radians) between tangents to that curve at the ends of an infinitesimal segment of the curve, to the length of that segment ds, i.e., dθ/ds. If the tangents at the ends of the segment are represented by unit vectors, it is easy to show that in this limit, the magnitude of the difference vector is equal to dθ, which leads to the given expression in the second definition of curvature.
Suppose that C is a twice continuously differentiable immersed plane curve
, which here means that there exists parametric representation of C by a pair of functions such that the first and second derivatives of x and y both exist and are continuous, and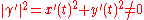
throughout the domain. For a such a plane curve, there exists a reparametrization with respect to arc length
s. This is a parametrization of C such that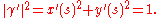
The velocity vector T(s) is the unit tangent vector. The unit normal vector N(s), the curvature κ(s), the oriented or signed curvature k(s), and the radius of curvature R(s) are given by
Expressions for calculating the curvature in arbitrary coordinate systems are given below.
The signed curvature depends on the particular parametrization chosen for a curve. For example the unit circle can be parametrised by (counterclockwise, with k > 0), or by (clockwise, with k < 0). More precisely, the signed curvature depends only on the choice of orientation
of an immersed curve. Every immersed curve in the plane admits two possible orientations.
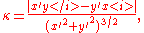
where primes refer to derivatives with respect to parameter t . The signed curvature k is
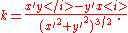
These can be expressed in a coordinate-independent manner via
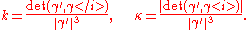
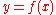, and now using primes for derivatives with respect to coordinate x , the curvature is
,
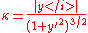and the signed curvature is
.
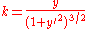This quantity is common in physics
and engineering
; for example, in the equations of bending
in beams, the 1D vibration
of a tense string, approximations to the fluid flow around surfaces (in aeronautics), and the free surface boundary conditions in ocean waves. In such applications, the assumption is almost always made that the slope
is small compared with unity, so that the approximation:
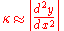
may be used. This approximation yields a straightforward linear equation describing the phenomenon, which would otherwise remain intractable.
If a curve is defined in polar coordinates as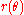
, then its curvature is
where here the prime now refers to differentiation with respect to
.
. We can parametrize the curve simply as . If we use primes for derivatives with respect to parameter t , then
Substituting and dropping unnecessary absolute values, get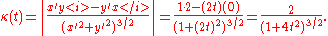
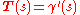
and the curvature is the magnitude of the acceleration: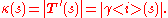
The direction of the acceleration is the unit normal vector N(s), which is defined by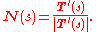
The plane containing the two vectors T(s) and N(s) is called the osculating plane to the curve at γ(s). The curvature has the following geometrical interpretation. There exists a circle in the osculating plane tangent to γ(s) whose Taylor series to second order at the point of contact agrees with that of γ(s). This is the osculating circle to the curve. The radius of the circle R(s) is called the radius of curvature, and the curvature is the reciprocal of the radius of curvature:
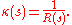
The tangent, curvature, and normal vector together describe the second-order behavior of a curve near a point. In three-dimensions, the third order behavior of a curve is described by a related notion of torsion
, which measures the extent to which a curve tends to perform a corkscrew in space. The torsion and curvature are related by the Frenet–Serret formulas (in three dimensions) and their generalization
(in higher dimensions).
the curvature is
where the prime denotes differentiation with respect to time t. This can be expressed independently of the coordinate system by means of the formula
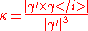
where
is the vector cross product
. Equivalently,
Here the t denotes the matrix transpose. This last formula is also valid for the curvature of curves in a Euclidean space of any dimension.
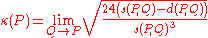
where the limit is taken as the point Q approaches P on C. The denominator can equally well be taken to be d(P,Q)3. The formula is valid in any dimension. Furthermore, by considering the limit independently on either side of P, this definition of the curvature can sometimes accommodate a singularity at P. The formula follows by verifying it for the osculating circle.
, further measures of curvature are
available, which take the surface's unit-normal vector, u into account. These are the normal curvature, geodesic curvature
and geodesic torsion.
Any non-singular curve on a smooth surface will have its tangent vector T lying in the tangent plane of the surface orthogonal
to the normal vector. The normal curvature, kn, is the curvature of the curve projected onto the plane containing the curve's tangent T and the surface normal u; the geodesic curvature, kg, is the curvature of the curve projected onto the
surface's tangent plane; and the geodesic torsion (or relative torsion), τr, measures the rate of change of the surface normal around the curve's tangent.
Let the curve be a unit speed curve and let t = u × T so that T, u, t form an orthonormal basis
: the Darboux frame
. The above quantities are related by: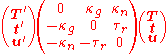
All curves with the same tangent vector will have the same normal curvature, which is the same as the curvature of the curve obtained by intersecting the surface with the plane containing T and u. Taking all possible tangent vectors
then the maximum and minimum values of the normal curvature at a point are called the principal curvature
s, k1 and k2, and the directions of the corresponding tangent vectors are called principal directions.
, named after Carl Friedrich Gauss
, is equal to the product of the principal curvatures, k1k2. It has the dimension of 1/length2 and is positive for sphere
s, negative for one-sheet hyperboloids and zero for planes. It determines whether a surface is locally convex (when it is positive) or locally saddle (when it is negative).
This definition of Gaussian curvature is extrinsic in that it uses the surface's embedding
in R3, normal vectors, external planes etc. Gaussian curvature is however in fact an intrinsic property of the surface, meaning it does not depend on the particular embedding
of the surface; intuitively, this means that ants living on the surface could determine the Gaussian curvature. For example, an ant living on a sphere could measure the sum of the interior angles of a triangle and determine that it was greater than 180 degrees, implying that the space it inhabited had positive curvature. On the other hand, an ant living on a cylinder would not detect any such departure from Euclidean geometry
, in particular the ant could not detect that the two surfaces have different mean curvatures (see below) which is a purely extrinsic type of curvature.
Formally, Gaussian curvature only depends on the Riemannian metric of the surface. This is Gauss
's celebrated Theorema Egregium
, which he found while concerned with geographic surveys and mapmaking.
An intrinsic definition of the Gaussian curvature at a point P is the following: imagine an ant which is tied to P with a short thread of length r. She runs around P while the thread is completely stretched and measures the length C(r) of one complete trip around P. If the surface were flat, she would find C(r) = 2πr. On curved surfaces, the formula for C(r) will be different, and the Gaussian curvature K at the point P can be computed by the Bertrand–Diquet–Puiseux theorem
as
The integral
of the Gaussian curvature over the whole surface is closely related to the surface's Euler characteristic
; see the Gauss-Bonnet theorem.
The discrete analog of curvature, corresponding to curvature being concentrated at a point and particularly useful for polyhedra, is the (angular) defect
; the analog for the Gauss-Bonnet theorem is Descartes' theorem on total angular defect.
Because curvature can be defined without reference to an embedding space, it is not necessary that a surface be embedded in a higher dimensional space in order to be curved. Such an intrinsically curved two-dimensional surface is a simple example of a Riemannian manifold
.
is equal to half the sum of the principal curvature
s, (k1+k2)/2. It has the dimension of 1/length. Mean curvature is closely related to the first variation of surface area
, in particular a minimal surface
such as a soap film
, has mean curvature zero and a soap bubble
has constant mean curvature. Unlike Gauss curvature, the mean curvature is extrinsic and depends on the embedding, for instance, a cylinder
and a plane are locally isometric
but the mean curvature of a plane is zero while that of a cylinder is nonzero.
in the tangent plane to the surface at a point whose value at a particular tangent vector X to the surface is the normal component of the acceleration of a curve along the surface tangent to X; that is, it is the normal curvature to a curve tangent to X (see above). Symbolically,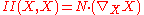
where N is the unit normal to the surface. For unit tangent vectors X, the second fundamental form assumes the maximum value k1 and minimum value k2, which occur in the principal directions u1 and u2, respectively. Thus, by the principal axis theorem
, the second fundamental form is
Thus the second fundamental form encodes both the intrinsic and extrinsic curvatures.
A related notion of curvature is the shape operator, which is a linear operator from the tangent plane to itself. When applied to a tangent vector X to the surface, the shape operator is the tangential component of the rate of change of the normal vector when moved along a curve on the surface tangent to X. The principal curvatures are the eigenvalues of the shape operator, and in fact the shape operator and second fundamental form have the same matrix representation with respect to a pair of orthonormal vectors of the tangent plane. The Gauss curvature is thus the determinant
of the shape tensor and the mean curvature is half its trace
.
. Again, the curved space may or may not be conceived as being embedded in a higher-dimensional space.
After the discovery of the intrinsic definition of curvature, which is closely connected with non-Euclidean geometry
, many mathematicians and scientists questioned whether ordinary physical space might be curved, although the success of Euclidean geometry up to that time meant that the radius of curvature must be astronomically large. In the theory of general relativity
, which describes gravity and cosmology
, the idea is slightly generalised to the "curvature of space-time"; in relativity theory space-time is a pseudo-Riemannian manifold
. Once a time coordinate is defined, the three-dimensional space corresponding to a particular time is generally a curved Riemannian manifold; but since the time coordinate choice is largely arbitrary, it is the underlying space-time curvature that is physically significant.
Although an arbitrarily-curved space is very complex to describe, the curvature of a space which is locally isotropic and homogeneous
is described by a single Gaussian curvature, as for a surface; mathematically these are strong conditions, but they correspond to reasonable physical assumptions (all points and all directions are indistinguishable). A positive curvature corresponds to the inverse square radius of curvature; an example is a sphere or hypersphere
. An example of negatively curved space is hyperbolic geometry
. A space or space-time with zero curvature is called flat. For example, Euclidean space
is an example of a flat space, and Minkowski space
is an example of a flat space-time. There are other examples of flat geometries in both settings, though. A torus
or a cylinder
can both be given flat metrics, but differ in their topology
. Other topologies are also possible for curved space. See also shape of the universe
.
The mathematical notion of curvature is also defined in much more general contexts. Many of these generalizations emphasize different aspects of the curvature as it is understood in lower dimensions.
One such generalization is kinematic. The curvature of a curve can naturally be considered as a kinematic quantity, representing the force felt by a certain observer moving along the curve; analogously, curvature in higher dimensions can be regarded as a kind of tidal force
(this is one way of thinking of the sectional curvature
). This generalization of curvature depends on how nearby test particles diverge or converge when they are allowed to move freely in the space; see Jacobi field
.
Another broad generalization of curvature comes from the study of parallel transport
on a surface. For instance, if a vector is moved around a loop on the surface of a sphere keeping parallel throughout the motion, then the final position of the vector may not be the same as the initial position of the vector. This phenomenon is known as holonomy
. Various generalizations capture in an abstract form this idea of curvature as a measure of holonomy; see curvature form
. A closely related notion of curvature comes from gauge theory
in physics, where the curvature represents a field and a vector potential
for the field is a quantity that is in general path-dependent: it may change if an observer moves around a loop.
Two more generalizations of curvature are the scalar curvature
and Ricci curvature
. In a curved surface such as the sphere, the area of a disc on the surface differs from the area of a disc of the same radius in flat space. This difference (in a suitable limit) is measured by the scalar curvature. The difference in area of a sector of the disc is measured by the Ricci curvature. Each of the scalar curvature and Ricci curvature are defined in analogous ways in three and higher dimensions. They are particularly important in relativity theory, where they both appear on the side of Einstein's field equations that represents the geometry of spacetime (the other side of which represents the presence of matter and energy). These generalizations of curvature underlie, for instance, the notion that curvature can be a property of a measure
; see curvature of a measure
.
Another generalization of curvature relies on the ability to compare
a curved space with another space that has constant curvature. Often this is done with triangles in the spaces. The notion of a triangle makes senses in metric space
s, and this gives rise to CAT(k) space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space (usually a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
) in a way that relates to the radius of curvature of circles that touch the object, and intrinsic curvature
Curvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
, which is defined at each point in a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. This article deals primarily with the first concept.
The canonical example of extrinsic curvature is that of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, which everywhere has curvature equal to the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of its radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
. Smaller circles bend more sharply, and hence have higher curvature. The curvature of a smooth curve is defined as the curvature of its osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
at each point.
In a plane, this is a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
quantity, but in three or more dimensions it is described by a curvature vector that takes into account the direction of the bend as well as its sharpness. The curvature of more complex objects (such as surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s or even curved n-dimensional space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
s) is described by more complex objects from linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, such as the general Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
.
The remainder of this article discusses, from a mathematical perspective, some geometric examples of curvature: the curvature of a curve embedded in a plane and the curvature of a surface in Euclidean space.
See the links below for further reading.
Curvature of plane curves
Let C be a plane curvePlane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
(the precise technical assumptions are given below). The curvature of C at a point is a measure of how sensitive its tangent line is to moving the point to other nearby points. There are a number of equivalent ways that this idea can be made precise.
Given any curve C and a point P on it, there is a unique circle or line which most closely approximates the curve near P, the osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
at P. The curvature of C at P is then defined to be the curvature of that circle or line. The radius of curvature is defined as the reciprocal of the curvature.
Another way to understand the curvature is physical. Suppose that a particle moves along the curve with unit speed. Taking the time s as the parameter for C, this provides a natural parametrization for the curve. The unit tangent vector T (which is also the velocity vector, since the particle is moving with unit speed) also depends on time. The curvature is then the magnitude of the rate of change of T. Symbolically,
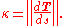
This is the magnitude of the acceleration of the particle. Geometrically, this measures how fast the unit tangent vector to the curve rotates. If a curve keeps close to the same direction, the unit tangent vector changes very little and the curvature is small; where the curve undergoes a tight turn, the curvature is large.
These two approaches to the curvature are related geometrically by the following observation. In the first definition, the curvature of a circle is equal to the ratio of the angle of an arc to its length. Likewise, the curvature of a plane curve at any point is the limiting ratio of dθ, an infinitesimal angle (in radians) between tangents to that curve at the ends of an infinitesimal segment of the curve, to the length of that segment ds, i.e., dθ/ds. If the tangents at the ends of the segment are represented by unit vectors, it is easy to show that in this limit, the magnitude of the difference vector is equal to dθ, which leads to the given expression in the second definition of curvature.
Precise definition
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
, which here means that there exists parametric representation of C by a pair of functions such that the first and second derivatives of x and y both exist and are continuous, and
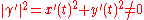
throughout the domain. For a such a plane curve, there exists a reparametrization with respect to arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
s. This is a parametrization of C such that
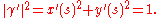
The velocity vector T(s) is the unit tangent vector. The unit normal vector N(s), the curvature κ(s), the oriented or signed curvature k(s), and the radius of curvature R(s) are given by
Expressions for calculating the curvature in arbitrary coordinate systems are given below.
Signed curvature
The sign of the signed curvature k indicates the direction in which the unit tangent vector rotates as a function of the parameter along the curve. If the unit tangent rotates counterclockwise, then k > 0. If it rotates clockwise, then k < 0.The signed curvature depends on the particular parametrization chosen for a curve. For example the unit circle can be parametrised by (counterclockwise, with k > 0), or by (clockwise, with k < 0). More precisely, the signed curvature depends only on the choice of orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of an immersed curve. Every immersed curve in the plane admits two possible orientations.
Local expressions
For a plane curve given parametrically in Cartesian coordinates as , the curvature is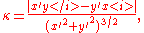where primes refer to derivatives with respect to parameter t . The signed curvature k is
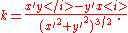
These can be expressed in a coordinate-independent manner via
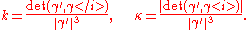
Curvature of a graph
For the less general case of a plane curve given explicitly as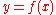, and now using primes for derivatives with respect to coordinate x , the curvature is 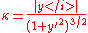,and the signed curvature is
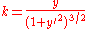.This quantity is common in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
; for example, in the equations of bending
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
in beams, the 1D vibration
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
of a tense string, approximations to the fluid flow around surfaces (in aeronautics), and the free surface boundary conditions in ocean waves. In such applications, the assumption is almost always made that the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
is small compared with unity, so that the approximation:
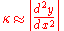
may be used. This approximation yields a straightforward linear equation describing the phenomenon, which would otherwise remain intractable.
If a curve is defined in polar coordinates as
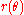, then its curvature iswhere here the prime now refers to differentiation with respect to
.Example
Consider the parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. We can parametrize the curve simply as . If we use primes for derivatives with respect to parameter t , then
Substituting and dropping unnecessary absolute values, get
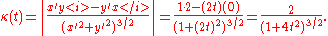
Curvature of space curves
As in the case of curves in two dimensions, the curvature of a regular space curve C in three dimensions (and higher) is the magnitude of the acceleration of a particle moving with unit speed along a curve. Thus if γ(s) is the arclength parametrization of C then the unit tangent vector T(s) is given by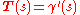and the curvature is the magnitude of the acceleration:
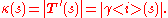
The direction of the acceleration is the unit normal vector N(s), which is defined by
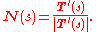
The plane containing the two vectors T(s) and N(s) is called the osculating plane to the curve at γ(s). The curvature has the following geometrical interpretation. There exists a circle in the osculating plane tangent to γ(s) whose Taylor series to second order at the point of contact agrees with that of γ(s). This is the osculating circle to the curve. The radius of the circle R(s) is called the radius of curvature, and the curvature is the reciprocal of the radius of curvature:
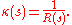
The tangent, curvature, and normal vector together describe the second-order behavior of a curve near a point. In three-dimensions, the third order behavior of a curve is described by a related notion of torsion
Torsion of curves
In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting. Taken together,the curvature and the torsion of a space curve are analogous to the curvature of a plane curve...
, which measures the extent to which a curve tends to perform a corkscrew in space. The torsion and curvature are related by the Frenet–Serret formulas (in three dimensions) and their generalization
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
(in higher dimensions).
Local expressions
For a parametrically defined space curve in three-dimensions given in Cartesian coordinates by ,the curvature is
where the prime denotes differentiation with respect to time t. This can be expressed independently of the coordinate system by means of the formula
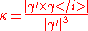
where
is the vector cross productCross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. Equivalently,
Here the t denotes the matrix transpose. This last formula is also valid for the curvature of curves in a Euclidean space of any dimension.
Curvature from arc and chord length
Given two points P and Q on C, let s(P,Q) be the arc length of the portion of the curve between P and Q and let d(P,Q) denote the length of the line segment from P to Q. The curvature of C at P is given by the limit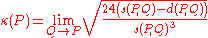where the limit is taken as the point Q approaches P on C. The denominator can equally well be taken to be d(P,Q)3. The formula is valid in any dimension. Furthermore, by considering the limit independently on either side of P, this definition of the curvature can sometimes accommodate a singularity at P. The formula follows by verifying it for the osculating circle.
Curves on surfaces
When a one dimensional curve lies on a two dimensional surface embedded in three dimensions R3Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, further measures of curvature are
available, which take the surface's unit-normal vector, u into account. These are the normal curvature, geodesic curvature
Geodesic curvature
In Riemannian geometry, the geodesic curvature k_g of a curve lying on a submanifold of the ambient space measures how far the curve is from being a geodesic...
and geodesic torsion.
Any non-singular curve on a smooth surface will have its tangent vector T lying in the tangent plane of the surface orthogonal
to the normal vector. The normal curvature, kn, is the curvature of the curve projected onto the plane containing the curve's tangent T and the surface normal u; the geodesic curvature, kg, is the curvature of the curve projected onto the
surface's tangent plane; and the geodesic torsion (or relative torsion), τr, measures the rate of change of the surface normal around the curve's tangent.
Let the curve be a unit speed curve and let t = u × T so that T, u, t form an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
: the Darboux frame
Darboux frame
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space...
. The above quantities are related by:
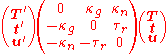
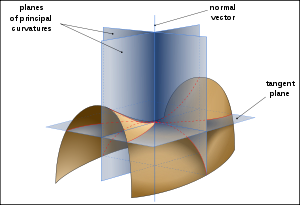
Principal curvature
then the maximum and minimum values of the normal curvature at a point are called the principal curvature
Principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
s, k1 and k2, and the directions of the corresponding tangent vectors are called principal directions.
Gaussian curvature
In contrast to curves, which do not have intrinsic curvature, but do have extrinsic curvature (they only have a curvature given an embedding), surfaces can have intrinsic curvature, independent of an embedding. The Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, named after Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, is equal to the product of the principal curvatures, k1k2. It has the dimension of 1/length2 and is positive for sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s, negative for one-sheet hyperboloids and zero for planes. It determines whether a surface is locally convex (when it is positive) or locally saddle (when it is negative).
This definition of Gaussian curvature is extrinsic in that it uses the surface's embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in R3, normal vectors, external planes etc. Gaussian curvature is however in fact an intrinsic property of the surface, meaning it does not depend on the particular embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of the surface; intuitively, this means that ants living on the surface could determine the Gaussian curvature. For example, an ant living on a sphere could measure the sum of the interior angles of a triangle and determine that it was greater than 180 degrees, implying that the space it inhabited had positive curvature. On the other hand, an ant living on a cylinder would not detect any such departure from Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, in particular the ant could not detect that the two surfaces have different mean curvatures (see below) which is a purely extrinsic type of curvature.
Formally, Gaussian curvature only depends on the Riemannian metric of the surface. This is Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's celebrated Theorema Egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
, which he found while concerned with geographic surveys and mapmaking.
An intrinsic definition of the Gaussian curvature at a point P is the following: imagine an ant which is tied to P with a short thread of length r. She runs around P while the thread is completely stretched and measures the length C(r) of one complete trip around P. If the surface were flat, she would find C(r) = 2πr. On curved surfaces, the formula for C(r) will be different, and the Gaussian curvature K at the point P can be computed by the Bertrand–Diquet–Puiseux theorem
Bertrand–Diquet–Puiseux theorem
In the mathematical study of the differential geometry of surfaces, the Bertrand–Diquet–Puiseux theoremexpresses the Gaussian curvature of a surface in terms of the circumference of a geodesic circle, or the area of a geodesic disc. The theorem is named for Joseph Bertrand, Victor Puiseux, and...
as
The integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the Gaussian curvature over the whole surface is closely related to the surface's Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
; see the Gauss-Bonnet theorem.
The discrete analog of curvature, corresponding to curvature being concentrated at a point and particularly useful for polyhedra, is the (angular) defect
Defect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
; the analog for the Gauss-Bonnet theorem is Descartes' theorem on total angular defect.
Because curvature can be defined without reference to an embedding space, it is not necessary that a surface be embedded in a higher dimensional space in order to be curved. Such an intrinsically curved two-dimensional surface is a simple example of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
.
Mean curvature
The mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
is equal to half the sum of the principal curvature
Principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
s, (k1+k2)/2. It has the dimension of 1/length. Mean curvature is closely related to the first variation of surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
, in particular a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
such as a soap film
Soap film
Soap films are thin layers of liquid surrounded by air. For example, if two soap bubbles enters in contact, they merged and a thin film is created in between. Thus, foams are composed of a network of films connected by Plateau borders...
, has mean curvature zero and a soap bubble
Soap bubble
A soap bubble is a thin film of soapy water enclosing air, that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds before bursting, either on their own or on contact with another object. They are often used for children's enjoyment, but they are also...
has constant mean curvature. Unlike Gauss curvature, the mean curvature is extrinsic and depends on the embedding, for instance, a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
and a plane are locally isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
but the mean curvature of a plane is zero while that of a cylinder is nonzero.
Second fundamental form
The intrinsic and extrinsic curvature of a surface can be combined in the second fundamental form. This is a quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
in the tangent plane to the surface at a point whose value at a particular tangent vector X to the surface is the normal component of the acceleration of a curve along the surface tangent to X; that is, it is the normal curvature to a curve tangent to X (see above). Symbolically,
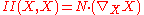
where N is the unit normal to the surface. For unit tangent vectors X, the second fundamental form assumes the maximum value k1 and minimum value k2, which occur in the principal directions u1 and u2, respectively. Thus, by the principal axis theorem
Principal axis theorem
In the mathematical fields of geometry and linear algebra, a principal axis is a certain line in a Euclidean space associated to an ellipsoid or hyperboloid, generalizing the major and minor axes of an ellipse...
, the second fundamental form is
Thus the second fundamental form encodes both the intrinsic and extrinsic curvatures.
A related notion of curvature is the shape operator, which is a linear operator from the tangent plane to itself. When applied to a tangent vector X to the surface, the shape operator is the tangential component of the rate of change of the normal vector when moved along a curve on the surface tangent to X. The principal curvatures are the eigenvalues of the shape operator, and in fact the shape operator and second fundamental form have the same matrix representation with respect to a pair of orthonormal vectors of the tangent plane. The Gauss curvature is thus the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the shape tensor and the mean curvature is half its trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
.
Higher dimensions: Curvature of space
By extension of the former argument, a space of three or more dimensions can be intrinsically curved; the full mathematical description is described at curvature of Riemannian manifoldsCurvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
. Again, the curved space may or may not be conceived as being embedded in a higher-dimensional space.
After the discovery of the intrinsic definition of curvature, which is closely connected with non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, many mathematicians and scientists questioned whether ordinary physical space might be curved, although the success of Euclidean geometry up to that time meant that the radius of curvature must be astronomically large. In the theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, which describes gravity and cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
, the idea is slightly generalised to the "curvature of space-time"; in relativity theory space-time is a pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
. Once a time coordinate is defined, the three-dimensional space corresponding to a particular time is generally a curved Riemannian manifold; but since the time coordinate choice is largely arbitrary, it is the underlying space-time curvature that is physically significant.
Although an arbitrarily-curved space is very complex to describe, the curvature of a space which is locally isotropic and homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
is described by a single Gaussian curvature, as for a surface; mathematically these are strong conditions, but they correspond to reasonable physical assumptions (all points and all directions are indistinguishable). A positive curvature corresponds to the inverse square radius of curvature; an example is a sphere or hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
. An example of negatively curved space is hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. A space or space-time with zero curvature is called flat. For example, Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is an example of a flat space, and Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
is an example of a flat space-time. There are other examples of flat geometries in both settings, though. A torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
or a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
can both be given flat metrics, but differ in their topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Other topologies are also possible for curved space. See also shape of the universe
Shape of the Universe
The shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...
.
Generalizations
One such generalization is kinematic. The curvature of a curve can naturally be considered as a kinematic quantity, representing the force felt by a certain observer moving along the curve; analogously, curvature in higher dimensions can be regarded as a kind of tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
(this is one way of thinking of the sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
). This generalization of curvature depends on how nearby test particles diverge or converge when they are allowed to move freely in the space; see Jacobi field
Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
.
Another broad generalization of curvature comes from the study of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
on a surface. For instance, if a vector is moved around a loop on the surface of a sphere keeping parallel throughout the motion, then the final position of the vector may not be the same as the initial position of the vector. This phenomenon is known as holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
. Various generalizations capture in an abstract form this idea of curvature as a measure of holonomy; see curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
. A closely related notion of curvature comes from gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
in physics, where the curvature represents a field and a vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
for the field is a quantity that is in general path-dependent: it may change if an observer moves around a loop.
Two more generalizations of curvature are the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
and Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
. In a curved surface such as the sphere, the area of a disc on the surface differs from the area of a disc of the same radius in flat space. This difference (in a suitable limit) is measured by the scalar curvature. The difference in area of a sector of the disc is measured by the Ricci curvature. Each of the scalar curvature and Ricci curvature are defined in analogous ways in three and higher dimensions. They are particularly important in relativity theory, where they both appear on the side of Einstein's field equations that represents the geometry of spacetime (the other side of which represents the presence of matter and energy). These generalizations of curvature underlie, for instance, the notion that curvature can be a property of a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
; see curvature of a measure
Curvature of a measure
In mathematics, the curvature of a measure defined on the Euclidean plane R2 is a quantification of how much the measure's "distribution of mass" is "curved". It is related to notions of curvature in geometry. In the form presented below, the concept was introduced in 1995 by the mathematician Mark S...
.
Another generalization of curvature relies on the ability to compare
Comparison theorem
A comparison theorem is any of a variety of theorems that compare properties of various mathematical objects.-Riemannian geometry:In Riemannian geometry it is a traditional name for a number of theorems that compare various metrics and provide various estimates in Riemannian geometry.*Rauch...
a curved space with another space that has constant curvature. Often this is done with triangles in the spaces. The notion of a triangle makes senses in metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, and this gives rise to CAT(k) space
CAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
s.
See also
- Curvature formCurvature formIn differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
for the appropriate notion of curvature for vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s and principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s with connectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
. - Curvature of a measureCurvature of a measureIn mathematics, the curvature of a measure defined on the Euclidean plane R2 is a quantification of how much the measure's "distribution of mass" is "curved". It is related to notions of curvature in geometry. In the form presented below, the concept was introduced in 1995 by the mathematician Mark S...
for a notion of curvature in measure theory. - Curvature of Riemannian manifoldsCurvature of Riemannian manifoldsIn mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
for generalizations of Gauss curvature to higher-dimensional Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. - Curvature vector and geodesic curvatureGeodesic curvatureIn Riemannian geometry, the geodesic curvature k_g of a curve lying on a submanifold of the ambient space measures how far the curve is from being a geodesic...
for appropriate notions of curvature of curves in Riemannian manifolds, of any dimension. - CurveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
. - Degree of curvatureDegree of curvatureDegree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying....
. - Differential geometry of curvesDifferential geometry of curvesDifferential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
for a full treatment of curves embedded in a Euclidean space of arbitrary dimension. - DioptreDioptreA dioptre, or diopter, is a unit of measurement of the optical power of a lens or curved mirror, which is equal to the reciprocal of the focal length measured in metres . It is thus a unit of reciprocal length. For example, a 3-dioptre lens brings parallel rays of light to focus at metre...
a measurement of curvature used in optics. - Gauss-Bonnet theorem for an elementary application of curvature.
- Gauss mapGauss mapIn differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
for more geometric properties of Gauss curvature. - Hertz's principle of least curvature an expression of the Principle of Least ActionPrinciple of least actionIn physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
. - Mean curvatureMean curvatureIn mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
at one point on a surface. - Minimum railway curve radiusMinimum railway curve radiusThe minimum railway curve radius, the shortest design radius, has an important bearing on constructions costs and operating costs and, in combination with superelevation in the case of train tracks, determines the maximum safe speed of a curve. Superelevation is not a factor on tramway tracks...
. - Radius of curvatureRadius of curvatureThe distance from the center of a circle or sphere to its surface is its radius. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point....
. - Second fundamental form for the extrinsic curvature of hypersurfaces in general.