
Open set
Encyclopedia

Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, without explicitly having a concept of distance
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
defined. Concepts that use notions of nearness, such as the continuity of functions
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, can be translated into the language of open sets.
In point-set topology, open sets are used to distinguish between points
Topological indistinguishability
In topology, two points of a topological space X are topologically indistinguishable if they have exactly the same neighborhoods. That is, if x and y are points in X, and A is the set of all neighborhoods that contain x, and B is the set of all neighborhoods that contain y, then x and y are...
and subsets of a space. The degree to which any two points can be separated is specified by the separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s. The collection of all open sets in a space defines the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the space. Functions from one topological space to another that preserve the topology are the continuous functions. Although open sets and the topologies that they comprise are of central importance in point-set topology, they are also used as an organizational tool in other important branches of mathematics. Examples of topologies include the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
that reflects the algebraic nature of varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, and the topology on a differential manifold in differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
where each point within the space is contained in an open set that is homeomorphic to an open ball in a finite-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Point-set topology is the area of mathematics concerned with general topological spaces, and the relations between them. In the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of topological spaces, morphisms are continuous functions between topological spaces. Continuous functions are readily observed to preserve topological structure, as they map "points close together" to "points close together"; that is, they preserve the structure of open sets defined on the space.
In metric topology, one can concretely define a distance function between two points, and thus metric spaces also have a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, i.e. a certain structure of open sets defined on them. Thus, as opposed to the pure topological invariants, metric topology deals with isometries and the like; that is, distance preserving maps. In this case, the idea of an open set is used as an organizational tool rather than an object of study. From the topological point of view, metric spaces are fairly well understood, although many open problems still remain in metrizability theory.
Motivation
Intuitively, an open set provides a method to distinguish two points. For example, if about one point in a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
there exists an open set not containing another (distinct) point, the two points are referred to as topologically distinguishable. In this manner, one may speak of whether two subsets of a topological space are "near" without concretely defining a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the topological space. Therefore, topological spaces may be seen as a generalization of metric spaces.
In the set of all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, one has the natural Euclidean metric; that is, a function which measures the distance between two real numbers: d(x, y) = |x - y|. Therefore, given a real number, one can speak of the set of all points close to that real number; that is, within ε of that real number (refer to this real number as x). In essence, points within ε of x approximate x to an accuracy of degree ε. Note that ε > 0 always but as ε becomes smaller and smaller, one obtains points that approximate x to a higher and higher degree of accuracy. For example, if x = 0 and ε = 1, the points within ε of x are precisely the points of the interval (-1, 1); that is, the set of all real numbers between -1 and 1. However, with ε = 0.5, the points within ε of x are precisely the points of (-0.5, 0.5). Clearly, these points approximate x to a greater degree of accuracy compared to when ε = 1.
The previous discussion shows, for the case x = 0, that one may approximate x to higher and higher degrees of accuracy by defining ε to be smaller and smaller. In particular sets of the form (-ε, ε) give us a lot of information about points close to x = 0. Thus, rather than speaking of a concrete Euclidean metric, one may use sets to describe points close to x. This innovative idea has far-reaching consequences; in particular, by defining different collections of sets containing 0 (distinct from the sets (-ε, ε)), one may find different results regarding the distance between 0 and other real numbers. For example, if we were to define R as the only such set for "measuring distance", all points are close to 0 since there is only one possible degree of accuracy one may achieve in approximating 0: being a member of R. Thus, we find that in some sense, every real number is distance 0 away from 0! It may help in this case to think of the measure as being a binary condition, all things in R are equally close to 0, while any item that is not in R is not close to 0.
In general, one refers to the family of sets containing 0, used to approximate 0, as a neighborhood basis; a member of this neighborhood basis is referred to as an open set. In fact, one may generalize these notions to an arbitrary set (X); rather than just the real numbers. In this case, given a point (x) of that set, one may define a collection of sets "around" (that is, containing) x, used to approximate x. Of course, this collection would have to satisfy certain properties (known as axioms) for otherwise we may not have a well-defined method to measure distance. For example, every point in X should approximate x to some degree of accuracy. Thus X should be in this family. Once we begin to define "smaller" sets containing x, we tend to approximate x to a greater degree of accuracy. Bearing this in mind, one may define the remaining axioms that the family of sets about x is required to satisfy.
Definitions
The concept of open sets can be formalized with various degrees of generality, for example:Euclidean space
A subset U of the Euclidean n-spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is called open if, given any point x in U, there exists a real number ε > 0 such that, given any point y in Rn whose Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
from x is smaller than ε, y also belongs to U. Equivalently, a subset U of Rn is open if every point in U has a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
in Rn contained in U.
Metric spaces
A subset U of a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is called open if, given any point x in U, there exists a real number ε > 0 such that, given any point y in M with y also belongs to U. Equivalently, U is open if every point in U has a neighbourhood contained in U.
This generalises the Euclidean space example, since Euclidean space with the Euclidean distance is a metric space.
Topological spaces
If a nonempty set X is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
T, then any member of T is an open set.
Note that infinite intersections of open sets need not be open. For example, the intersection of all intervals of the form where n is a positive integer, is the set {0} which is not open in the real line. Sets that can be constructed as the intersection of countably many open sets are denoted Gδ
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
sets.
The topological definition of open sets generalises the metric space definition: If one begins with a metric space and defines open sets as before, then the family of all open sets is a topology on the metric space. Every metric space is therefore, in a natural way, a topological space. There are, however, topological spaces that are not metric spaces.
Properties
- The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is both open and closed (clopen setClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
). - The set X that the topology is defined on is both open and closed (clopen setClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
). - The unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of any number of open sets is open. - The intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of a finite number of open sets is open.
Uses
Open sets have a fundamental importance in topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. The concept is required to define and make sense of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and other topological structures that deal with the notions of closeness and convergence for spaces such as metric spaces and uniform spaces.
Every subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
A of a topological space X contains a (possibly empty) open set; the largest such open set is called the interior of A.
It can be constructed by taking the union of all the open sets contained in A.
Given topological spaces X and Y, a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f from X to Y is continuous if the preimage of every open set in Y is open in X.
The function f is called open if the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of every open set in X is open in Y.
An open set on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
has the characteristic property that it is a countable union of disjoint open intervals.
"Open" is defined relative to a particular topology
Whether a set is open depends on the topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
under consideration. Having opted for greater brevity over greater clarity, we refer to a set X endowed with a topology T as "the topological space X" rather than "the topological space (X, T)", despite the fact that all the topological data is contained in T. If there are two topologies on the same set, a set U that is open in the first topology might fail to be open in the second topology. For example, if X is any topological space and Y is any subset of X, the set Y can be given its own topology (called the 'subspace topology') defined by "A set U is open in the subspace topology on Y if and only if U is the intersection of Y with an open set from the original topology on X." This potentially introduces new open sets: if V is open in the original topology on X, but
 isn't, then
isn't, then  is open in the subspace topology on Y but not in the original topology on X.
is open in the subspace topology on Y but not in the original topology on X.As a concrete example of this, if U is defined as the set of rational numbers in the interval then U is an open subset of the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, but not of the real numbers. This is because when the surrounding space is the rational numbers, for every point x in U, there exists a positive number a such that all rational points within distance a of x are also in U. On the other hand, when the surrounding space is the reals, then for every point x in U there is no positive a such that all real points within distance a of x are in U (since U contains no non-rational numbers).
Open and closed are not mutually exclusive
A set might be open, closed, both, or neither.For example, we'll use the real line with its usual topology (the Euclidean topology
Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
), which is defined as follows: every interval (a,b) of real numbers belongs to the topology, and every union of such intervals, e.g.
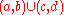 , belongs to the topology.
, belongs to the topology.- In any topology, the entire set X is declared open by definition, as is the empty set. Moreover, the complement of the entire set X is the empty set; since X has an open complement, this means by definition that X is closed. Hence, in any topology, the entire space is simultaneously open and closed ("clopenClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
"). - The interval
 is open because it belongs to the Euclidean topology. If I were to have an open complement, it would mean by definition that I were closed. But I does not have an open complement; its complement is
is open because it belongs to the Euclidean topology. If I were to have an open complement, it would mean by definition that I were closed. But I does not have an open complement; its complement is  , which does not belong to the Euclidean topology since it is not a union of intervals of the form
, which does not belong to the Euclidean topology since it is not a union of intervals of the form  . Hence, I is an example of a set that is open but not closed.
. Hence, I is an example of a set that is open but not closed. - By a similar argument, the interval
 is closed but not open.
is closed but not open. - Finally, since neither
 nor its complement
nor its complement 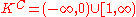 belongs to the Euclidean topology (neither one can be written as a union of intervals of the form (a,b) ), this means that K is neither open nor closed.
belongs to the Euclidean topology (neither one can be written as a union of intervals of the form (a,b) ), this means that K is neither open nor closed.

