
Subspace topology
Encyclopedia
In topology
and related areas of mathematics
, a subspace of a topological space
X is a subset
S of X which is equipped with a natural topology induced from that of X called the subspace topology (or the relative topology, or the induced topology, or the trace topology).
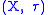 and a subset
and a subset
 of
of  , the subspace topology on
, the subspace topology on 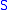 is defined by
is defined by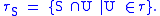
That is, a subset of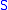 is open in the subspace topology if and only if
is open in the subspace topology if and only if
it is the intersection
of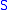 with an open set
with an open set
in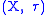 . If
. If 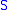 is equipped with the subspace topology then it is a topological space in its own right, and is called a subspace of
is equipped with the subspace topology then it is a topological space in its own right, and is called a subspace of 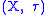 . Subsets of topological spaces are usually assumed to be equipped with the subspace topology unless otherwise stated.
. Subsets of topological spaces are usually assumed to be equipped with the subspace topology unless otherwise stated.
Alternatively we can define the subspace topology for a subset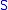 of
of  as the coarsest topology for which the inclusion map
as the coarsest topology for which the inclusion map

is continuous.
More generally, suppose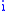 is an injection
is an injection
from a set to a topological space
to a topological space  . Then the subspace topology on
. Then the subspace topology on 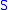 is defined as the coarsest topology for which
is defined as the coarsest topology for which 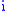 is continuous. The open sets in this topology are precisely the ones of the form
is continuous. The open sets in this topology are precisely the ones of the form 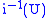 for
for  open in
open in  .
. 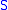 is then homeomorphic to its image in
is then homeomorphic to its image in  (also with the subspace topology) and
(also with the subspace topology) and 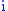 is called a topological embedding.
is called a topological embedding.
s with their usual topology.
 be a subspace of
be a subspace of  and let
and let  be the inclusion map. Then for any topological space
be the inclusion map. Then for any topological space  a map
a map  is continuous if and only if
is continuous if and only if
the composite map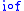 is continuous.
is continuous.
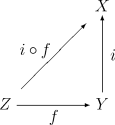 This property is characteristic in the sense that it can be used to define the subspace topology on
This property is characteristic in the sense that it can be used to define the subspace topology on  .
.
We list some further properties of the subspace topology. In the following let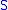 be a subspace of
be a subspace of  .
.
we have that all of its subspaces share the same property, then we say the topological property is hereditary. If only closed subspaces must share the property we call it weakly hereditary.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a subspace of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of X which is equipped with a natural topology induced from that of X called the subspace topology (or the relative topology, or the induced topology, or the trace topology).
Definition
Given a topological space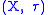 and a subset
and a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
 of
of  , the subspace topology on
, the subspace topology on 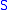 is defined by
is defined by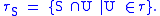
That is, a subset of
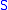 is open in the subspace topology if and only if
is open in the subspace topology if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of
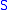 with an open set
with an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in
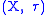 . If
. If 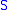 is equipped with the subspace topology then it is a topological space in its own right, and is called a subspace of
is equipped with the subspace topology then it is a topological space in its own right, and is called a subspace of 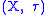 . Subsets of topological spaces are usually assumed to be equipped with the subspace topology unless otherwise stated.
. Subsets of topological spaces are usually assumed to be equipped with the subspace topology unless otherwise stated.Alternatively we can define the subspace topology for a subset
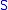 of
of  as the coarsest topology for which the inclusion map
as the coarsest topology for which the inclusion mapInclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....

is continuous.
More generally, suppose
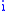 is an injection
is an injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from a set
 to a topological space
to a topological space  . Then the subspace topology on
. Then the subspace topology on 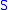 is defined as the coarsest topology for which
is defined as the coarsest topology for which 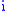 is continuous. The open sets in this topology are precisely the ones of the form
is continuous. The open sets in this topology are precisely the ones of the form 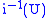 for
for  open in
open in  .
. 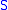 is then homeomorphic to its image in
is then homeomorphic to its image in  (also with the subspace topology) and
(also with the subspace topology) and 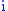 is called a topological embedding.
is called a topological embedding.Examples
In the following, R represents the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with their usual topology.
- The subspace topology of the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, as a subspace of R, is the discrete topology. - The rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q considered as a subspace of R do not have the discrete topology (the point 0 for example is not an open set in Q). If a and b are rational, then the intervals (a, b) and [a, b] are respectively open and closed, but if a and b are irrational, then the set of all x with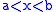 is both open and closed.
is both open and closed. - The set [0,1] as a subspace of R is both open and closed, whereas as a subset of R it is only closed.
- As a subspace of R,
 is composed of two disjoint open subsets (which happen also to be closed), and is therefore a disconnected space.
is composed of two disjoint open subsets (which happen also to be closed), and is therefore a disconnected space. - Let S = [0,1) be a subspace of the real line R. Then [0,½) is open in S but not in R. Likewise [½, 1) is closed in S but not in R. S is both open and closed as a subset of itself but not as a subset of R.
Properties
The subspace topology has the following characteristic property. Let be a subspace of
be a subspace of  and let
and let  be the inclusion map. Then for any topological space
be the inclusion map. Then for any topological space  a map
a map  is continuous if and only if
is continuous if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the composite map
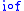 is continuous.
is continuous.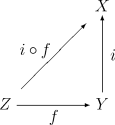
 .
.We list some further properties of the subspace topology. In the following let
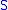 be a subspace of
be a subspace of  .
.- If
 is continuous the restriction to
is continuous the restriction to  is continuous.
is continuous. - If
 is continuous then
is continuous then  is continuous.
is continuous. - The closed sets in
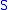 are precisely the intersections of
are precisely the intersections of 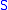 with closed sets in
with closed sets in  .
. - If
 is a subspace of
is a subspace of 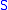 then
then  is also a subspace of
is also a subspace of  with the same topology. In other words the subspace topology that
with the same topology. In other words the subspace topology that  inherits from
inherits from 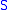 is the same as the one it inherits from
is the same as the one it inherits from  .
. - Suppose
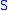 is an open subspace of
is an open subspace of  . Then a subspace of
. Then a subspace of  is open in
is open in 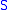 if and only if it is open in
if and only if it is open in  .
. - Suppose
 is a closed subspace of
is a closed subspace of  . Then a subspace of
. Then a subspace of 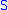 is closed in
is closed in 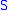 if and only if it is closed in
if and only if it is closed in  .
. - If
 is a base for
is a base for  then
then  is a basis for
is a basis for 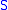 .
. - The topology induced on a subset of a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
by restricting the metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
to this subset coincides with subspace topology for this subset.
Preservation of topological properties
If whenever a topological space has a certain topological propertyTopological property
In topology and related areas of mathematics a topological property or topological invariant is a property of a topological space which is invariant under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic...
we have that all of its subspaces share the same property, then we say the topological property is hereditary. If only closed subspaces must share the property we call it weakly hereditary.
- Every open and every closed subspace of a topologically complete space is topologically complete.
- Every open subspace of a Baire spaceBaire spaceIn mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
is a Baire space. - Every closed subspace of a compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is compact. - Being a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is hereditary. - Being a normal spaceNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
is weakly hereditary. - Total boundedness is hereditary.
- Being totally disconnected is hereditary.
- First countability and second countability are hereditary.

