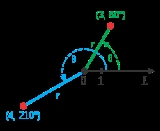
|
|
|
|
Polar coordinate system
|
| |
|
| |
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by an angle and a distance. The polar coordinate system is especially useful in situations where the relationship between two points is most easily expressed in terms of angles and distance; in the more familiar Cartesian or rectangular coordinate system, such a relationship can only be found through trigonometric formulation.
As the coordinate system is two-dimensional, each point is determined by two polar coordinates: the radial coordinate and the angular coordinate.
Discussion
Ask a question about 'Polar coordinate system' Start a new discussion about 'Polar coordinate system' Answer questions from other users |
Recent Posts
Encyclopedia
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by an angle and a distance. The polar coordinate system is especially useful in situations where the relationship between two points is most easily expressed in terms of angles and distance; in the more familiar Cartesian or rectangular coordinate system, such a relationship can only be found through trigonometric formulation.
As the coordinate system is two-dimensional, each point is determined by two polar coordinates: the radial coordinate and the angular coordinate. The radial coordinate (usually denoted as r ) denotes the point's distance from a central point known as the pole (equivalent to the origin in the Cartesian system). The angular coordinate (also known as the polar angle or the azimuth angle, and usually denoted by ? or t ) denotes the positive or anticlockwise (counterclockwise) angle required to reach the point from the 0° ray or polar axis (which is equivalent to the positive x-axis in the Cartesian coordinate plane).
History
The concepts of angle and radius were already used by ancient peoples of the 1st millennium BCE. The astronomer Hipparchus (190-120 BCE) created a table of chord functions giving the length of the chord for each angle, and there are references to his using polar coordinates in establishing stellar positions.
In On Spirals, Archimedes describes the Archimedean spiral, a function whose radius depends on the angle. The Greek work, however, did not extend to a full coordinate system.
In the 9th century CE, the Persian mathematician, Habash al-Hasib al-Marwazi, employed spherical trigonometry and map projection methods in order to convert polar coordinates to a different coordinate system centred on a specific point on the sphere, in this the Qibla, the direction to Mecca. The Persian geographer, Abu Rayhan Biruni (973-1048), developed ideas which are seen as an anticipation of the polar coordinate system. Around 1025 CE, he was the first to describe a polar equi-azimuthal equidistant projection of the celestial sphere.
There are various accounts of the introduction of polar coordinates as part of a formal coordinate system. The full history of the subject is described in Harvard professor Julian Lowell Coolidge's Origin of Polar Coordinates. Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-seventeenth century. Saint-Vincent wrote about them privately in 1625 and published his work in 1647, while Cavalieri published his in 1635 with a corrected version appearing in 1653. Cavalieri first used polar coordinates to solve a problem relating to the area within an Archimedean spiral. Blaise Pascal subsequently used polar coordinates to calculate the length of parabolic arcs.
In Method of Fluxions (written 1671, published 1736), Sir Isaac Newton examined the transformations between polar coordinates, which he referred to as the "Seventh Manner; For Spirals", and nine other coordinate systems. In the journal Acta Eruditorum (1691), Jacob Bernoulli used a system with a point on a line, called the pole and polar axis respectively. Coordinates were specified by the distance from the pole and the angle from the polar axis. Bernoulli's work extended to finding the radius of curvature of curves expressed in these coordinates.
The actual term polar coordinates has been attributed to Gregorio Fontana and was used by 18th-century Italian writers. The term appeared in English in George Peacock's 1816 translation of Lacroix's Differential and Integral Calculus. Alexis Clairaut was the first to think of polar coordinates in three dimensions, and Leonhard Euler was the first to actually develop them.
Plotting points with polar coordinates
Each point in the polar coordinate system can be described with the two polar coordinates, which are usually called r (the radial coordinate) and ? (the angular coordinate, polar angle, or azimuth angle, sometimes represented as f or t ). The r coordinate represents the radial distance from the pole, and the ? coordinate represents the anticlockwise (counterclockwise) angle from the 0° ray (sometimes called the polar axis), known as the positive x-axis on the Cartesian coordinate plane.
For example, the polar coordinates (3, 60°) would be plotted as a point 3 units from the pole on the 60° ray. The coordinates (−3, 240°) would also be plotted at this point because a negative radial distance is measured as a positive distance on the opposite ray (the ray reflected about the origin, which differs from the original ray by 180°).
One important aspect of the polar coordinate system, not present in the Cartesian coordinate system, is that a single point can be expressed with an infinite number of different coordinates. This is because any number of multiple revolutions can be made around the central pole without affecting the actual location of the point plotted. In general, the point (r, ?) can be represented as or , where n is any integer.
The arbitrary coordinates (0, ?) are conventionally used to represent the pole, as regardless of the ? coordinate, a point with radius 0 will always be on the pole. To get a unique representation of a point, it is usual to limit r to non-negative numbers and ? to the interval [0, 360°) or (-180°, 180°] (or, in radian measure, [0, 2p) or (-p, p]).
Angles in polar notation are generally expressed in either degrees or radians, using the conversion 2p rad = 360°. The choice depends largely on the context. Navigation applications use degree measure, while some physics applications (specifically rotational mechanics) and almost all mathematical literature on calculus use radian measure.
Converting between polar and Cartesian coordinates
The two polar coordinates r and ? can be converted to the Cartesian coordinates x and y by using the trigonometric functions sine and cosine:
while the two Cartesian coordinates x and y can be converted to polar coordinate r by
(by a simple application of the Pythagorean theorem).
To determine the angular coordinate ?, the following two ideas must be considered:
- For , ? can be set to any real value.
- For , to get a unique representation for ?, it must be limited to an interval of size 2p. Conventional choices for such an interval are [0, 2p) and (−p, p].
To obtain ? in the interval [0, 2p), the following may be used ( denotes the inverse of the tangent function):
To obtain ? in the interval (−p, p], the following may be used:
Many modern programming languages avoid having to keep track of the numerator and denominator signs through the implementation of the atan2 function, which has separate arguments for the numerator and the denominator. In languages which permit optional arguments, the atan function may also optionally be given the x coordinate (such as in Common Lisp).
Polar equations
The equation defining an algebraic curve expressed in polar coordinates is known as a polar equation. In many cases, such an equation can simply be specified by defining r as a function of ?. The resulting curve then consists of points of the form (r(?), ?) and can be regarded as the graph of the polar function r.
Different forms of symmetry can be deduced from the equation of a polar function r. If the curve will be symmetrical about the horizontal (0°/180°) ray, if it will be symmetric about the vertical (90°/270°) ray, and if it will be rotationally symmetric a° counterclockwise about the pole.
Because of the circular nature of the polar coordinate system, many curves can be described by a rather simple polar equation, whereas their Cartesian form is much more intricate. Among the best known of these curves are the polar rose, Archimedean spiral, lemniscate, limaçon, and cardioid.
For the circle, line, and polar rose below, it is understood that there are no restrictions on the domain and range of the curve.
Circle
The general equation for a circle with a center at and radius a is
This can be simplified in various ways, to conform to more specific cases, such as the equation
for a circle with a center at the pole and radius a.
Line
Radial lines (those running through the pole) are represented by the equation
,
where f is the angle of elevation of the line; that is, where m is the slope of the line in the Cartesian coordinate system. The non-radial line that crosses the radial line perpendicularly at the point (r0, f) has the equation
Polar rose
A polar rose is a famous mathematical curve that looks like a petalled flower, and that can be expressed as a simple polar equation,
for any constant (including 0). If k is an integer, these equations will produce a k-petalled rose if k is odd, or a 2k-petalled rose if k is even. If k is rational but not an integer, a rose-like shape may form but with overlapping petals. Note that these equations never define a rose with 2, 6, 10, 14, etc. petals. The variable a represents the length of the petals of the rose.
Archimedean spiral
The Archimedean spiral is a famous spiral that was discovered by Archimedes, which also can be expressed as a simple polar equation. It is represented by the equation
Changing the parameter a will turn the spiral, while b controls the distance between the arms, which for a given spiral is always constant. The Archimedean spiral has two arms, one for and one for . The two arms are smoothly connected at the pole. Taking the mirror image of one arm across the 90°/270° line will yield the other arm. This curve is notable as one of the first curves, after the conic sections, to be described in a mathematical treatise, and as being a prime example of a curve that is best defined by a polar equation.
Conic sections
A conic section with one focus on the pole and the other somewhere on the 0° ray (so that the conic's major axis lies along the polar axis) is given by:
-
where e is the eccentricity and is the semi-latus rectum (the perpendicular distance at a focus from the major axis to the curve). If , this equation defines a hyperbola; if , it defines a parabola; and if , it defines an ellipse. The special case of the latter results in a circle of radius .
Complex numbers
Every complex number can be represented as a point in the complex plane, and can therefore be expressed by specifying either the point's Cartesian coordinates (called rectangular or Cartesian form) or the point's polar coordinates (called polar form). The complex number z can be represented in rectangular form as
-
where i is the imaginary unit, or can alternatively be written in polar form (via the conversion formulae given above) as
and from there as
-
where e is Euler's number, which are equivalent as shown by Euler's formula. (Note that this formula, like all those involving exponentials of angles, assumes that the angle ? is expressed in radians.) To convert between the rectangular and polar forms of a complex number, the conversion formulae given above can be used.
For the operations of multiplication, division, and exponentiation of complex numbers, it is generally much simpler to work with complex numbers expressed in polar form rather than rectangular form. From the laws of exponentiation:
Calculus
Calculus can be applied to equations expressed in polar coordinates.
The angular coordinate ? is expressed in radians throughout this section, which is the conventional choice when doing calculus.
Differential calculus
We have the following formulas:
To find the Cartesian slope of the tangent line to a polar curve r(?) at any given point, the curve is first expressed as a system of parametric equations.
Differentiating both equations with respect to ? yields
Dividing the second equation by the first yields the Cartesian slope of the tangent line to the curve at the point (r, r(?)):
Integral calculus
Let R denote the region enclosed by a curve r(?) and the rays ? = a and ? = b, where . Then, the area of R is
This result can be found as follows. First, the interval is divided into n subintervals, where n is an arbitrary positive integer. Thus ??, the length of each subinterval, is equal to (the total length of the interval), divided by n, the number of subintervals. For each subinterval i = 1, 2, …, n, let ?i be the midpoint of the subinterval, and construct a sector with the center at the pole, radius r(?i ), central angle ?? and arc length r(?i )??. The area of each constructed sector is therefore equal to ½r(?i )2??. Hence, the total area of all of the sectors is
As the number of subintervals n is increased, the approximation of the area continues to improve. In the limit as n ? 8, the sum becomes the Riemann sum for the above integral.
Generalization
Using Cartesian coordinates, an infinitesimal area element can be calculated as dA = dx dy. The substitution rule for multiple integrals states that, when using other coordinates, the Jacobian determinant of the coordinate conversion formula has to be considered:
-
Hence, an area element in polar coordinates can be written as
Now, a function that is given in polar coordinates can be integrated as follows:
Here, R is the same region as above, namely, the region enclosed by a curve r(?) and the rays ? = a and ? = b.
The formula for the area of R mentioned above is retrieved by taking f identically equal to 1. A more surprising application of this result yields the Gaussian integral
Vector calculus
Vector calculus can also be applied to polar coordinates. Let be the position vector , with r and ? depending on time t.
Using the unit vectors
in the direction of and
at right angle to the first and second derivatives of position are:
Centrifugal and Coriolis terms
The term is sometimes referred to as the centrifugal term, and the term as the Coriolis term. For example, see Shankar. Although these equations bear some resemblance in form to the centrifugal and Coriolis effects found in rotating reference frames, nonetheless there is not a necessary physical connection. For example, the physical centrifugal and Coriolis forces appear only in non-inertial frames of reference. In contrast, these terms that appear when acceleration is expressed in polar coordinates are a mathematical consequence of differentiation; these terms appear wherever polar coordinates are used. In particular, these terms appear even when polar coordinates are used in inertial frames of reference, where the physical centrifugal and Coriolis forces never appear.
Co-rotating frame
For a particle in planar motion, one approach to attaching physical significance to these terms is based on the concept of an instantaneous co-rotating frame of reference. To define a co-rotating frame, first an origin is selected from which the distance r(t) to the particle is defined. An axis of rotation is set up that is perpendicular to the plane of motion of the particle, and passing through this origin. Then, at the selected moment t, the rate of rotation of the co-rotating frame O is made to match the rate of rotation of the particle about this axis, d?/dt. Next, the terms in the acceleration in the inertial frame are related to those in the co-rotating frame. Let the location of the particle in the inertial frame be (r(t), ?(t)), and in the co-rotating frame be (r(t), ?'(t)). Because the co-rotating frame rotates at the same rate as the particle, d?'/dt = 0. The fictitious centrifugal force in in co-rotating frame is mrO2, radially outward. The velocity of the particle in the co-rotating frame also is radially outward, because d?'/dt = 0, and has a value -2m(dr/dt)O, pointed in the direction of ?. Thus, using these forces in Newton's second law we find:
where over dots represent time differentiations, and F is the net real force (as opposed to the fictitious forces). In terms of components, this vector equation becomes:
which can be compared to the equations for the inertial frame:
This comparison, plus the recognition that by the definition of the co-rotating frame at time t it has a rate of rotation O = d?/dt, shows that we can interpret the terms in the acceleration (multiplied by the mass of the particle) as found in the inertial frame as the negative of the centrifugal and Coriolis forces that would be seen in the instantaneous, non-inertial co-rotating frame.
For general motion of a particle (as opposed to simple circular motion), the centrifugal and Coriolis forces in a particle's frame of reference commonly are referred to the instantaneous osculating circle of its motion, not to a fixed center of polar coordinates. For more detail, see centripetal force.
Three dimensions
The polar coordinate system is extended into three dimensions with two different coordinate systems, the cylindrical and spherical coordinate systems, both of which include two-dimensional or planar polar coordinates as a subset. In essence, the cylindrical coordinate system extends polar coordinates by adding an additional distance coordinate, while the spherical system instead adds an additional angular coordinate.
Cylindrical coordinates
The cylindrical coordinate system is a coordinate system that essentially extends the two-dimensional polar coordinate system by adding a third coordinate measuring the height of a point above the plane, similar to the way in which the Cartesian coordinate system is extended into three dimensions. The third coordinate is usually denoted h, making the three cylindrical coordinates (r, ?, h).
The three cylindrical coordinates can be converted to Cartesian coordinates by
Spherical coordinates
Polar coordinates can also be extended into three dimensions using the coordinates (?, f, ?), where ? is the distance from the origin, f is the angle from the z-axis (called the colatitude or zenith and measured from 0 to 180°) and ? is the angle from the x-axis (as in the polar coordinates). This coordinate system, called the spherical coordinate system, is similar to the latitude and longitude system used for Earth, with the origin in the centre of Earth, the latitude d being the complement of f, determined by d = 90° - f, and the longitude l being measured by l = ? - 180°.
The three spherical coordinates are converted to Cartesian coordinates by
Applications
Polar coordinates are two-dimensional and thus they can be used only where point positions lie on a single two-dimensional plane. They are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point. For instance, the examples above show how elementary polar equations suffice to define curves — such as the Archimedean spiral — whose equation in the Cartesian coordinate system would be much more intricate. Moreover, many physical systems — such as those concerned with bodies moving around a central point or with phenomena originating from a central point — are simpler and more intuitive to model using polar coordinates. The initial motivation for the introduction of the polar system was the study of circular and orbital motion.
Position and navigation
Polar coordinates are used often in navigation, as the destination or direction of travel can be given as an angle and distance from the object being considered. For instance, aircraft use a slightly modified version of the polar coordinates for navigation. In this system, the one generally used for any sort of navigation, the 0° ray is generally called heading 360, and the angles continue in a clockwise direction, rather than counterclockwise, as in the mathematical system. Heading 360 corresponds to magnetic north, while headings 90, 180, and 270 correspond to magnetic east, south, and west, respectively. Thus, an aircraft traveling 5 nautical miles due east will be traveling 5 units at heading 90 (read zero-niner-zero by air traffic control).
Modeling
Systems displaying radial symmetry provide natural settings for the polar coordinate system, with the central point acting as the pole. A prime example of this usage is the groundwater flow equation when applied to radially symmetric wells. Systems with a radial force are also good candidates for the use of the polar coordinate system. These systems include gravitational fields, which obey the inverse-square law, as well as systems with point sources, such as radio antennas.
Radially asymmetric systems may also be modeled with polar coordinates. For example, a microphone's pickup pattern illustrates its proportional response to an incoming sound from a given direction, and these patterns can be represented as polar curves. The curve for a standard cardioid microphone, the most common unidirectional microphone, can be represented as at its target design frequency. The pattern shifts toward omnidirectionality at lower frequencies.
Three dimensional modeling of loudspeaker output patterns can be used to predict their performance. A number of polar plots are required, taken at a wide selection of frequencies, as the pattern changes greatly with frequency. Polar plots help to show that many loudspeakers tend toward omnidirectionality at lower frequencies.
External links
See also
|
| |
|
|
