Diagonal matrix
Encyclopedia
In linear algebra
, a diagonal matrix is a matrix
(usually a square matrix) in which the entries outside the main diagonal (↘) are all zero. The diagonal entries themselves may or may not be zero. Thus, the matrix D = (di,j) with
n columns and n rows is diagonal if:
For example, the following matrix is diagonal: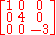
The term diagonal matrix may sometimes refer to a rectangular diagonal matrix, which is an m-by-n matrix with only the entries of the form di,i possibly non-zero. For example: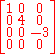
or 
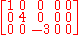
However, in the remainder of this article we will consider only square matrices. Any square diagonal matrix is also a symmetric matrix. Also, if the entries come from the field
R or C, then it is a normal matrix
as well. Equivalently, we can define a diagonal matrix as a matrix that is both upper-
and lower-triangular
. The identity matrix
In and any square zero matrix are diagonal. A one-dimensional matrix is always diagonal.
I. Its effect on a vector is scalar multiplication
by λ. For example, a 3×3 scalar matrix has the form: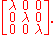
The scalar matrices are the center of the algebra of matrices: that is, they are precisely the matrices that commute with all other square matrices of the same size.
For an abstract vector space V (rather than the concrete vector space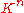
), or more generally a module M over a ring R, with the endomorphism algebra End(M) (algebra of linear operators on M) replacing the algebra of matrices, the analog of scalar matrices are scalar transformations. Formally, scalar multiplication is a linear map, inducing a map 
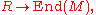(send a scalar λ to the corresponding scalar transformation, multiplication by λ) exhibiting End(M) as a R-algebra
. For vector spaces, or more generally free module
s
, for which the endomorphism algebra is isomorphic to a matrix algebra, the scalar transforms are exactly the center of the endomorphism algebra, and similarly invertible transforms are the center of the general linear group
GL(V), where they are denoted by Z(V), follow the usual notation for the center.
are especially simple for diagonal matrices. Write diag(a1,...,an) for a diagonal matrix whose diagonal entries starting in the upper left corner are a1,...,an. Then, for addition, we have
and for matrix multiplication
,
The diagonal matrix diag(a1,...,an) is invertible if and only if
the entries a1,...,an are all non-zero. In this case, we have
In particular, the diagonal matrices form a subring
of the ring of all n-by-n matrices.
Multiplying an n-by-n matrix A from the left with diag(a1,...,an) amounts to multiplying the i-th row of A by ai for all i; multiplying the matrix A from the right with diag(a1,...,an) amounts to multiplying the i-th column of A by ai for all i.
of diag(a1, ..., an) is the product a1...an.
The adjugate of a diagonal matrix is again diagonal.
A square matrix is diagonal if and only if it is triangular and normal
.
In fact, a given n-by-n matrix A is similar to a diagonal matrix (meaning that there is a matrix X such that X-1AX is diagonal) if and only if it has n linearly independent eigenvectors. Such matrices are said to be diagonalizable
.
Over the field
of real
or complex
numbers, more is true. The spectral theorem
says that every normal matrix
is unitarily similar to a diagonal matrix (if AA* = A*A then there exists a unitary matrix U such that UAU* is diagonal). Furthermore, the singular value decomposition
implies that for any matrix A, there exist unitary matrices U and V such that UAV* is diagonal with positive entries.
, particularly the study of PDEs
, operators are particularly easy to understand, and PDEs easy to solve, if the operator is diagonal with respect to the basis one is working with – this corresponds to a separable partial differential equation
. Thus, a key technique to understand operators is to have a change of coordinates – in the language of operators, an integral transform – which changes the basis to an eigenbasis of eigenfunction
s: which makes the equation separable. An important example of this is the Fourier transform
, which diagonalizes constant coefficient differentiation operators (or more generally translation invariant operators), such as the Laplacian operator, say, in the heat equation
.
Especially easy are multiplication operator
s, which are defined as multiplication by (the values of) a fixed function – the values of the function at each point correspond to the diagonal entries of a matrix.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a diagonal matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(usually a square matrix) in which the entries outside the main diagonal (↘) are all zero. The diagonal entries themselves may or may not be zero. Thus, the matrix D = (di,j) with
n columns and n rows is diagonal if:
For example, the following matrix is diagonal:
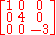
The term diagonal matrix may sometimes refer to a rectangular diagonal matrix, which is an m-by-n matrix with only the entries of the form di,i possibly non-zero. For example:
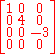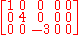
or However, in the remainder of this article we will consider only square matrices. Any square diagonal matrix is also a symmetric matrix. Also, if the entries come from the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
R or C, then it is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
as well. Equivalently, we can define a diagonal matrix as a matrix that is both upper-
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
and lower-triangular
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
. The identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
In and any square zero matrix are diagonal. A one-dimensional matrix is always diagonal.
Scalar matrix
A diagonal matrix with all its main diagonal entries equal is a scalar matrix, that is, a scalar multiple λI of the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
I. Its effect on a vector is scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by λ. For example, a 3×3 scalar matrix has the form:
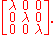
The scalar matrices are the center of the algebra of matrices: that is, they are precisely the matrices that commute with all other square matrices of the same size.
For an abstract vector space V (rather than the concrete vector space
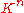), or more generally a module M over a ring R, with the endomorphism algebra End(M) (algebra of linear operators on M) replacing the algebra of matrices, the analog of scalar matrices are scalar transformations. Formally, scalar multiplication is a linear map, inducing a map 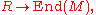(send a scalar λ to the corresponding scalar transformation, multiplication by λ) exhibiting End(M) as a R-algebraAlgebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
. For vector spaces, or more generally free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s
, for which the endomorphism algebra is isomorphic to a matrix algebra, the scalar transforms are exactly the center of the endomorphism algebra, and similarly invertible transforms are the center of the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(V), where they are denoted by Z(V), follow the usual notation for the center.
Matrix operations
The operations of matrix addition and matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
are especially simple for diagonal matrices. Write diag(a1,...,an) for a diagonal matrix whose diagonal entries starting in the upper left corner are a1,...,an. Then, for addition, we have
- diag(a1,...,an) + diag(b1,...,bn) = diag(a1+b1,...,an+bn)
and for matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
,
- diag(a1,...,an) · diag(b1,...,bn) = diag(a1b1,...,anbn).
The diagonal matrix diag(a1,...,an) is invertible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the entries a1,...,an are all non-zero. In this case, we have
- diag(a1,...,an)-1 = diag(a1-1,...,an-1).
In particular, the diagonal matrices form a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of the ring of all n-by-n matrices.
Multiplying an n-by-n matrix A from the left with diag(a1,...,an) amounts to multiplying the i-th row of A by ai for all i; multiplying the matrix A from the right with diag(a1,...,an) amounts to multiplying the i-th column of A by ai for all i.
Other properties
The eigenvalues of diag(a1, ..., an) are a1, ..., an with associated eigenvectors of e1, ..., en, where the vector ei is all zeros except a one in the ith row. The determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of diag(a1, ..., an) is the product a1...an.
The adjugate of a diagonal matrix is again diagonal.
A square matrix is diagonal if and only if it is triangular and normal
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
.
Uses
Diagonal matrices occur in many areas of linear algebra. Because of the simple description of the matrix operation and eigenvalues/eigenvectors given above, it is always desirable to represent a given matrix or linear map by a diagonal matrix.In fact, a given n-by-n matrix A is similar to a diagonal matrix (meaning that there is a matrix X such that X-1AX is diagonal) if and only if it has n linearly independent eigenvectors. Such matrices are said to be diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
.
Over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers, more is true. The spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
says that every normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
is unitarily similar to a diagonal matrix (if AA* = A*A then there exists a unitary matrix U such that UAU* is diagonal). Furthermore, the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
implies that for any matrix A, there exist unitary matrices U and V such that UAV* is diagonal with positive entries.
Operator theory
In operator theoryOperator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, particularly the study of PDEs
PDES
PDES may refer to:*Process Development Execution System -- systems supporting the execution of high-tech manufacturing process developments*ISO 10303*Partial differential equations...
, operators are particularly easy to understand, and PDEs easy to solve, if the operator is diagonal with respect to the basis one is working with – this corresponds to a separable partial differential equation
Separable partial differential equation
A separable partial differential equation is one that can be broken into a set of separate equations of lower dimensionality by a method of separation of variables. This generally relies upon the problem having some special form or symmetry...
. Thus, a key technique to understand operators is to have a change of coordinates – in the language of operators, an integral transform – which changes the basis to an eigenbasis of eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s: which makes the equation separable. An important example of this is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, which diagonalizes constant coefficient differentiation operators (or more generally translation invariant operators), such as the Laplacian operator, say, in the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
.
Especially easy are multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
s, which are defined as multiplication by (the values of) a fixed function – the values of the function at each point correspond to the diagonal entries of a matrix.
See also
- Anti-diagonal matrixAnti-diagonal matrixIn mathematics, an anti-diagonal matrix is a matrix where all the entries are zero except those on the diagonal going from the lower left corner to the upper right corner , known as the anti-diagonal....
- Banded matrix
- Bidiagonal matrixBidiagonal matrixA bidiagonal matrix is a matrix with non-zero entries along the main diagonal and either the diagonal above or the diagonal below.So that means there are two non zero diagonal in the matrix....
- Diagonally dominant matrixDiagonally dominant matrixIn mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other entries in that row...
- Diagonalizable matrixDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
- Multiplication operatorMultiplication operatorIn operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
- Tridiagonal matrix
- Toeplitz matrixToeplitz matrixIn linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
- Toral Lie algebraToral Lie algebraIn mathematics, a toral Lie algebra is a Lie subalgebra of a general linear Lie algebra all of whose elements are diagonalizable . Equivalently, a Lie algebra is toral if it contains no nonzero nilpotent elements...
- Circulant matrixCirculant matrixIn linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...