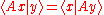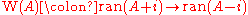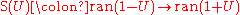Self-adjoint operator
Encyclopedia
In mathematics
, on a finite-dimensional inner product space
, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix
is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose
. By the finite-dimensional spectral theorem
such operators have an orthonormal basis
in which the operator can be represented as a diagonal matrix
with entries in the real number
s. In this article, we consider generalization
s of this concept
to operators on Hilbert space
s of arbitrary dimension.
Self-adjoint operators are used in functional analysis
and quantum mechanics
. In quantum mechanics their importance lies in the fact that in the Dirac
–von Neumann formulation of quantum mechanics, physical observable
s such as position, momentum
, angular momentum
and spin
are represented by self-adjoint operators on a Hilbert space. Of particular significance is the Hamiltonian
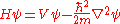
which as an observable corresponds to the total energy of a particle of mass m in a real potential field V. Differential operators are an important class of unbounded operator
s.
The structure of self-adjoint operators on infinite-dimensional Hilbert spaces essentially resembles the
finite-dimensional case, that is to say, operators are self-adjoint if and only if they are unitarily equivalent to real-valued multiplication operators. With suitable modifications, this result can be extended to possibly unbounded operators on infinite-dimensional spaces. Since an everywhere defined self-adjoint operator is necessarily bounded, one needs be more attentive to the domain issue in the unbounded case. This is explained below in more detail.
H is called symmetric if
for all elements x and y in the domain of A. More generally, a partially-defined linear operator A from a topological vector space
E into its continuous dual space E∗ is said to be symmetric if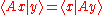
for all elements x and y in the domain of A. This usage is fairly standard in the functional analysis literature.
A symmetric everywhere defined operator is self-adjoint
.
By the Hellinger-Toeplitz theorem, a symmetric everywhere defined operator is bounded
.
Bounded symmetric operators are also called Hermitian.
The previous definition agrees with the one for matrices given in the introduction to this article, if we take as H the Hilbert space Cn with the standard dot product and interpret a square matrix as a linear operator on this Hilbert space. It is however much more general as there are important infinite-dimensional Hilbert spaces.
The spectrum of any bounded symmetric operator is real; in particular all its eigenvalues are real, although a symmetric operator may have no eigenvalues.
A general version of the spectral theorem
which also applies to bounded symmetric operators (see Read and Simon, vol. 1, chapter VII, or other books cited) is stated below. If the set of eigenvalues for a symmetric operator is non empty, and the eigenvalues are nondegenerate, then it follows from the definition that eigenvectors corresponding to distinct eigenvalues are orthogonal.
Contrary to what is sometimes claimed in introductory physics textbooks, it is possible for symmetric operators to have no eigenvalues at all (although the spectrum
of any self-adjoint operator is nonempty). The example below illustrates the special case when an (unbounded) symmetric operator does have a set of eigenvectors which constitute a Hilbert space basis. The operator A below can be seen to have a compact
inverse, meaning that the corresponding differential equation A f = g is solved by some integral, therefore compact, operator G. The compact symmetric operator G then has a countable family of eigenvectors which are complete in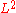 . The same can then be said for A.
. The same can then be said for A.
Example. Consider the complex Hilbert space L2[0,1] and the differential operator
defined on the subspace consisting of all complex-valued infinitely differentiable functions f on [0,1] with the boundary conditions:
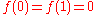
Then integration by parts
shows that A is symmetric. Its eigenfunctions are the sinusoids

with the real eigenvalues n2π2; the well-known orthogonality of the sine functions follows as a consequence of the property of being symmetric.
We consider generalizations of this operator below.
Notice that it is the denseness of the domain of the operator, along with the uniqueness part of Riesz representation, that ensures the adjoint operator is well defined.
A result of Hellinger-Toeplitz type says that an operator having an everywhere defined bounded adjoint is bounded.
The condition for a linear operator on a Hilbert space to be self-adjoint is stronger than to be symmetric.
For any densely defined operator A on Hilbert space one can define its adjoint operator A*.
For a symmetric operator A, the domain of the operator A* contains the domain of the operator A, and the restriction of the operator A* on the domain of A coincides with the operator A, i.e.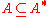 , in other words A* is extension of A. For a self-adjoint operator A the domain of A* is the same as the domain of A, and A=A*. See also Extensions of symmetric operators
, in other words A* is extension of A. For a self-adjoint operator A the domain of A* is the same as the domain of A, and A=A*. See also Extensions of symmetric operators
and unbounded operator
.

Theorem. Let J be the symplectic mapping
given by
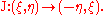
Then the graph of A* is the orthogonal complement of JG(A):
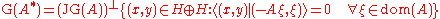
A densely defined operator A is symmetric if and only if
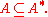
where the subset notation is understood to mean
is understood to mean 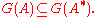 An operator A is self-adjoint if and only if
An operator A is self-adjoint if and only if 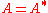 ; that is, if and only if
; that is, if and only if 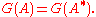
Example. Consider the complex Hilbert space L2(R), and the operator which multiplies a given function by x:
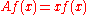
The domain of A is the space of all L2 functions for which the right-hand-side is square-integrable. A is a symmetric operator without any eigenvalues and eigenfunctions. In fact it turns out that the operator is self-adjoint, as follows from the theory outlined below.
As we will see later, self-adjoint operators have very important spectral properties; they are in fact multiplication operators on general measure spaces.
U:H → K such that
A multiplication operator
is defined as follows: Let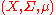 be a countably additive measure space and f a real-valued measurable function on X. An operator T of the form
be a countably additive measure space and f a real-valued measurable function on X. An operator T of the form
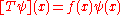
whose domain is the space of ψ for which the right-hand side above is in L2 is called a multiplication operator.
Theorem. Any multiplication operator is a (densely defined) self-adjoint operator. Any self-adjoint operator is unitarily equivalent to a multiplication operator.
This version of the spectral theorem for self-adjoint operators can be proved by reduction to the spectral theorem for unitary operators. This reduction uses the Cayley transform for self-adjoint operators which is defined in the next section. We might note that if T is multiplication by f, then the spectrum of T is just the essential range
of f.
: If h is a bounded real-valued Borel function on R, then h(T) is the operator of multiplication by the composition . In order for this to be well-defined, we must show that it is the unique operation on bounded real-valued Borel functions satisfying a number of conditions.
. In order for this to be well-defined, we must show that it is the unique operation on bounded real-valued Borel functions satisfying a number of conditions.
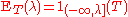
where denotes the function which is identically 1 on the interval
denotes the function which is identically 1 on the interval  . The family of projection operators ET(λ) is called resolution of the identity for T. Moreover, the following Stieltjes integral representation for T can be proved:
. The family of projection operators ET(λ) is called resolution of the identity for T. Moreover, the following Stieltjes integral representation for T can be proved:
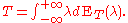
The definition of the operator integral above can be reduced to that that of a scalar valued Stieltjes integral using the weak operator topology. In more modern treatments however, this representation is usually avoided, since most technical problems can be dealt with by the functional calculus.
using Dirac notation as follows:
If H is Hermitian (the name for self-adjoint in the physics literature) and f is a Borel function,

with
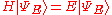
where the integral runs over the whole spectrum of H. The notation suggests that H is diagonalized by the eigenvalues ΨE. Such a notation is purely formal
. One can see the similarity between Dirac's notation and the previous section. The resolution of the identity (sometimes called projection valued measures) formally resembles the rank-1 projections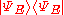 .
.
In the Dirac notation, (projective) measurements are described via eigenvalues and eigenstates, both purely formal objects. As one would expect, this does not survive passage to the resolution of the identity. In the latter formulation, measurements are described using the spectral measure of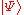 , if the system is prepared in
, if the system is prepared in 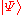 prior to the measurement. Alternatively, if one would like to preserve the notion of eigenstates and make it rigorous, rather than merely formal, one can replace the state space by a suitable rigged Hilbert space
prior to the measurement. Alternatively, if one would like to preserve the notion of eigenstates and make it rigorous, rather than merely formal, one can replace the state space by a suitable rigged Hilbert space
.
If f=1, the theorem is referred to as resolution of unity:

In the case is the sum of an Hermitian H and a skew-Hermitian (see skew-Hermitian matrix
is the sum of an Hermitian H and a skew-Hermitian (see skew-Hermitian matrix
) operator , one defines the biorthogonal basis set
, one defines the biorthogonal basis set
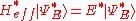
and write the spectral theorem as:

(See Feshbach–Fano partitioning method for the context where such operators appear in scattering theory
).
of a self-adjoint operator and the deficiency indices. (We should note here that it is often of technical convenience to deal with closed operator
s. In the symmetric case, the closedness requirement poses no obstacles, since it is known that all symmetric operators are closable.)
Theorem. Suppose A is a symmetric operator. Then there is a
unique partially defined linear operator
such that
Here, ran and dom denote the range
and the domain
, respectively. W(A) is isometric
on its domain. Moreover, the range of 1 − W(A) is dense
in H.
Conversely, given any partially defined operator U which is isometric on its domain (which is not
necessarily closed) and such that 1 − U is dense, there is a (unique) operator S(U)
such that
The operator S(U) is densely defined and symmetric.
The mappings W and S are inverses of each other.
The mapping W is called the Cayley transform. It associates a partially defined isometry
to any symmetric densely-defined operator. Note that the mappings W and S are : This means that if B is a symmetric operator that extends the densely defined symmetric operator A, then W(B) extends W(A), and similarly for S.
Theorem. A necessary and sufficient condition for A to be self-adjoint is that its Cayley transform W(A) be unitary.
This immediately gives us a necessary and sufficient condition for A to have a self-adjoint extension, as follows:
Theorem. A necessary and sufficient condition for A to have a self-adjoint extension is that W(A) have a unitary extension.
A partially defined isometric operator V on a Hilbert space H has a unique isometric extension to the norm closure of dom(V). A partially defined isometric operator with closed domain is called a partial isometry
.
Given a partial isometry V, the deficiency indices of V are defined as the dimension of the orthogonal complements of the domain and range:


Theorem. A partial isometry V has a unitary extension if and only if the deficiency indices are identical. Moreover, V has a unique unitary extension if and only if the both deficiency indices are zero.
We see that there is a bijection between symmetric extensions of an operator and isometric extensions of its Cayley transform. An operator which has a unique self-adjoint extension is said to be essentially self-adjoint. Such operators have a well-defined Borel functional calculus
. Symmetric operators which are not essentially self-adjoint may still have a canonical
self-adjoint extension. Such is the case for non-negative symmetric operators (or more generally, operators which are bounded below). These operators always have a canonically defined Friedrichs extension
and for these operators we can define a canonical functional calculus. Many operators that occur in analysis are bounded below (such as the negative of the Laplacian operator), so the issue of essential adjointness for these operators is less critical.
operators. However, many physical problems are formulated as a time-evolution equation involving differential operators for which the Hamiltonian is only symmetric. In such cases, either the Hamiltonian is essentially self-adjoint, in which case the physical problem has unique solutions or one attempts to find self-adjoint extensions of the Hamiltonian corresponding to different types of boundary conditions or conditions at infinity.
Example. The one-dimensional Schrödinger operator with the potential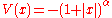 , defined initially on smooth compactly supported functions, is essentially self-adjoint (that is, has a self-adjoint closure) for
, defined initially on smooth compactly supported functions, is essentially self-adjoint (that is, has a self-adjoint closure) for  but not for
but not for  See Berezin and Schubin, page 55.
See Berezin and Schubin, page 55.
Example. There is no self-adjoint momentum operator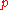 for a particle moving on a half-line. Nevertheless, the Hamiltonian
for a particle moving on a half-line. Nevertheless, the Hamiltonian 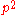 of a "free" particle on a half-line has several self-adjoint extensions corresponding to different types of boundary conditions. Physically, these boundary conditions are related to reflections of the particle at the origin (see Reed and Simon, vol.2).
of a "free" particle on a half-line has several self-adjoint extensions corresponding to different types of boundary conditions. Physically, these boundary conditions are related to reflections of the particle at the origin (see Reed and Simon, vol.2).
Theorem. Suppose A is a densely defined symmetric operator. Let

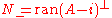
Then


and

where the decomposition is orthogonal relative to the graph inner product of dom(A*):
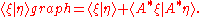
These are referred to as von Neumann's formulas in the Akhiezer and Glazman reference.
defined on the space of complex-valued C∞ functions on [0,1] vanishing near 0 and 1. D is a symmetric operator as can be shown by integration by parts
. The spaces N+, N− are given respectively by the distribution
al solutions to the equation


which are in L2 [0,1]. One can show that each one of these solution spaces is 1-dimensional, generated by the functions
x → eix and x → e−ix respectively. This shows that D is not essentially self-adjoint, but does have self-adjoint extensions. These self-adjoint extensions are parametrized by the space of unitary mappings
which in this case happens to be the unit circle T.
This simple example illustrates a general fact about self-adjoint extensions of symmetric differential operators P on an open set M. They are determined by the unitary maps between the eigenvalue spaces
where Pdist is the distributional extension of P.
We next give the example of differential operators with constant coefficients. Let
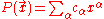
be a polynomial on Rn with real coefficients, where α ranges over a (finite) set of multi-indices. Thus
and
We also use the notation
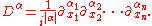
Then the operator P(D) defined on the space of infinitely differentiable functions of compact support on Rn by

is essentially self-adjoint on L2(Rn).
Theorem. Let P a polynomial function on Rn with real coefficients, F the Fourier transform considered as a unitary map L2(Rn) → L2(Rn). Then F* P(D) F is essentially self-adjoint and its unique self-adjoint extension is the operator of multiplication by the function P.
More generally, consider linear differential operators acting on infinitely differentiable complex-valued functions of compact support. If M is an open subset of Rn
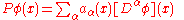
where aα are (not necessarily constant) infinitely differentiable functions. P is a linear operator
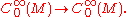
Corresponding to P there is another differential operator, the formal adjoint of P

Theorem. The operator theoretic adjoint P* of P is a restriction of the distributional extension of the formal adjoint. Specifically:
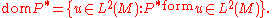
-Hellinger
theory of spectral multiplicity.
We first define uniform multiplicity:
Definition. A self-adjoint operator A has uniform multiplicity n where n is such that 1 ≤ n ≤ ω
if and only if A is unitarily equivalent to the operator Mf of multiplication by the function f(λ) = λ on

where Hn is a Hilbert space of dimension n. The domain of Mf consists of vector-valued functions ψ on R such that
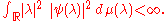
Non-negative countably additive measures μ, ν are mutually singular if and only if they are supported on disjoint Borel sets.
Theorem. Let A be a self-adjoint operator on a separable Hilbert space H. Then there is an ω sequence of countably additive finite measures on R (some of which may be identically 0)
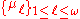
such that the measures are pairwise singular and A is unitarily equivalent to the operator of multiplication by the function f(λ) = λ on
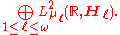
This representation is unique in the following sense: For any two such representations of the same A, the corresponding measures are equivalent in the sense that they have the same sets of measure 0.
The spectral multiplicity theorem can be reformulated using the language of direct integral
s of Hilbert spaces:
Theorem. Any self-adjoint operator on a separable Hilbert space is unitarily equivalent to multiplication by the function λ → λ on
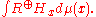
The measure equivalence class of μ (or equivalently its sets of measure 0) is uniquely determined and the measurable family
{Hx}x is determined almost everywhere with respect to μ.

As remarked above, the Laplacian is diagonalized by the Fourier transform. Actually it is more natural to consider the negative of the Laplacian - Δ since as an operator it is non-negative; (see elliptic operator
).
Theorem. If n=1, then -Δ has uniform multiplicity mult=2, otherwise -Δ has uniform multiplicity mult=ω. Moreover, the measure μmult is Borel measure on[ 0, ∞).
Example. The Hamiltonian for the harmonic oscillator has a quadratic potential V, that is

This Hamiltonian has pure point spectrum; this is typical for bound state Hamiltonians
in quantum mechanics. As was pointed out in a previous example, a sufficient condition that an unbounded symmetric operator has eigenvectors which form a Hilbert space basis is that it has a compact inverse.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, on a finite-dimensional inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. By the finite-dimensional spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
such operators have an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
in which the operator can be represented as a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
with entries in the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. In this article, we consider generalization
Generalization
A generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
s of this concept
Concept
The word concept is used in ordinary language as well as in almost all academic disciplines. Particularly in philosophy, psychology and cognitive sciences the term is much used and much discussed. WordNet defines concept: "conception, construct ". However, the meaning of the term concept is much...
to operators on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s of arbitrary dimension.
Self-adjoint operators are used in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. In quantum mechanics their importance lies in the fact that in the Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
–von Neumann formulation of quantum mechanics, physical observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s such as position, momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
are represented by self-adjoint operators on a Hilbert space. Of particular significance is the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
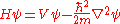
which as an observable corresponds to the total energy of a particle of mass m in a real potential field V. Differential operators are an important class of unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
s.
The structure of self-adjoint operators on infinite-dimensional Hilbert spaces essentially resembles the
finite-dimensional case, that is to say, operators are self-adjoint if and only if they are unitarily equivalent to real-valued multiplication operators. With suitable modifications, this result can be extended to possibly unbounded operators on infinite-dimensional spaces. Since an everywhere defined self-adjoint operator is necessarily bounded, one needs be more attentive to the domain issue in the unbounded case. This is explained below in more detail.
Symmetric operators
A partially-defined linear operator A on a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is called symmetric if
for all elements x and y in the domain of A. More generally, a partially-defined linear operator A from a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
E into its continuous dual space E∗ is said to be symmetric if
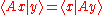
for all elements x and y in the domain of A. This usage is fairly standard in the functional analysis literature.
A symmetric everywhere defined operator is self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
.
By the Hellinger-Toeplitz theorem, a symmetric everywhere defined operator is bounded
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
.
Bounded symmetric operators are also called Hermitian.
The previous definition agrees with the one for matrices given in the introduction to this article, if we take as H the Hilbert space Cn with the standard dot product and interpret a square matrix as a linear operator on this Hilbert space. It is however much more general as there are important infinite-dimensional Hilbert spaces.
The spectrum of any bounded symmetric operator is real; in particular all its eigenvalues are real, although a symmetric operator may have no eigenvalues.
A general version of the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
which also applies to bounded symmetric operators (see Read and Simon, vol. 1, chapter VII, or other books cited) is stated below. If the set of eigenvalues for a symmetric operator is non empty, and the eigenvalues are nondegenerate, then it follows from the definition that eigenvectors corresponding to distinct eigenvalues are orthogonal.
Contrary to what is sometimes claimed in introductory physics textbooks, it is possible for symmetric operators to have no eigenvalues at all (although the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of any self-adjoint operator is nonempty). The example below illustrates the special case when an (unbounded) symmetric operator does have a set of eigenvectors which constitute a Hilbert space basis. The operator A below can be seen to have a compact
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
inverse, meaning that the corresponding differential equation A f = g is solved by some integral, therefore compact, operator G. The compact symmetric operator G then has a countable family of eigenvectors which are complete in
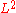 . The same can then be said for A.
. The same can then be said for A.Example. Consider the complex Hilbert space L2[0,1] and the differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
defined on the subspace consisting of all complex-valued infinitely differentiable functions f on [0,1] with the boundary conditions:
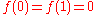
Then integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
shows that A is symmetric. Its eigenfunctions are the sinusoids

with the real eigenvalues n2π2; the well-known orthogonality of the sine functions follows as a consequence of the property of being symmetric.
We consider generalizations of this operator below.
Self-adjoint operators
Given a densely defined linear operator A on H, its adjoint A* is defined as follows:- The domain of A* consists of vectors x in H such that
- (which is a densely defined linear map) is a continuous linear functional. By continuity and density of the domain of A, it extends to a unique continuous linear functional on all of H.
- By the Riesz representation theoremRiesz representation theoremThere are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
for linear functionals, if x is in the domain of A*, there is a unique vector z in H such that
-
- This vector z is defined to be A* x. It can be shown that the dependence of z on x is linear.
Notice that it is the denseness of the domain of the operator, along with the uniqueness part of Riesz representation, that ensures the adjoint operator is well defined.
A result of Hellinger-Toeplitz type says that an operator having an everywhere defined bounded adjoint is bounded.
The condition for a linear operator on a Hilbert space to be self-adjoint is stronger than to be symmetric.
For any densely defined operator A on Hilbert space one can define its adjoint operator A*.
For a symmetric operator A, the domain of the operator A* contains the domain of the operator A, and the restriction of the operator A* on the domain of A coincides with the operator A, i.e.
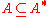 , in other words A* is extension of A. For a self-adjoint operator A the domain of A* is the same as the domain of A, and A=A*. See also Extensions of symmetric operators
, in other words A* is extension of A. For a self-adjoint operator A the domain of A* is the same as the domain of A, and A=A*. See also Extensions of symmetric operatorsExtensions of symmetric operators
In functional analysis, one is interested in extensions of symmetric operators acting on a Hilbert space. Of particular importance is the existence, and sometimes explicit constructions, of self-adjoint extensions. This problem arises, for example, when one needs to specify domains of...
and unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
.
Geometric interpretation
There is a useful geometrical way of looking at the adjoint of an operator A on H as follows: we consider the graph G(A) of A defined by
Theorem. Let J be the symplectic mapping
given by
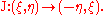
Then the graph of A* is the orthogonal complement of JG(A):
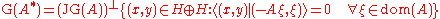
A densely defined operator A is symmetric if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
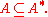
where the subset notation
 is understood to mean
is understood to mean 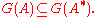 An operator A is self-adjoint if and only if
An operator A is self-adjoint if and only if 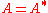 ; that is, if and only if
; that is, if and only if 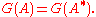
Example. Consider the complex Hilbert space L2(R), and the operator which multiplies a given function by x:
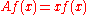
The domain of A is the space of all L2 functions for which the right-hand-side is square-integrable. A is a symmetric operator without any eigenvalues and eigenfunctions. In fact it turns out that the operator is self-adjoint, as follows from the theory outlined below.
As we will see later, self-adjoint operators have very important spectral properties; they are in fact multiplication operators on general measure spaces.
Spectral theorem
Partially defined operators A, B on Hilbert spaces H, K are unitarily equivalent if and only if there is a unitary transformationUnitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
U:H → K such that
- U maps dom A bijectively onto dom B,
A multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
is defined as follows: Let
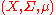 be a countably additive measure space and f a real-valued measurable function on X. An operator T of the form
be a countably additive measure space and f a real-valued measurable function on X. An operator T of the form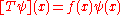
whose domain is the space of ψ for which the right-hand side above is in L2 is called a multiplication operator.
Theorem. Any multiplication operator is a (densely defined) self-adjoint operator. Any self-adjoint operator is unitarily equivalent to a multiplication operator.
This version of the spectral theorem for self-adjoint operators can be proved by reduction to the spectral theorem for unitary operators. This reduction uses the Cayley transform for self-adjoint operators which is defined in the next section. We might note that if T is multiplication by f, then the spectrum of T is just the essential range
Essential range
In mathematics, particularly measure theory, the essential range of a function is intuitively the 'non-negligible' range of the function. One way of thinking of the essential range of a function is the set on which the range of the function is most 'concentrated'...
of f.
Borel functional calculus
Given the representation of T as a multiplication operator, it is easy to characterize the Borel functional calculusBorel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
: If h is a bounded real-valued Borel function on R, then h(T) is the operator of multiplication by the composition
 . In order for this to be well-defined, we must show that it is the unique operation on bounded real-valued Borel functions satisfying a number of conditions.
. In order for this to be well-defined, we must show that it is the unique operation on bounded real-valued Borel functions satisfying a number of conditions.Resolution of the identity
It has been customary to introduce the following notation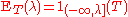
where
 denotes the function which is identically 1 on the interval
denotes the function which is identically 1 on the interval  . The family of projection operators ET(λ) is called resolution of the identity for T. Moreover, the following Stieltjes integral representation for T can be proved:
. The family of projection operators ET(λ) is called resolution of the identity for T. Moreover, the following Stieltjes integral representation for T can be proved: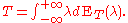
The definition of the operator integral above can be reduced to that that of a scalar valued Stieltjes integral using the weak operator topology. In more modern treatments however, this representation is usually avoided, since most technical problems can be dealt with by the functional calculus.
Formulation in the physics literature
In physics, particularly in quantum mechanics, the spectral theorem is expressed in a way which combines the spectral theorem as stated above and the Borel functional calculusBorel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
using Dirac notation as follows:
If H is Hermitian (the name for self-adjoint in the physics literature) and f is a Borel function,

with
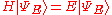
where the integral runs over the whole spectrum of H. The notation suggests that H is diagonalized by the eigenvalues ΨE. Such a notation is purely formal
Formal calculation
In mathematical logic, a formal calculation is sometimes defined as a calculation which is systematic, but without a rigorous justification. This means that we are manipulating the symbols in an expression using a generic substitution, without proving that the necessary conditions hold...
. One can see the similarity between Dirac's notation and the previous section. The resolution of the identity (sometimes called projection valued measures) formally resembles the rank-1 projections
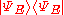 .
.In the Dirac notation, (projective) measurements are described via eigenvalues and eigenstates, both purely formal objects. As one would expect, this does not survive passage to the resolution of the identity. In the latter formulation, measurements are described using the spectral measure of
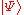 , if the system is prepared in
, if the system is prepared in 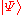 prior to the measurement. Alternatively, if one would like to preserve the notion of eigenstates and make it rigorous, rather than merely formal, one can replace the state space by a suitable rigged Hilbert space
prior to the measurement. Alternatively, if one would like to preserve the notion of eigenstates and make it rigorous, rather than merely formal, one can replace the state space by a suitable rigged Hilbert spaceRigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
.
If f=1, the theorem is referred to as resolution of unity:

In the case
 is the sum of an Hermitian H and a skew-Hermitian (see skew-Hermitian matrix
is the sum of an Hermitian H and a skew-Hermitian (see skew-Hermitian matrixSkew-Hermitian matrix
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
) operator
 , one defines the biorthogonal basis set
, one defines the biorthogonal basis set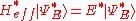
and write the spectral theorem as:

(See Feshbach–Fano partitioning method for the context where such operators appear in scattering theory
Scattering theory
In mathematics and physics, scattering theory is a framework for studying and understanding the scattering of waves and particles. Prosaically, wave scattering corresponds to the collision and scattering of a wave with some material object, for instance sunlight scattered by rain drops to form a...
).
Extensions of symmetric operators
The following question arises in several contexts: if an operator A on the Hilbert space H is symmetric, when does it have self-adjoint extensions? One answer is provided by the Cayley transformCayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
of a self-adjoint operator and the deficiency indices. (We should note here that it is often of technical convenience to deal with closed operator
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
s. In the symmetric case, the closedness requirement poses no obstacles, since it is known that all symmetric operators are closable.)
Theorem. Suppose A is a symmetric operator. Then there is a
unique partially defined linear operator
such that
Here, ran and dom denote the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
and the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, respectively. W(A) is isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
on its domain. Moreover, the range of 1 − W(A) is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in H.
Conversely, given any partially defined operator U which is isometric on its domain (which is not
necessarily closed) and such that 1 − U is dense, there is a (unique) operator S(U)
such that
The operator S(U) is densely defined and symmetric.
The mappings W and S are inverses of each other.
The mapping W is called the Cayley transform. It associates a partially defined isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
to any symmetric densely-defined operator. Note that the mappings W and S are : This means that if B is a symmetric operator that extends the densely defined symmetric operator A, then W(B) extends W(A), and similarly for S.
Theorem. A necessary and sufficient condition for A to be self-adjoint is that its Cayley transform W(A) be unitary.
This immediately gives us a necessary and sufficient condition for A to have a self-adjoint extension, as follows:
Theorem. A necessary and sufficient condition for A to have a self-adjoint extension is that W(A) have a unitary extension.
A partially defined isometric operator V on a Hilbert space H has a unique isometric extension to the norm closure of dom(V). A partially defined isometric operator with closed domain is called a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
.
Given a partial isometry V, the deficiency indices of V are defined as the dimension of the orthogonal complements of the domain and range:


Theorem. A partial isometry V has a unitary extension if and only if the deficiency indices are identical. Moreover, V has a unique unitary extension if and only if the both deficiency indices are zero.
We see that there is a bijection between symmetric extensions of an operator and isometric extensions of its Cayley transform. An operator which has a unique self-adjoint extension is said to be essentially self-adjoint. Such operators have a well-defined Borel functional calculus
Borel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
. Symmetric operators which are not essentially self-adjoint may still have a canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
self-adjoint extension. Such is the case for non-negative symmetric operators (or more generally, operators which are bounded below). These operators always have a canonically defined Friedrichs extension
Friedrichs extension
In functional analysis, the Friedrichs extension is a canonical self-adjoint extension of a non-negative densely defined symmetric operator. It is named after the mathematician Kurt Friedrichs...
and for these operators we can define a canonical functional calculus. Many operators that occur in analysis are bounded below (such as the negative of the Laplacian operator), so the issue of essential adjointness for these operators is less critical.
Self-adjoint extensions in quantum mechanics
In quantum mechanics, observables correspond to self-adjoint operators. By Stone's theorem, self-adjoint operators are precisely the infinitesimal generators of unitary groups of time evolutionTime evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
operators. However, many physical problems are formulated as a time-evolution equation involving differential operators for which the Hamiltonian is only symmetric. In such cases, either the Hamiltonian is essentially self-adjoint, in which case the physical problem has unique solutions or one attempts to find self-adjoint extensions of the Hamiltonian corresponding to different types of boundary conditions or conditions at infinity.
Example. The one-dimensional Schrödinger operator with the potential
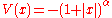 , defined initially on smooth compactly supported functions, is essentially self-adjoint (that is, has a self-adjoint closure) for
, defined initially on smooth compactly supported functions, is essentially self-adjoint (that is, has a self-adjoint closure) for  but not for
but not for  See Berezin and Schubin, page 55.
See Berezin and Schubin, page 55.Example. There is no self-adjoint momentum operator
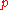 for a particle moving on a half-line. Nevertheless, the Hamiltonian
for a particle moving on a half-line. Nevertheless, the Hamiltonian 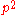 of a "free" particle on a half-line has several self-adjoint extensions corresponding to different types of boundary conditions. Physically, these boundary conditions are related to reflections of the particle at the origin (see Reed and Simon, vol.2).
of a "free" particle on a half-line has several self-adjoint extensions corresponding to different types of boundary conditions. Physically, these boundary conditions are related to reflections of the particle at the origin (see Reed and Simon, vol.2).Von Neumann's formulas
Suppose A is symmetric; any symmetric extension of A is a restriction of A*; Indeed if B is symmetric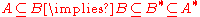
Theorem. Suppose A is a densely defined symmetric operator. Let

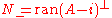
Then


and

where the decomposition is orthogonal relative to the graph inner product of dom(A*):
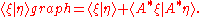
These are referred to as von Neumann's formulas in the Akhiezer and Glazman reference.
Examples
We first consider the differential operatordefined on the space of complex-valued C∞ functions on [0,1] vanishing near 0 and 1. D is a symmetric operator as can be shown by integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
. The spaces N+, N− are given respectively by the distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
al solutions to the equation


which are in L2 [0,1]. One can show that each one of these solution spaces is 1-dimensional, generated by the functions
x → eix and x → e−ix respectively. This shows that D is not essentially self-adjoint, but does have self-adjoint extensions. These self-adjoint extensions are parametrized by the space of unitary mappings
which in this case happens to be the unit circle T.
This simple example illustrates a general fact about self-adjoint extensions of symmetric differential operators P on an open set M. They are determined by the unitary maps between the eigenvalue spaces
where Pdist is the distributional extension of P.
We next give the example of differential operators with constant coefficients. Let
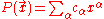
be a polynomial on Rn with real coefficients, where α ranges over a (finite) set of multi-indices. Thus
and
We also use the notation
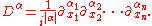
Then the operator P(D) defined on the space of infinitely differentiable functions of compact support on Rn by

is essentially self-adjoint on L2(Rn).
Theorem. Let P a polynomial function on Rn with real coefficients, F the Fourier transform considered as a unitary map L2(Rn) → L2(Rn). Then F* P(D) F is essentially self-adjoint and its unique self-adjoint extension is the operator of multiplication by the function P.
More generally, consider linear differential operators acting on infinitely differentiable complex-valued functions of compact support. If M is an open subset of Rn
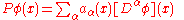
where aα are (not necessarily constant) infinitely differentiable functions. P is a linear operator
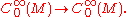
Corresponding to P there is another differential operator, the formal adjoint of P

Theorem. The operator theoretic adjoint P* of P is a restriction of the distributional extension of the formal adjoint. Specifically:
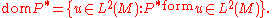
Spectral multiplicity theory
The multiplication representation of a self-adjoint operator, though extremely useful, is not a canonical representation. This suggests that it is not easy to extract from this representation a criterion to determine when self-adjoint operators A and B are unitarily equivalent. The finest grained representation which we now discuss involves spectral multiplicity. This circle of results is called the HahnHans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
-Hellinger
Ernst Hellinger
Ernst David Hellinger was a German mathematician.-Early years:Ernst Hellinger was born on September 30, 1883 in Striegau, Silesia, Germany to Emil and Julie Hellinger. He grew up in Breslau, attended school and graduated from the Gymnasium there in 1902...
theory of spectral multiplicity.
We first define uniform multiplicity:
Definition. A self-adjoint operator A has uniform multiplicity n where n is such that 1 ≤ n ≤ ω
if and only if A is unitarily equivalent to the operator Mf of multiplication by the function f(λ) = λ on

where Hn is a Hilbert space of dimension n. The domain of Mf consists of vector-valued functions ψ on R such that
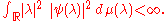
Non-negative countably additive measures μ, ν are mutually singular if and only if they are supported on disjoint Borel sets.
Theorem. Let A be a self-adjoint operator on a separable Hilbert space H. Then there is an ω sequence of countably additive finite measures on R (some of which may be identically 0)
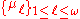
such that the measures are pairwise singular and A is unitarily equivalent to the operator of multiplication by the function f(λ) = λ on
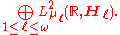
This representation is unique in the following sense: For any two such representations of the same A, the corresponding measures are equivalent in the sense that they have the same sets of measure 0.
The spectral multiplicity theorem can be reformulated using the language of direct integral
Direct integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
s of Hilbert spaces:
Theorem. Any self-adjoint operator on a separable Hilbert space is unitarily equivalent to multiplication by the function λ → λ on
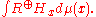
The measure equivalence class of μ (or equivalently its sets of measure 0) is uniquely determined and the measurable family
{Hx}x is determined almost everywhere with respect to μ.
Example: structure of the Laplacian
The Laplacian on Rn is the operator
As remarked above, the Laplacian is diagonalized by the Fourier transform. Actually it is more natural to consider the negative of the Laplacian - Δ since as an operator it is non-negative; (see elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
).
Theorem. If n=1, then -Δ has uniform multiplicity mult=2, otherwise -Δ has uniform multiplicity mult=ω. Moreover, the measure μmult is Borel measure on
Pure point spectrum
A self-adjoint operator A on H has pure point spectrum if and only if H has an orthonormal basis {ei}i ∈ I consisting of eigenvectors for A.Example. The Hamiltonian for the harmonic oscillator has a quadratic potential V, that is

This Hamiltonian has pure point spectrum; this is typical for bound state Hamiltonians
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
in quantum mechanics. As was pointed out in a previous example, a sufficient condition that an unbounded symmetric operator has eigenvectors which form a Hilbert space basis is that it has a compact inverse.
See also
- Compact operator on Hilbert spaceCompact operator on Hilbert spaceIn functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
- Theoretical and experimental justification for the Schrödinger equationTheoretical and experimental justification for the Schrödinger equationThe theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles...
- Unbounded operatorUnbounded operatorIn mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....