
Maximum principle
Encyclopedia
In mathematics
, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic
types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain. Specifically, the strong maximum principle says that if a function achieves its maximum in the interior of the domain, the function is uniformly a constant. The weak maximum principle says that the maximum of the function is to be found on the boundary, but may re-occur in the interior as well. Other, even weaker maximum principles exist which merely bound a function in terms of its maximum on the boundary.
In convex optimization, the maximum principle states that the maximum of a convex function
on a compact convex set
is attained on the boundary
.
, then f cannot exhibit a true local maximum within the domain of definition of f. In other words, either f is a constant function
, or, for any point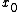 inside the domain of f, there exist other points arbitrarily close to
inside the domain of f, there exist other points arbitrarily close to 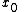 at which f takes larger values.
at which f takes larger values.
Let f be defined on some connected
open
subset
D of the Euclidean space
Rn. If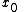 is a point in D such that
is a point in D such that

for all x in a neighborhood of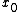 , then the function f is constant on D.
, then the function f is constant on D.
By replacing "maximum" with "minimum" and "larger" with "smaller", one obtains the minimum principle for harmonic functions.
The maximum principle also holds for the more general subharmonic function
s, while superharmonic functions satisfy the minimum principle.
 is a non-degenerate critical point
is a non-degenerate critical point
of f(x), we must be seeing a saddle point
, since otherwise there is no chance that the sum of the second derivatives of f is zero. This of course is not a complete proof, and we left out the case of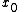 being a degenerate point, but this is the essential idea.
being a degenerate point, but this is the essential idea.
The strong maximum principle relies on the Hopf lemma, and this is more complicated.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain. Specifically, the strong maximum principle says that if a function achieves its maximum in the interior of the domain, the function is uniformly a constant. The weak maximum principle says that the maximum of the function is to be found on the boundary, but may re-occur in the interior as well. Other, even weaker maximum principles exist which merely bound a function in terms of its maximum on the boundary.
In convex optimization, the maximum principle states that the maximum of a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
on a compact convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is attained on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
.
The classical example
Harmonic functions are the classical example to which the strong maximum principle applies. Formally, if f is a harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
, then f cannot exhibit a true local maximum within the domain of definition of f. In other words, either f is a constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
, or, for any point
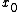 inside the domain of f, there exist other points arbitrarily close to
inside the domain of f, there exist other points arbitrarily close to 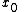 at which f takes larger values.
at which f takes larger values.Let f be defined on some connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
D of the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. If
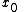 is a point in D such that
is a point in D such that
for all x in a neighborhood of
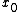 , then the function f is constant on D.
, then the function f is constant on D.By replacing "maximum" with "minimum" and "larger" with "smaller", one obtains the minimum principle for harmonic functions.
The maximum principle also holds for the more general subharmonic function
Subharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
s, while superharmonic functions satisfy the minimum principle.
Heuristics for the proof
The weak maximum principle for harmonic functions is a simple consequence of facts from calculus. The key ingredient for the proof is the fact that, by the definition of a harmonic function, the Laplacian of f is zero. Then, if is a non-degenerate critical point
is a non-degenerate critical pointCritical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of f(x), we must be seeing a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
, since otherwise there is no chance that the sum of the second derivatives of f is zero. This of course is not a complete proof, and we left out the case of
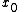 being a degenerate point, but this is the essential idea.
being a degenerate point, but this is the essential idea.The strong maximum principle relies on the Hopf lemma, and this is more complicated.

