Ornstein-Uhlenbeck process
Encyclopedia
In mathematics, the Ornstein–Uhlenbeck process (named after Leonard Ornstein
and George Eugene Uhlenbeck
), is a stochastic process
that, roughly speaking, describes the velocity of a massive Brownian particle
under the influence of friction. The process is stationary
, Gaussian
, and Markov
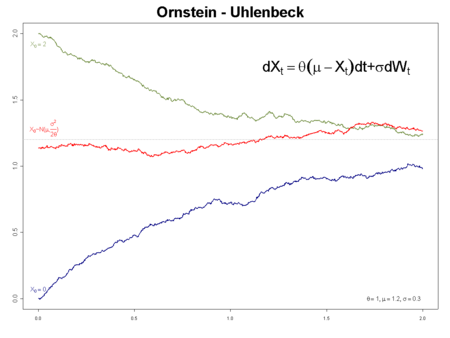
, and is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables. Over time, the process tends to drift towards its long-term mean: such a process is called mean-reverting.
The process can be considered to be a modification of the random walk
in continuous time, or Wiener process
, in which the properties of the process have been changed so that there is a tendency of the walk to move back towards a central location, with a greater attraction when the process is further away from the centre. The Ornstein–Uhlenbeck process can also be considered as the continuous-time analogue of the discrete-time
AR(1) process.
:
where
, 
and 
are parameters and 
denotes the Wiener process
.
The above representation can be taken as the primary definition of an Ornstein–Uhlenbeck process, although the process is equally well-defined by the requirements that a stochastic process
be stationary
, Gaussian
, and a Markov process
.
Consider for example a Hookean spring
with spring constant
whose dynamics is highly overdamped
with friction coefficient
.
In the presence of thermal fluctuations with temperature
, the length 
of the spring will fluctuate stochastically around the spring rest length
;
its stochastic dynamic is described by an Ornstein–Uhlenbeck process with:
Leonard Ornstein
Leonard Salomon Ornstein was a Dutch physicist. He studied theoretical physics with Hendrik Antoon Lorentz at University of Leiden. He subsequently carried out Ph.D. research under the supervision of Lorentz, concerning an application of the statistical mechanics of Gibbs to molecular problems...
and George Eugene Uhlenbeck
George Eugene Uhlenbeck
George Eugene Uhlenbeck was a Dutch-American theoretical physicist.-Background and education:George Uhlenbeck was the son of Eugenius and Anne Beeger Uhlenbeck...
), is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
that, roughly speaking, describes the velocity of a massive Brownian particle
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
under the influence of friction. The process is stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, Gaussian
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
, and Markov
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
, and is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables. Over time, the process tends to drift towards its long-term mean: such a process is called mean-reverting.
The process can be considered to be a modification of the random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
in continuous time, or Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
, in which the properties of the process have been changed so that there is a tendency of the walk to move back towards a central location, with a greater attraction when the process is further away from the centre. The Ornstein–Uhlenbeck process can also be considered as the continuous-time analogue of the discrete-time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
AR(1) process.
Representation via a stochastic differential equation
An Ornstein–Uhlenbeck process, xt, satisfies the following stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
:
where
, and are parameters and denotes the Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
.
The above representation can be taken as the primary definition of an Ornstein–Uhlenbeck process, although the process is equally well-defined by the requirements that a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
be stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, Gaussian
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
, and a Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
.
Application in physical sciences
The Ornstein–Uhlenbeck process is a prototype of a noisy relaxation process.Consider for example a Hookean spring
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
with spring constant
whose dynamics is highly overdampedwith friction coefficient
.In the presence of thermal fluctuations with temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, the length of the spring will fluctuate stochastically around the spring rest length
;its stochastic dynamic is described by an Ornstein–Uhlenbeck process with:
-
where
is derived from the Stokes–Einstein equation 
for the effective diffusion constant.
In physical sciences, the stochastic differential equation of an Ornstein–Uhlenbeck process is rewritten as a Langevin equationLangevin equationIn statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
where
is white Gaussian noiseGaussian noiseGaussian noise is statistical noise that has its probability density function equal to that of the normal distribution, which is also known as the Gaussian distribution. In other words, the values that the noise can take on are Gaussian-distributed. A special case is white Gaussian noise, in which...
with
At equilibrium, the spring stores an average energy
in accordance with the equipartition theoremEquipartition theoremIn classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
.
Application in financial mathematics
The Ornstein–Uhlenbeck process is one of several approaches used to model (with modifications) interest rates, currency exchange rates, and commodity prices stochastically. The parameter
represents the equilibrium or mean value supported by fundamentals; 
the degree of volatility around it caused by shocks, and 
the rate by which these shocks dissipate and the variable reverts towards the mean. One application of the process is a trading strategy known as pairs tradePairs tradeThe pairs trade or pair trading is a market neutral trading strategy enabling traders to profit from virtually any market conditions: uptrend, downtrend, or sideways movement. This strategy is categorized as a statistical arbitrage and convergence trading strategy...
.
Mathematical properties
The Ornstein–Uhlenbeck process is an example of a Gaussian processGaussian processIn probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
that has a bounded variance and admits a stationaryStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, in contrast to the Wiener processWiener processIn mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
; the difference between the two is in their "drift" term. For the Wiener process the drift term is constant, whereas for the Ornstein–Uhlenbeck process it is dependent on the current value of the process: if the current value of the process is less than the (long-term) mean, the drift will be positive; if the current value of the process is greater than the (long-term) mean, the drift will be negative. In other words, the mean acts as an equilibrium level for the process. This gives the process its informative name, "mean-reverting." The stationary (long-term) varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is given by
The Ornstein–Uhlenbeck process is the continuous-time analogue of the discrete-timeDiscrete timeDiscrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
AR(1) process.
Solution
This equation is solved by variation of parameters. Apply Itō–Doeblin's formula to the function
to get
Integrating from 0 to t we get
whereupon we see
Formulae for moments
From this representation, the first momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
is given by (assuming that x0 is a constant)
The Itō isometryIto isometryIn mathematics, the Itō isometry, named after Kiyoshi Itō, is a crucial fact about Itō stochastic integrals. One of its main applications is to enable the computation of variances for stochastic processes....
can be used to calculate the covariance functionCovariance functionIn probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
by
-
Thus if s < t (so that min(s, t) = s), then we have
Alternative representation
It is also possible (and often convenient) to represent xt (unconditionally, i.e. as
) as a scaled time-transformed Wiener process:
or conditionally (given x0) as
The time integral of this process can be used to generate noise with a 1/ƒ power spectrumPink noisePink noise or 1/ƒ noise is a signal or process with a frequency spectrum such that the power spectral density is inversely proportional to the frequency. In pink noise, each octave carries an equal amount of noise power...
.
Scaling limit interpretation
The Ornstein–Uhlenbeck process can be interpreted as a scaling limitScaling limitIn physics or mathematics, the scaling limit is a term applied to the behaviour of a lattice model in the limit of the lattice spacing going to zero. A lattice model which approximates a continuum quantum field theory in the limit as the lattice spacing goes to zero corresponds to finding a second...
of a discrete process, in the same way that Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
is a scaling limit of random walks. Consider an urn containing
blue and yellow balls. At each step a ball is chosen at random and replaced by a ball of the opposite colour. Let 
be the number of blue balls in the urn after 
steps. Then 
converges to a Ornstein–Uhlenbeck process as 
tends to infinity.
Fokker–Planck equation representation
The probability density function ƒ(x, t) of the Ornstein–Uhlenbeck process satisfies the Fokker–Planck equation
The general solution of this equation, taking
and 
for simplicity, and the initial condition 
is,
The stationary solution of this equation is the limit for time tending to infinity which is a Gaussian distribution with mean
and variance
Generalizations
It is possible to extend Ornstein–Uhlenbeck processes to processes where the background driving process is a Lévy processLévy processIn probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
. These processes are widely studied by Ole Barndorff-Nielsen and Neil ShephardNeil ShephardNeil Shephard , FBA, is a British economist, currently Professor of Economics at the University of Oxford. He is also a Professorial Fellow of Nuffield College, Oxford and member of the Oxford-Man Institute....
, and others.
In addition, in finance, stochastic processes are used the volatility increases for larger
values of
. In particular, the CKLS (Chan–Karolyi–Longstaff–Sanders) process with the volatility term replaced by 
can be solved in closed form for 
or 1, as well as for 
, which corresponds to the conventional OU process.
See also
- The Vasicek modelVasicek modelIn finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of "one-factor model" as it describes interest rate movements as driven by only one source of market risk...
of interest rates is an example of an Ornstein–Uhlenbeck process. - Short rate modelShort rate modelIn the context of interest rate derivatives, a short-rate model is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,.-The short rate:...
– contains more examples.
External links
- A Stochastic Processes Toolkit for Risk Management, Damiano Brigo, Antonio Dalessandro, Matthias Neugebauer and Fares Triki
- Simulating and Calibrating the Ornstein–Uhlenbeck process, M.A. van den Berg
- Calibrating the Ornstein-Uhlenbeck model, M.A. van den Berg
- Maximum likelihood estimation of mean reverting processes, Jose Carlos Garcia Franco
-
-
