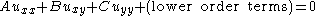Hyperbolic partial differential equation
Encyclopedia
In mathematics
, a hyperbolic partial differential equation of order n is a partial differential equation
(PDE) that, roughly speaking, has a well-posed initial value problem
for the first n−1 derivatives. More precisely, the Cauchy problem
can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics
are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation
. In one spatial dimension, this is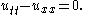
The equation has the property that, if u and its first time derivative are arbitrarily specified initial data on the initial line t = 0 (with sufficient smoothness properties), then there exists a solution for all time.
The solutions of hyperbolic equations are "wave-like." If a disturbance is made in the initial data of a hyperbolic differential equation, then not every point of space feels the disturbance at once. Relative to a fixed time coordinate, disturbances have a finite propagation speed. They travel along the characteristics
of the equation. This feature qualitatively distinguishes hyperbolic equations from elliptic partial differential equations and parabolic partial differential equation
s. A perturbation of the initial (or boundary) data of an elliptic or parabolic equation is felt at once by essentially all points in the domain.
Although the definition of hyperbolicity is fundamentally a qualitative one, there are precise criteria that depend on the particular kind of differential equation under consideration. There is a well-developed theory for linear differential operators, due to Lars Gårding
, in the context of microlocal analysis
. Nonlinear differential equations are hyperbolic if their linearizations are hyperbolic in the sense of Gårding. There is a somewhat different theory for first order systems of equations coming from systems of conservation law
s.
is uniquely solvable in a neighborhood of P for any initial data given on a non-characteristic hypersurface passing through P. Here the prescribed initial data consists of all (transverse) derivatives of the function on the surface up to one less than the order of the differential equation.
with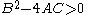
can be transformed to the wave equation, apart from lower order terms which are inessential for the qualitative understanding of the equation. This definition is analogous to the definition of a planar hyperbola.
The one-dimensional wave equation
:

is an example of a hyperbolic equation. The two-dimensional and three-dimensional wave equations also fall into the category of hyperbolic PDE.
This type of second-order hyperbolic partial differential equation may be transformed to a hyperbolic system of first-order differential equations.
 first order partial differential equations for
first order partial differential equations for  unknown function
unknown function
s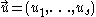 ,
, 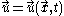 , where
, where 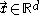
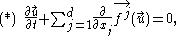
 are once continuously
are once continuously
differentiable
functions, nonlinear in general.
Now define for each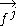 a matrix
a matrix
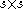
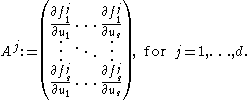
We say that the system is hyperbolic if for all
is hyperbolic if for all 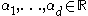 the matrix
the matrix 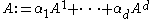
has only real
eigenvalues and is diagonalizable
.
If the matrix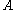 has distinct real eigenvalues, it follows that it's diagonalizable. In this case the system
has distinct real eigenvalues, it follows that it's diagonalizable. In this case the system 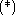 is called strictly hyperbolic.
is called strictly hyperbolic.
. Consider a hyperbolic system of one partial differential equation for one unknown function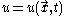 . Then the system
. Then the system 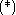 has the form
has the form
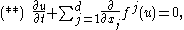
Now can be some quantity with a flux
can be some quantity with a flux
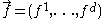 . To show that this quantity is conserved, integrate
. To show that this quantity is conserved, integrate
 over a domain
over a domain 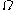
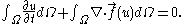
If and
and 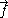 are sufficiently smooth functions, we can use the divergence theorem
are sufficiently smooth functions, we can use the divergence theorem
and change the order of the integration and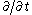 to get a conservation law for the quantity
to get a conservation law for the quantity  in the general form
in the general form
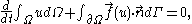
which means that the time rate of change of in the domain
in the domain 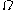 is equal to the net flux of
is equal to the net flux of  through its boundary
through its boundary 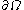 . Since this is an equality, it can be concluded that
. Since this is an equality, it can be concluded that  is conserved within
is conserved within 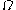 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a hyperbolic partial differential equation of order n is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE) that, roughly speaking, has a well-posed initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
for the first n−1 derivatives. More precisely, the Cauchy problem
Cauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. In one spatial dimension, this is
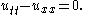
The equation has the property that, if u and its first time derivative are arbitrarily specified initial data on the initial line t = 0 (with sufficient smoothness properties), then there exists a solution for all time.
The solutions of hyperbolic equations are "wave-like." If a disturbance is made in the initial data of a hyperbolic differential equation, then not every point of space feels the disturbance at once. Relative to a fixed time coordinate, disturbances have a finite propagation speed. They travel along the characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
of the equation. This feature qualitatively distinguishes hyperbolic equations from elliptic partial differential equations and parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s. A perturbation of the initial (or boundary) data of an elliptic or parabolic equation is felt at once by essentially all points in the domain.
Although the definition of hyperbolicity is fundamentally a qualitative one, there are precise criteria that depend on the particular kind of differential equation under consideration. There is a well-developed theory for linear differential operators, due to Lars Gårding
Lars Gårding
Lars Gårding is a Swedish mathematician. He has made notable contributions to the study of partial differential operators. He is a professor emeritus of mathematics at Lund University in Sweden...
, in the context of microlocal analysis
Microlocal analysis
In mathematical analysis, microlocal analysis comprises techniques developed from the 1950s onwards based on Fourier transforms related to the study of variable-coefficients-linear and nonlinear partial differential equations...
. Nonlinear differential equations are hyperbolic if their linearizations are hyperbolic in the sense of Gårding. There is a somewhat different theory for first order systems of equations coming from systems of conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
s.
Definition
A partial differential equation is hyperbolic at a point P provided that the Cauchy problemCauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
is uniquely solvable in a neighborhood of P for any initial data given on a non-characteristic hypersurface passing through P. Here the prescribed initial data consists of all (transverse) derivatives of the function on the surface up to one less than the order of the differential equation.
Examples
By a linear change of variables, any equation of the formwith
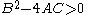
can be transformed to the wave equation, apart from lower order terms which are inessential for the qualitative understanding of the equation. This definition is analogous to the definition of a planar hyperbola.
The one-dimensional wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
:

is an example of a hyperbolic equation. The two-dimensional and three-dimensional wave equations also fall into the category of hyperbolic PDE.
This type of second-order hyperbolic partial differential equation may be transformed to a hyperbolic system of first-order differential equations.
Hyperbolic system of partial differential equations
Consider the following system of first order partial differential equations for
first order partial differential equations for  unknown function
unknown functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s
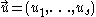 ,
, 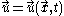 , where
, where 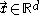
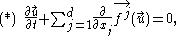
 are once continuously
are once continuouslyContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
functions, nonlinear in general.
Now define for each
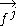 a matrix
a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
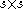
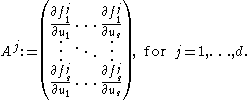
We say that the system
 is hyperbolic if for all
is hyperbolic if for all 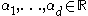 the matrix
the matrix 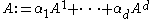
has only real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
eigenvalues and is diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
.
If the matrix
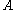 has distinct real eigenvalues, it follows that it's diagonalizable. In this case the system
has distinct real eigenvalues, it follows that it's diagonalizable. In this case the system 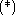 is called strictly hyperbolic.
is called strictly hyperbolic.Hyperbolic system and conservation laws
There is a connection between a hyperbolic system and a conservation lawConservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
. Consider a hyperbolic system of one partial differential equation for one unknown function
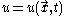 . Then the system
. Then the system 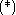 has the form
has the form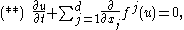
Now
 can be some quantity with a flux
can be some quantity with a fluxFlux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
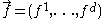 . To show that this quantity is conserved, integrate
. To show that this quantity is conserved, integrateIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
 over a domain
over a domain 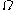
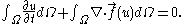
If
 and
and 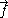 are sufficiently smooth functions, we can use the divergence theorem
are sufficiently smooth functions, we can use the divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
and change the order of the integration and
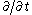 to get a conservation law for the quantity
to get a conservation law for the quantity  in the general form
in the general form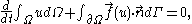
which means that the time rate of change of
 in the domain
in the domain 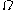 is equal to the net flux of
is equal to the net flux of  through its boundary
through its boundary 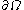 . Since this is an equality, it can be concluded that
. Since this is an equality, it can be concluded that  is conserved within
is conserved within 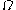 .
.See also
- Elliptic partial differential equationElliptic operatorIn the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
- Parabolic partial differential equationParabolic partial differential equationA parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
- Hypoelliptic operator
- Relativistic heat conductionRelativistic heat conductionThe theory of relativistic heat conduction claims to be the only model for heat conduction that is compatible with the theory of special relativity, the second law of thermodynamics, electrodynamics, and quantum mechanics, simultaneously...
External links
- Linear Hyperbolic Equations at EqWorld: The World of Mathematical Equations.
- Nonlinear Hyperbolic Equations at EqWorld: The World of Mathematical Equations.