Atiyah–Singer index theorem
Encyclopedia
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator
on a compact manifold, the analytical index (related to the dimension of the space of solutions) is equal to the topological index (defined in terms of some topological data). It includes many other theorems, such as the Riemann–Roch theorem
, as special cases, and has applications in theoretical physics
.
and its generalization the Hirzebruch–Riemann–Roch theorem, and the Hirzebruch signature theorem. Hirzebruch
and Borel
had proved the integrality of the  genus of a spin manifold, and Atiyah suggested that this integrality could be explained if it were the index of the Dirac operator
(which was rediscovered by Atiyah and Singer in 1961).
The Atiyah–Singer theorem was announced by . The proof sketched in this announcement was never published by them, though it appears in the book . Their first published proof replaced the cobordism
theory of the first proof with K-theory
, and they used this to give proofs of various generalizations in the papers .
In 1965, S.P. Novikov published his results on the topological invariance of the rational Pontrjagin classes on smooth manifolds.
Kirby and Siebenmann's results , combined with René Thom's paper proved the existence of rational Pontrjagin classes on topological manifolds. The rational Pontrjagin classes are essential ingredients of the index theorem on smooth and topological manifolds.
In 1969, M.F. Atiyah defines abstract elliptic operators on arbitrary metric spaces. Abstract elliptic operators became protagonists in Kasparov's theory and Connes's noncommutative differential geometry.
In 1971, I.M. Singer proposes a comprehensive program for future extensions of index theory.
In 1972, G.G. Kasparov publishes his work on the realization of the K-homology by abstract elliptic operators.
gave a new proof of the index theorem using the heat equation
, described in .
In 1977, D. Sullivan establishes his theorem on the existence and uniqueness of Lipschitz and quasiconformal structures on topological manifolds of dimension different from 4.
motivated by ideas of and Alvarez-Gaume, gave a short proof of the local index theorem for operators that are locally Dirac operator
s; this covers many of the useful cases.
In 1983, N. Teleman proves that the analytical indices of signature operators with values in vector bundles are topological invariants.
In 1984, N. Teleman establishes the index theorem on topological manifolds.
In 1986, A. Connes publishes his fundamental paper on non-commutative geometry.
In 1989, S.K. Donaldson and D. Sullivan study Yang–Mills theory on quasiconformal manifolds of dimension 4. They introduce the signature operator S defined on differential forms of degree two.
In 1990, A. Connes and H. Moscovici prove the local index formula in the context of non-commutative geometry.
In 1994, A. Connes, D. Sullivan and N. Teleman prove the index theorem for signature operators on quasiconformal manifolds.
then its symbol
is the function of 2k variables
given by dropping all terms of order less than n and replacing ∂/∂xi by yi. So the symbol is homogeneous in the variables y, of degree n. The symbol is well defined even though ∂/∂xi does not commute with xi because we only keep the highest order terms and differential operators commute "up to lower-order terms". The operator is called elliptic if the symbol is nonzero whenever at least one y is nonzero.
Example: The Laplace operator in k variables has symbol y12 + ... + yk2, and so is elliptic as this is nonzero whenever any the yis are nonzero. The wave operator has symbol −y12 + ... + yk2, which is not elliptic if k ≥ 2, as the symbol vanishes for some non-zero values of the ys.
The symbol of a differential operator of order n on a smooth manifold X is defined in much the same way using local coordinate charts, and is a function on the cotangent bundle
of X, homogeneous of degree n on each cotangent space. (In general, differential operators transform in a rather complicated way under coordinate transforms (see jet bundle
); however, the highest order terms transform like tensors so we get well defined homogeneous functions on the cotangent spaces that are independent of the choice of local charts.) More generally, the symbol of a differential operator between two vector bundles E and F is a section of the pullback of the bundle
to the cotangent space of X. The differential operator is called elliptic if the element of Hom(Ex, Fx) is invertible for all non-zero cotangent vectors at any point x of X.
A key property of elliptic operators is that they are almost invertible; this is closely related to the fact that their symbols are almost invertible. More precisely, an elliptic operator D on a compact manifold has a (non-unique) parametrix
(or pseudoinverse) D′ such that DD′ − 1 and D′D − 1 are both compact operators. An important consequence is that the kernel of D is finite-dimensional, because all eigenspaces of compact operators, other than the kernel, are finite-dimensional. (The pseudoinverse of an elliptic differential operator is almost never a differential operator. However, it is an elliptic pseudodifferential operator.)
. Any Fredholm operator has an index, defined as the difference between the (finite) dimension of the kernel
of D (solutions of Df = 0), and the (finite) dimension of the cokernel
of D (the constraints on the right-hand-side of an inhomogeneous equation like Df = g, or equivalently the kernel of the adjoint operator). In other words,
This is sometimes called the analytical index of D.
Example. Suppose that the manifold is the circle (thought of as R/Z), and D is the operator d/dx − λ for some complex constant λ. (This is the simplest example of an elliptic operator.) Then the kernel is the space of multiples of exp(λx) if λ is an integral multiple of 2πi and is 0 otherwise, and the kernel of the adjoint is a similar space with λ replaced by its complex conjugate. So D has index 0. This example shows that the kernel and cokernel of elliptic operators can jump discontinuously as the elliptic operator varies, so there is no nice formula for their dimensions in terms of continuous topological data. However the jumps in the dimensions of the kernel and cokernel are the same, so the index, given by the difference of their dimensions, does vary continuously, and can be given in terms of topological data by the index theorem.
in other words the value of the top dimensional component of the mixed cohomology class ch(D)Td(X) on the fundamental homology class of the manifold X.
Here,
of the manifold X.ch( D) is equal to φ−1(ch(d(p*E,p*F, σ(D))), where
φ is the Thom isomorphism from H k(X,Q) to Hn+k(B(X)/S(X),Q)
B(X) is the unit ball bundle of the cotangent bundle of X, and S(X) is its boundary, and p is the projection to X.
ch is the Chern character from K-theory K( X) to the rational cohomology ring H(X,Q).
d( p*E,p*F, σ(D)) is the "difference element" of K(B(X)/S(X)) associated to two vector bundles p*E and p*F on B(X) and an isomorphism σ(D) between them on the subspace S(X).
σ( D) is the symbol of D
Another method of defining the topological index uses K theory. If X is a compact submanifold of a manifold Y then there is a pushforward operation from K(TX) to K(TY). The topological index of an element of
K(TX) is defined to be the image of this operation with Y some Euclidean space, for which K(TY) can be naturally identified with the integers Z. This index is independent of the embedding of X in Euclidean space.
The index problem is the following: compute the (analytical) index of D using only the symbol s and topological data derived from the manifold and the vector bundle. The Atiyah–Singer index theorem solves this problem, and states:
In spite of its formidable definition, the topological index is usually straightforward to evaluate explicitly. So this makes it possible to evaluate the analytical index. (The cokernel and kernel of an elliptic operator are in general extremely hard to evaluate individually; the index theorem shows that we can usually at least evaluate their difference.) Many important invariants of a manifold (such as the signature) can be given as the index of suitable differential operators, so the index theorem allows us to evaluate these invariants in terms of topological data.
Although the analytical index is usually hard to evaluate directly, it is at least obviously an integer. The topological index is by definition a rational number, but it is usually not at all obvious from the definition that it is also integral. So the Atiyah–Singer index theorem implies some deep integrality properties, as it implies that the topological index is integral.
The index of an elliptic differential operator obviously vanishes if the operator is self adjoint. It also vanishes if the manifold X has odd dimension, though there are pseudodifferential elliptic operators whose index does not vanish in odd dimensions.
The proof of this result goes through specific considerations, including the extension of Hodge theory on combinatorial and Lipschitz manifolds , , the extension of Atiyah–Singer's signature operator to Lipschitz manifolds , Kasparov's K-homology and topological cobordism .
This result shows that the index theorem is not merely a differentiable statement, but rather a topological statement.
This theory is based on a signature operator S, defined on middle degree differential forms on even-dimensional quasiconformal manifolds (compare ).
Using topological cobordism and K-homology one may provide a full statement of an index theorem on quasiconformal manifolds (see page 678 of ).
The work "provides local constructions for characteristic classes based on higher dimensional relatives of the measurable Riemann mapping in dimension two and the Yang–Mills theory in dimension four."
These results constitute significant advances along the lines of Singer's program Prospects in Mathematics .
At the same time, they provide, also, an effective construction of the rational Pontrjagin classes on topological manifolds.
The paper provides a link between Thom's original construction of the rational Pontrjagin classes and index theory.
It is important to mention that the index formula is a topological statement. The obstruction theories due to Milnor, Kervaire, Kirby, Siebenmann, Sullivan, Donaldson show that only a minority of topological manifolds possess differentiable structures and these are not necessarily unique. Sullivan's result on Lipschitz and quasiconformal structures shows that any topological manifold in dimension different from 4 possesses such a structure which is unique (up to isotopy close to identity).
The quasiconformal structure is the weakest analytical structure on topological manifolds for which the index theorem is known to hold.
of the Hodge cohomology of M, and the analytical index is the Euler class of the manifold. The index formula for this operator yields the Chern-Gauss-Bonnet theorem.
with a complex vector bundle V. We let the vector bundles E and F be the sums of the bundles of differential forms with coefficients in V of type (0,i) with i even or odd, and we let the differential operator D be the sum
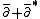
restricted to E. Then the analytical index of D is the holomorphic Euler characteristic of V:
The topological index of D is given by
the product of the Chern character of V and the Todd class of X evaluated on the fundamental class of X.
By equating the topological and analytical indices we get the Hirzebruch–Riemann–Roch theorem. In fact we get a generalization of it to all complex manifolds: Hirzebruch's proof only worked for projective complex manifolds X.
This derivation of the Hirzebruch–Riemann–Roch theorem is more natural if we use the index theorem for elliptic complexes rather than elliptic operators.
We can take the complex to be
with the differential given by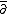
. Then the ith cohomology group is just the coherent cohomology group Hi(X, V), so the analytical index of this complex is the holomorphic Euler characteristic Σ (−1)i dim(Hi(X, V)). As before, the topological index is ch(V)Td(X)[X].
The bundles E and F are given by the +1 and −1 eigenspaces of the operator on the bundle of differential forms of X, that acts on k-forms as
times the Hodge * operator
. The operator D is the Hodge Laplacian
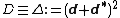
restricted to E, where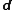
is the Cartan exterior derivative
and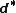
is its adjoint.
The analytic index of D is the signature of the manifold X, and its topological index is the L genus of X, so these are equal.
In dimension 4 this result implies Rochlin's theorem that the signature of a 4 dimensional spin manifold is divisible by 16: this follows because in dimension 4 the  genus is minus one eighth of the signature.
Many proofs of the index theorem use pseudodifferential operators rather than differential operators. The reason for this is that for many purposes there are not enough differential operators. For example, a pseudoinverse of an
elliptic differential operator of positive order is not a differential operator, but is a pseudodifferential operator.
Also, there is a direct correspondence between data representating elements of K(B(X),S(X)) (clutching functions) and symbols of elliptic pseudodifferential operators.
Pseudodifferential operators have an order, which can be any real number or even −∞, and have symbols
(which are no longer polynomials on the cotangent space), and elliptic differential operators are those whose symbols
are invertible for sufficiently large cotangent vectors. Most version of the index theorem can be extended from elliptic differential operators to elliptic pseudodifferential operators.
The idea of this first proof is roughly as follows. Consider the ring generated by pairs (X,V) where V is a smooth vector bundle on the compact smooth oriented manifold X, with relations that the sum and product of the ring on these generators are given by disjoint union and product of manifolds (with the obvious operations on the vector bundles), and any boundary of a manifold with vector bundle is 0. This is similar to the cobordism ring of oriented manifolds, except that the manifolds also have a vector bundle. The topological and analytical indices are both reinterpreted as functions from this ring to the integers. Then one checks that these two functions are in fact both ring homomorphisms. In order to prove they are the same, it is then only necessary to check they are the same on a set of generators of this ring. Thom's cobordism theory gives a set of generators; for example, complex vector spaces with the trivial bundle together with certain bundles over even dimensional spheres. So the index theorem can be proved by checking it on these particularly simple cases.
, described in and . describe a simpler heat equation proof exploiting supersymmetry
.
If D is a differential operator with adjoint D*, then D*D and DD*
are self adjoint operators whose non-zero eigenvalues have the same multiplicities. However their zero eigenspaces may have different multiplicities, as these multiplicities are the dimensions of the kernels of D and D*. Therefore the index of D is given by
for any positive t. The right hand side is given by the trace of the difference of the kernels of two heat operators. These have an asymptotic expansion for small positive t, which can be used to evaluate the limit as t tends to 0, giving a proof of the Atiyah–Singer index theorem.
The asymptotic expansions for small t appear very complicated, but invariant theory shows that there are
huge cancellations between the terms, which makes it possible to find the leading terms explicitly. These cancellations were later explained using supersymmetry.
showed how to extend the index theorem to some non-compact manifolds, acted on by a discrete group with compact quotient. The kernel of the elliptic operator is in general infinite dimensional in this case, but it is possible to get a finite index using the dimension of a module over a von Neumann algebra
; this index is in general real rather than integer valued. This version is called the L2 index theorem, and was used by to rederive properties of the discrete series representation
s of semisimple Lie groups.
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
on a compact manifold, the analytical index (related to the dimension of the space of solutions) is equal to the topological index (defined in terms of some topological data). It includes many other theorems, such as the Riemann–Roch theorem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
, as special cases, and has applications in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
.
History
The index problem for elliptic differential operators was posed by . He noticed the homotopy invariance of the index, and asked for a formula for it by means of topological invariants. Some of the motivating examples included the Riemann–Roch theoremRiemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
and its generalization the Hirzebruch–Riemann–Roch theorem, and the Hirzebruch signature theorem. Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
and Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
had proved the integrality of the  genus of a spin manifold, and Atiyah suggested that this integrality could be explained if it were the index of the Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
(which was rediscovered by Atiyah and Singer in 1961).
The Atiyah–Singer theorem was announced by . The proof sketched in this announcement was never published by them, though it appears in the book . Their first published proof replaced the cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
theory of the first proof with K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, and they used this to give proofs of various generalizations in the papers .
In 1965, S.P. Novikov published his results on the topological invariance of the rational Pontrjagin classes on smooth manifolds.
Kirby and Siebenmann's results , combined with René Thom's paper proved the existence of rational Pontrjagin classes on topological manifolds. The rational Pontrjagin classes are essential ingredients of the index theorem on smooth and topological manifolds.
In 1969, M.F. Atiyah defines abstract elliptic operators on arbitrary metric spaces. Abstract elliptic operators became protagonists in Kasparov's theory and Connes's noncommutative differential geometry.
In 1971, I.M. Singer proposes a comprehensive program for future extensions of index theory.
In 1972, G.G. Kasparov publishes his work on the realization of the K-homology by abstract elliptic operators.
gave a new proof of the index theorem using the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, described in .
In 1977, D. Sullivan establishes his theorem on the existence and uniqueness of Lipschitz and quasiconformal structures on topological manifolds of dimension different from 4.
motivated by ideas of and Alvarez-Gaume, gave a short proof of the local index theorem for operators that are locally Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
s; this covers many of the useful cases.
In 1983, N. Teleman proves that the analytical indices of signature operators with values in vector bundles are topological invariants.
In 1984, N. Teleman establishes the index theorem on topological manifolds.
In 1986, A. Connes publishes his fundamental paper on non-commutative geometry.
In 1989, S.K. Donaldson and D. Sullivan study Yang–Mills theory on quasiconformal manifolds of dimension 4. They introduce the signature operator S defined on differential forms of degree two.
In 1990, A. Connes and H. Moscovici prove the local index formula in the context of non-commutative geometry.
In 1994, A. Connes, D. Sullivan and N. Teleman prove the index theorem for signature operators on quasiconformal manifolds.
Notation
- X is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
smooth manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(without boundary). - E and F are smooth vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s over X. - D is an elliptic differential operator from E to F. So in local coordinates it acts as a differential operator, taking smooth sections of E to smooth sections of F.
The symbol of a differential operator
If D is a differential operator of order n in k variables- x1, ..., xk,
then its symbol
Symbol of a differential operator
In mathematics, the symbol of a linear differential operator associates to a differential operator a polynomial by, roughly speaking, replacing each partial derivative by a new variable. The symbol of a differential operator has broad applications to Fourier analysis. In particular, in this...
is the function of 2k variables
- x1, ... , xk, y1, ..., yk,
given by dropping all terms of order less than n and replacing ∂/∂xi by yi. So the symbol is homogeneous in the variables y, of degree n. The symbol is well defined even though ∂/∂xi does not commute with xi because we only keep the highest order terms and differential operators commute "up to lower-order terms". The operator is called elliptic if the symbol is nonzero whenever at least one y is nonzero.
Example: The Laplace operator in k variables has symbol y12 + ... + yk2, and so is elliptic as this is nonzero whenever any the yis are nonzero. The wave operator has symbol −y12 + ... + yk2, which is not elliptic if k ≥ 2, as the symbol vanishes for some non-zero values of the ys.
The symbol of a differential operator of order n on a smooth manifold X is defined in much the same way using local coordinate charts, and is a function on the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of X, homogeneous of degree n on each cotangent space. (In general, differential operators transform in a rather complicated way under coordinate transforms (see jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
); however, the highest order terms transform like tensors so we get well defined homogeneous functions on the cotangent spaces that are independent of the choice of local charts.) More generally, the symbol of a differential operator between two vector bundles E and F is a section of the pullback of the bundle
- Hom(
to the cotangent space of X. The differential operator is called elliptic if the element of Hom(Ex, Fx) is invertible for all non-zero cotangent vectors at any point x of X.
A key property of elliptic operators is that they are almost invertible; this is closely related to the fact that their symbols are almost invertible. More precisely, an elliptic operator D on a compact manifold has a (non-unique) parametrix
Parametrix
In mathematics, and specifically the field of partial differential equations , a parametrix is an approximation to a fundamental solution of a PDE, and is essentially an approximate inverse to a differential operator....
(or pseudoinverse) D′ such that DD′ − 1 and D′D − 1 are both compact operators. An important consequence is that the kernel of D is finite-dimensional, because all eigenspaces of compact operators, other than the kernel, are finite-dimensional. (The pseudoinverse of an elliptic differential operator is almost never a differential operator. However, it is an elliptic pseudodifferential operator.)
The analytical index
As the elliptic differential operator D has a pseudoinverse, it is a Fredholm operatorFredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
. Any Fredholm operator has an index, defined as the difference between the (finite) dimension of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of D (solutions of Df = 0), and the (finite) dimension of the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of D (the constraints on the right-hand-side of an inhomogeneous equation like Df = g, or equivalently the kernel of the adjoint operator). In other words,
- Index(
This is sometimes called the analytical index of D.
Example. Suppose that the manifold is the circle (thought of as R/Z), and D is the operator d/dx − λ for some complex constant λ. (This is the simplest example of an elliptic operator.) Then the kernel is the space of multiples of exp(λx) if λ is an integral multiple of 2πi and is 0 otherwise, and the kernel of the adjoint is a similar space with λ replaced by its complex conjugate. So D has index 0. This example shows that the kernel and cokernel of elliptic operators can jump discontinuously as the elliptic operator varies, so there is no nice formula for their dimensions in terms of continuous topological data. However the jumps in the dimensions of the kernel and cokernel are the same, so the index, given by the difference of their dimensions, does vary continuously, and can be given in terms of topological data by the index theorem.
The topological index
The topological index of an elliptic differential operator D between smooth vector bundles E and F on an n-dimensional compact manifold X is given by- ch(
in other words the value of the top dimensional component of the mixed cohomology class ch(D)Td(X) on the fundamental homology class of the manifold X.
Here,
- Td(
Todd class
In mathematics, the Todd class is a certain construction now considered a part of the theory in algebraic topology of characteristic classes. The Todd class of a vector bundle can be defined by means of the theory of Chern classes, and is encountered where Chern classes exist — most notably...
of the manifold X.
Another method of defining the topological index uses K theory. If X is a compact submanifold of a manifold Y then there is a pushforward operation from K(TX) to K(TY). The topological index of an element of
K(TX) is defined to be the image of this operation with Y some Euclidean space, for which K(TY) can be naturally identified with the integers Z. This index is independent of the embedding of X in Euclidean space.
The Atiyah–Singer index theorem
As usual, D is an elliptic differential operator between vector bundles E and F over a compact manifold X.The index problem is the following: compute the (analytical) index of D using only the symbol s and topological data derived from the manifold and the vector bundle. The Atiyah–Singer index theorem solves this problem, and states:
- The analytical index of
In spite of its formidable definition, the topological index is usually straightforward to evaluate explicitly. So this makes it possible to evaluate the analytical index. (The cokernel and kernel of an elliptic operator are in general extremely hard to evaluate individually; the index theorem shows that we can usually at least evaluate their difference.) Many important invariants of a manifold (such as the signature) can be given as the index of suitable differential operators, so the index theorem allows us to evaluate these invariants in terms of topological data.
Although the analytical index is usually hard to evaluate directly, it is at least obviously an integer. The topological index is by definition a rational number, but it is usually not at all obvious from the definition that it is also integral. So the Atiyah–Singer index theorem implies some deep integrality properties, as it implies that the topological index is integral.
The index of an elliptic differential operator obviously vanishes if the operator is self adjoint. It also vanishes if the manifold X has odd dimension, though there are pseudodifferential elliptic operators whose index does not vanish in odd dimensions.
Teleman index theorem ,
- For any abstract elliptic operator on a closed, oriented, topological manifold, the analytical index equals the topological index.
The proof of this result goes through specific considerations, including the extension of Hodge theory on combinatorial and Lipschitz manifolds , , the extension of Atiyah–Singer's signature operator to Lipschitz manifolds , Kasparov's K-homology and topological cobordism .
This result shows that the index theorem is not merely a differentiable statement, but rather a topological statement.
Connes–Donaldson–Sullivan–Teleman index theorem ,
- For any quasiconformal manifold there exists a local construction of the Hirzebruch–Thom characteristic classes.
This theory is based on a signature operator S, defined on middle degree differential forms on even-dimensional quasiconformal manifolds (compare ).
Using topological cobordism and K-homology one may provide a full statement of an index theorem on quasiconformal manifolds (see page 678 of ).
The work "provides local constructions for characteristic classes based on higher dimensional relatives of the measurable Riemann mapping in dimension two and the Yang–Mills theory in dimension four."
These results constitute significant advances along the lines of Singer's program Prospects in Mathematics .
At the same time, they provide, also, an effective construction of the rational Pontrjagin classes on topological manifolds.
The paper provides a link between Thom's original construction of the rational Pontrjagin classes and index theory.
It is important to mention that the index formula is a topological statement. The obstruction theories due to Milnor, Kervaire, Kirby, Siebenmann, Sullivan, Donaldson show that only a minority of topological manifolds possess differentiable structures and these are not necessarily unique. Sullivan's result on Lipschitz and quasiconformal structures shows that any topological manifold in dimension different from 4 possesses such a structure which is unique (up to isotopy close to identity).
The quasiconformal structure is the weakest analytical structure on topological manifolds for which the index theorem is known to hold.
The Euler characteristic
Suppose that X is a compact oriented manifold. If we take E to be the sum of the even exterior powers of the cotangent bundle, and F to be the sum of the odd powers, define D to be d + d*, considered as a map from E to F. Then the topological index of D is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the Hodge cohomology of M, and the analytical index is the Euler class of the manifold. The index formula for this operator yields the Chern-Gauss-Bonnet theorem.
Hirzebruch–Riemann–Roch theorem
Take X to be a complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
with a complex vector bundle V. We let the vector bundles E and F be the sums of the bundles of differential forms with coefficients in V of type (0,i) with i even or odd, and we let the differential operator D be the sum
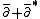
restricted to E. Then the analytical index of D is the holomorphic Euler characteristic of V:
- index(
The topological index of D is given by
- index(
the product of the Chern character of V and the Todd class of X evaluated on the fundamental class of X.
By equating the topological and analytical indices we get the Hirzebruch–Riemann–Roch theorem. In fact we get a generalization of it to all complex manifolds: Hirzebruch's proof only worked for projective complex manifolds X.
This derivation of the Hirzebruch–Riemann–Roch theorem is more natural if we use the index theorem for elliptic complexes rather than elliptic operators.
We can take the complex to be
- 0→
with the differential given by
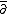. Then the ith cohomology group is just the coherent cohomology group Hi(X, V), so the analytical index of this complex is the holomorphic Euler characteristic Σ (−1)i dim(Hi(X, V)). As before, the topological index is ch(V)Td(X)[X].Hirzebruch signature theorem
The Hirzebruch signature theorem states that the signature of a compact smooth manifold X of dimension 4k is given by the L genus of the manifold. This follows from the Atiyah–Singer index theorem applied to the following signature operator.The bundles E and F are given by the +1 and −1 eigenspaces of the operator on the bundle of differential forms of X, that acts on k-forms as
- i k(k−1)
times the Hodge * operator
Hodge dual
In mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
. The operator D is the Hodge Laplacian
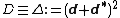
restricted to E, where
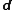is the Cartan exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
and
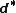is its adjoint.The analytic index of D is the signature of the manifold X, and its topological index is the L genus of X, so these are equal.
The  genus and Rochlin's theorem
The  genus is a rational number defined for any manifold, but is in general not an integer. Borel and Hirzebruch showed that it is integral for spin manifolds, and an even integer if in addition the dimension is 4 mod 8. This can be deduced from the index theorem, which implies that the  genus for spin manifolds is the index of a Dirac operator. The extra factor of 2 in dimensions 4 mod 8 comes from the fact that in this case the kernel and cokernel of the Dirac operator have a quaternionic structure, so as complex vector spaces they have even dimensions, so the index is even.In dimension 4 this result implies Rochlin's theorem that the signature of a 4 dimensional spin manifold is divisible by 16: this follows because in dimension 4 the  genus is minus one eighth of the signature.
Pseudodifferential operators
Pseudodifferential operators can be explained easily in the case of constant coefficient operators on Euclidean space. In this case, constant coefficient differential operators are just the Fourier transforms of multiplication by polynomials, and constant coefficient pseudodifferential operators are just the Fourier transforms of multiplication by more general functions.Many proofs of the index theorem use pseudodifferential operators rather than differential operators. The reason for this is that for many purposes there are not enough differential operators. For example, a pseudoinverse of an
elliptic differential operator of positive order is not a differential operator, but is a pseudodifferential operator.
Also, there is a direct correspondence between data representating elements of K(B(X),S(X)) (clutching functions) and symbols of elliptic pseudodifferential operators.
Pseudodifferential operators have an order, which can be any real number or even −∞, and have symbols
(which are no longer polynomials on the cotangent space), and elliptic differential operators are those whose symbols
are invertible for sufficiently large cotangent vectors. Most version of the index theorem can be extended from elliptic differential operators to elliptic pseudodifferential operators.
Cobordism
The initial proof was based on that of the Hirzebruch–Riemann–Roch theorem (1954), and involved cobordism theory and pseudodifferential operators.The idea of this first proof is roughly as follows. Consider the ring generated by pairs (X,V) where V is a smooth vector bundle on the compact smooth oriented manifold X, with relations that the sum and product of the ring on these generators are given by disjoint union and product of manifolds (with the obvious operations on the vector bundles), and any boundary of a manifold with vector bundle is 0. This is similar to the cobordism ring of oriented manifolds, except that the manifolds also have a vector bundle. The topological and analytical indices are both reinterpreted as functions from this ring to the integers. Then one checks that these two functions are in fact both ring homomorphisms. In order to prove they are the same, it is then only necessary to check they are the same on a set of generators of this ring. Thom's cobordism theory gives a set of generators; for example, complex vector spaces with the trivial bundle together with certain bundles over even dimensional spheres. So the index theorem can be proved by checking it on these particularly simple cases.
K theory
Atiyah and Singer's first published proof used K theory rather than cobordism. If i is any inclusion of compact manifolds from X to Y, they defined a 'pushforward' operation i! on elliptic operators of X to elliptic operators of Y that preserves the index. By taking Y to be some sphere that X embeds in, this reduces the index theorem to the case of spheres. If Y is a sphere and X is some point embedded in Y, then any elliptic operator on Y is the image under i! of some elliptic operator on the point. This reduces the index theorem to the case of a point, when it is trivial.Heat equation
gave a new proof of the index theorem using the heat equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, described in and . describe a simpler heat equation proof exploiting supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
.
If D is a differential operator with adjoint D*, then D*D and DD*
are self adjoint operators whose non-zero eigenvalues have the same multiplicities. However their zero eigenspaces may have different multiplicities, as these multiplicities are the dimensions of the kernels of D and D*. Therefore the index of D is given by
- Index(D) = dim Ker(D) − dim Ker(D*) = Tr(e−t D*D) − Tr(e−t DD*)
for any positive t. The right hand side is given by the trace of the difference of the kernels of two heat operators. These have an asymptotic expansion for small positive t, which can be used to evaluate the limit as t tends to 0, giving a proof of the Atiyah–Singer index theorem.
The asymptotic expansions for small t appear very complicated, but invariant theory shows that there are
huge cancellations between the terms, which makes it possible to find the leading terms explicitly. These cancellations were later explained using supersymmetry.
Generalizations
- The Atiyah–Singer theorem applies to elliptic pseudodifferential operators in much the same way as for elliptic differential operators. In fact, for technical reasons most of the early proofs worked with pseudodifferential rather than differential operators: their extra flexibility made some steps of the proofs easier.
- Instead of working with an elliptic operator between two vector bundles, it is sometimes more convenient to work with an elliptic complexElliptic complexIn mathematics, in particular in partial differential equations and differential geometry, an elliptic complex generalizes the notion of an elliptic operator to sequences. Elliptic complexes isolate those features common to the de Rham complex and the Dolbeault complex which are essential for...
-
- 0 → E0 → E1 →E2 → ... → Em →0
- of vector bundles. The difference is that the symbols now form an exact sequence (off the zero section). In the case when there are just two non-zero bundles in the complex this implies that the symbol is an isomorphism off the zero section, so an elliptic complex with 2 terms is essentially the same as an elliptic operator between two vector bundles. Conversely the index theorem for an elliptic complex can easily be reduced to the case of an elliptic operator: the two vector bundles are given by the sums of the even or odd terms of the complex, and the elliptic operator is the sum of the operators of the elliptic complex and their adjoints, restricted to the sum of the even bundles.
- If the manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is allowed to have boundary, then some restrictions must be put on the domain of the elliptic operator in order to ensure a finite index. These conditions can be local (like demanding that the sections in the domain vanish at the boundary) or more complicated global conditions (like requiring that the sections in the domain solve some differential equation). The local case was worked out by Atiyah and Bott, but they showed that many interesting operators (e.g., the signature operatorSignature operatorIn mathematics, the signature operator is an elliptic differential operator defined on a certain subspace of the space of differential forms on an even-dimensional compact Riemannian manifold, whose analytic index is the same as the topological signature of the manifold if the dimension of the...
) do not admit local boundary conditions. To handle these operators, AtiyahMichael AtiyahSir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
, PatodiVijay Kumar PatodiVijay Kumar Patodi was an Indian mathematician who made fundamental contributions to differential geometry and topology. He was the first mathematician to apply heat equation methods to the proof of the Index Theorem for elliptic operators...
and SingerIsadore SingerIsadore Manuel Singer is an Institute Professor in the Department of Mathematics at the Massachusetts Institute of Technology...
introduced global boundary conditions equivalent to attaching a cylinder to the manifold along the boundary and then restricting the domain to those sections that are square integrable along the cylinder. This point of view is adopted in the proof of of the Atiyah–Patodi–Singer index theorem.
- Instead of just one elliptic operator, one can consider a family of elliptic operators parameterized by some space Y. In this case the index is an element of the K-theory of Y, rather than an integer. If the operators in the family are real, then the index lies in the real K-theory of Y. This gives a little extra information, as the map from the real K theory of Y to the complex K theory is not always injective.
- If there is a group actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a group G on the compact manifold X, commuting with the elliptic operator, then one replaces ordinary K theory with equivariant K-theory. Moreover, one gets generalizations of the Lefschetz fixed point theorem, with terms coming from fixed point submanifolds of the group G.
showed how to extend the index theorem to some non-compact manifolds, acted on by a discrete group with compact quotient. The kernel of the elliptic operator is in general infinite dimensional in this case, but it is possible to get a finite index using the dimension of a module over a von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
; this index is in general real rather than integer valued. This version is called the L2 index theorem, and was used by to rederive properties of the discrete series representation
Discrete series representation
In mathematics, a discrete series representation is an irreducible unitary representation of a locally compact topological group G that is a subrepresentation of the left regular representation of G on L²...
s of semisimple Lie groups.
- The Callias index theorem is an index theorem for a Dirac operator on a noncompact odd-dimensional space. The Atiyah–Singer index is only defined on compact spaces, and vanishes when their dimension is odd. In 1978 Constantine Callias, at the suggestion of his Ph.D. advisor Roman JackiwRoman JackiwRoman W. Jackiw is a theoretical physicist and Dirac Medallist. Born in Poland, Jackiw received his PhD from Cornell University in 1966 under Hans Bethe and Kenneth Wilson...
, used the axial anomalyChiral anomalyA chiral anomaly is the anomalous nonconservation of a chiral current. In some theories of fermions with chiral symmetry, the quantization may lead to the breaking of this chiral symmetry. In that case, the charge associated with the chiral symmetry is not conserved.The non-conservation happens...
to derive this index theorem on spaces equipped with a Hermitian matrix called the Higgs field. As presented in his paper Index Theorems on Open Spaces the index of the Dirac operator is a topological invariant which measures the winding of the Higgs field on a sphere at infinity. If
is the unit matrix in the direction of the Higgs field, then the index is proportional to the integral of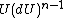 
over the (n − 1)-sphere at infinity. If n is even, it is always zero. The topological interpretation of this invariant and its relation to the Hörmander index proposed by Boris Fedosov, as generalized by Lars HörmanderLars HörmanderLars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
, was published by Raoul BottRaoul BottRaoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
and Robert Thomas Seeley in the article Some Remarks on the Paper of Callias in the same issue of Communications in Mathematical PhysicsCommunications in Mathematical PhysicsCommunications in Mathematical Physics is a peer-reviewed academic journal published by Springer. The journal publishes papers in all fields of mathematical physics, but focuses particularly in Analysis related to condensed matter physics, statistical mechanics and quantum field theory, and in...
as Callias' article.
External links
- Rafe Mazzeo: The Atiyah–Singer Index Theorem: What it is and why you should care. Pdf presentation.
- Raussen, Skau, Interview with Atiyah, Singer, Notices AMS 2005.
- R. R. Seeley and other, Recollections from the early days of index theory and pseudo-differential operators
- A. J. Wassermann, Lecture notes on the Atiyah–Singer Index Theorem