
Spectral theorem
Encyclopedia
In mathematics
, particularly linear algebra
and functional analysis
, the spectral theorem is any of a number of results about linear operators or about matrices
. In broad terms the spectral theorem
provides conditions under which an operator or a matrix can be diagonalized
(that is, represented as a diagonal matrix
in some basis). This concept of diagonalization is relatively straightforward for operators on finite-dimensional spaces, but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modelled by multiplication operator
s, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory
for a historical perspective.
Examples of operators to which the spectral theorem applies are self-adjoint operator
s or more generally normal operator
s on Hilbert space
s.
The spectral theorem also provides a canonical decomposition, called the spectral decomposition, eigenvalue decomposition, or eigendecomposition
, of the underlying vector space on which the operator acts.
In this article we consider mainly the simplest kind of spectral theorem, that for a self-adjoint
operator on a Hilbert space. However, as noted above, the spectral theorem also holds for normal operators on a Hilbert space.
or complex
inner product space
V with the standard Hermitian inner product; the Hermitian condition means
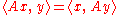
for all elements x and y of V.
An equivalent condition is that A* = A, where A* is the conjugate transpose
of A. If A is a real matrix, this is equivalent to AT = A (that is, A is a symmetric matrix).
This condition easily implies that all eigenvalues of a Hermitian matrix are real: it is enough to apply it to the case when x=y is an eigenvector.
(Recall that an eigenvector of a linear operator A is a (non-zero) vector x such that Ax = λx for some scalar λ. The value λ is the corresponding eigenvalue.)
Theorem. There is an orthonormal basis
of V consisting of eigenvectors of A. Each eigenvalue is real.
We provide a sketch of a proof for the case where the underlying field of scalars is the complex number
s.
By the fundamental theorem of algebra
, applied to the characteristic polynomial, any square matrix with complex entries has at least one eigenvector. Now if A is Hermitian with eigenvector e1, we can consider the space K = span{e1}⊥, the orthogonal complement of e1. By Hermiticity, K is an invariant subspace
of A. Applying the same argument to K shows that A has an eigenvector e2 ∈ K. Finite induction then finishes the proof.
The spectral theorem holds also for symmetric matrices on finite-dimensional real inner product spaces, but the existence of an eigenvector does not follow immediately from the fundamental theorem of algebra
. The easiest way to prove it is probably to consider A as a Hermitian matrix and use the fact that all eigenvalues of a Hermitian matrix are real.
If one chooses the eigenvectors of A as an orthonormal basis, the matrix representation of A in this basis is diagonal. Equivalently, A can be written as a linear combination of pairwise orthogonal projections, called its spectral decomposition. Let

be the eigenspace corresponding to an eigenvalue λ. Note that the definition does not depend on any choice of specific eigenvectors. V is the orthogonal direct sum of the spaces Vλ where the index ranges over eigenvalues. Let Pλ be the orthogonal projection onto Vλ and λ1, ..., λm the eigenvalues of A, one can write its spectral decomposition thus:

The spectral decomposition is a special case of the Schur decomposition
. It is also a special case of the singular value decomposition
.
For the infinite-dimensional case, A is a linear operator, and the spectral decomposition is given by the integral
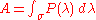
where σ is the spectrum of A and P is a projection (i.e. idempotent) operator.
if A* A = A A*. One can show that A is normal if and only if it is unitarily diagonalizable: By the Schur decomposition
, we have A = U T U*, where U is unitary and T upper-triangular.
Since A is normal, T T* = T* T. Therefore T must be diagonal since normal upper triangular matrices are diagonal . The converse is also obvious.
In other words, A is normal if and only if there exists a unitary matrix U such that
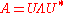
where Λ is the diagonal matrix
the entries of which are the eigenvalues of A. The column vectors of U are the eigenvectors of A and they are orthonormal. Unlike the Hermitian case, the entries of Λ need not be real.
self-adjoint operators is virtually the same as in the finite-dimensional case.
Theorem. Suppose A is a compact self-adjoint operator on a Hilbert space V. There is an orthonormal basis
of V consisting of eigenvectors of A. Each eigenvalue is real.
As for Hermitian matrices, the key point is to prove the existence of at least one nonzero eigenvector. To prove this, we cannot rely on determinants to show existence of eigenvalues, but instead one can use a maximization argument analogous to the variational characterization of eigenvalues. The above spectral theorem holds for real or complex Hilbert spaces.
If the compactness assumption is removed, it is not true that every self adjoint operator has eigenvectors.
self-adjoint operators on a Hilbert space. Such operators may have no eigenvalues: for instance let A be the operator of multiplication by t on L2[0, 1], that is
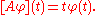
Theorem. Let A be a bounded self-adjoint operator on a Hilbert space H. Then there is a measure space (X, Σ, μ) and a real-valued measurable function f on X and a unitary operator U:H → L2μ(X) such that

where T is the multiplication operator
:
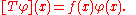
This is the beginning of the vast research area of functional analysis called operator theory
.
There is also an analogous spectral theorem for bounded normal operator
s on Hilbert spaces. The only difference in the conclusion is that now may be complex-valued.
may be complex-valued.
An alternative formulation of the spectral theorem expresses the operator as an integral of the coordinate function over the operator's spectrum with respect to a projection-valued measure
as an integral of the coordinate function over the operator's spectrum with respect to a projection-valued measure
. When the normal operator in question is compact
, this version of the spectral theorem reduces to the finite-dimensional spectral theorem above, except that the operator is expressed as a linear combination of possibly infinitely many projections.
, such as differential operators, are unbounded. There is also a spectral theorem for self-adjoint operator
s that applies in these cases. To give an example, any constant coefficient differential operator is unitarily equivalent to a multiplication operator. Indeed the unitary operator that implements this equivalence is the Fourier transform
; the multiplication operator is a type of Fourier multiplier
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the spectral theorem is any of a number of results about linear operators or about matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. In broad terms the spectral theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
provides conditions under which an operator or a matrix can be diagonalized
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
(that is, represented as a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
in some basis). This concept of diagonalization is relatively straightforward for operators on finite-dimensional spaces, but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modelled by multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
s, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
for a historical perspective.
Examples of operators to which the spectral theorem applies are self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s or more generally normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.
The spectral theorem also provides a canonical decomposition, called the spectral decomposition, eigenvalue decomposition, or eigendecomposition
Eigendecomposition of a matrix
In the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...
, of the underlying vector space on which the operator acts.
In this article we consider mainly the simplest kind of spectral theorem, that for a self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
operator on a Hilbert space. However, as noted above, the spectral theorem also holds for normal operators on a Hilbert space.
Hermitian matrices
We begin by considering a Hermitian matrix A on a finite-dimensional realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
V with the standard Hermitian inner product; the Hermitian condition means
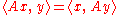
for all elements x and y of V.
An equivalent condition is that A* = A, where A* is the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A. If A is a real matrix, this is equivalent to AT = A (that is, A is a symmetric matrix).
This condition easily implies that all eigenvalues of a Hermitian matrix are real: it is enough to apply it to the case when x=y is an eigenvector.
(Recall that an eigenvector of a linear operator A is a (non-zero) vector x such that Ax = λx for some scalar λ. The value λ is the corresponding eigenvalue.)
Theorem. There is an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of V consisting of eigenvectors of A. Each eigenvalue is real.
We provide a sketch of a proof for the case where the underlying field of scalars is the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
By the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
, applied to the characteristic polynomial, any square matrix with complex entries has at least one eigenvector. Now if A is Hermitian with eigenvector e1, we can consider the space K = span{e1}⊥, the orthogonal complement of e1. By Hermiticity, K is an invariant subspace
Invariant subspace
In mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
of A. Applying the same argument to K shows that A has an eigenvector e2 ∈ K. Finite induction then finishes the proof.
The spectral theorem holds also for symmetric matrices on finite-dimensional real inner product spaces, but the existence of an eigenvector does not follow immediately from the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
. The easiest way to prove it is probably to consider A as a Hermitian matrix and use the fact that all eigenvalues of a Hermitian matrix are real.
If one chooses the eigenvectors of A as an orthonormal basis, the matrix representation of A in this basis is diagonal. Equivalently, A can be written as a linear combination of pairwise orthogonal projections, called its spectral decomposition. Let

be the eigenspace corresponding to an eigenvalue λ. Note that the definition does not depend on any choice of specific eigenvectors. V is the orthogonal direct sum of the spaces Vλ where the index ranges over eigenvalues. Let Pλ be the orthogonal projection onto Vλ and λ1, ..., λm the eigenvalues of A, one can write its spectral decomposition thus:

The spectral decomposition is a special case of the Schur decomposition
Schur decomposition
In the mathematical discipline of linear algebra, the Schur decomposition or Schur triangulation, named after Issai Schur, is a matrix decomposition.- Statement :...
. It is also a special case of the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
.
For the infinite-dimensional case, A is a linear operator, and the spectral decomposition is given by the integral
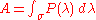
where σ is the spectrum of A and P is a projection (i.e. idempotent) operator.
Normal matrices
The spectral theorem extends to a more general class of matrices. Let A be an operator on a finite-dimensional inner product space. A is said to be normalNormal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
if A* A = A A*. One can show that A is normal if and only if it is unitarily diagonalizable: By the Schur decomposition
Schur decomposition
In the mathematical discipline of linear algebra, the Schur decomposition or Schur triangulation, named after Issai Schur, is a matrix decomposition.- Statement :...
, we have A = U T U*, where U is unitary and T upper-triangular.
Since A is normal, T T* = T* T. Therefore T must be diagonal since normal upper triangular matrices are diagonal . The converse is also obvious.
In other words, A is normal if and only if there exists a unitary matrix U such that
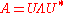
where Λ is the diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
the entries of which are the eigenvalues of A. The column vectors of U are the eigenvectors of A and they are orthonormal. Unlike the Hermitian case, the entries of Λ need not be real.
Compact self-adjoint operators
In Hilbert spaces in general, the statement of the spectral theorem for compactCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
self-adjoint operators is virtually the same as in the finite-dimensional case.
Theorem. Suppose A is a compact self-adjoint operator on a Hilbert space V. There is an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of V consisting of eigenvectors of A. Each eigenvalue is real.
As for Hermitian matrices, the key point is to prove the existence of at least one nonzero eigenvector. To prove this, we cannot rely on determinants to show existence of eigenvalues, but instead one can use a maximization argument analogous to the variational characterization of eigenvalues. The above spectral theorem holds for real or complex Hilbert spaces.
If the compactness assumption is removed, it is not true that every self adjoint operator has eigenvectors.
Bounded self-adjoint operators
The next generalization we consider is that of boundedBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
self-adjoint operators on a Hilbert space. Such operators may have no eigenvalues: for instance let A be the operator of multiplication by t on L2[0, 1], that is
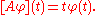
Theorem. Let A be a bounded self-adjoint operator on a Hilbert space H. Then there is a measure space (X, Σ, μ) and a real-valued measurable function f on X and a unitary operator U:H → L2μ(X) such that

where T is the multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
:
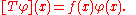
This is the beginning of the vast research area of functional analysis called operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
.
There is also an analogous spectral theorem for bounded normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s on Hilbert spaces. The only difference in the conclusion is that now
 may be complex-valued.
may be complex-valued.An alternative formulation of the spectral theorem expresses the operator
 as an integral of the coordinate function over the operator's spectrum with respect to a projection-valued measure
as an integral of the coordinate function over the operator's spectrum with respect to a projection-valued measureProjection-valued measure
In mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
. When the normal operator in question is compact
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
, this version of the spectral theorem reduces to the finite-dimensional spectral theorem above, except that the operator is expressed as a linear combination of possibly infinitely many projections.
General self-adjoint operators
Many important linear operators which occur in analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, such as differential operators, are unbounded. There is also a spectral theorem for self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s that applies in these cases. To give an example, any constant coefficient differential operator is unitarily equivalent to a multiplication operator. Indeed the unitary operator that implements this equivalence is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
; the multiplication operator is a type of Fourier multiplier
Multiplier (Fourier analysis)
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol...
.
See also
- Spectral theorySpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
- Matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
- Canonical formCanonical formGenerally, in mathematics, a canonical form of an object is a standard way of presenting that object....
- Jordan decompositionJordan normal formIn linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
, of which the spectral decomposition is a special case. - Singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
, a generalisation of spectral theorem to arbitrary matrices. - Eigendecomposition of a matrixEigendecomposition of a matrixIn the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...

