Coefficient
Encyclopedia
In mathematics
, a coefficient is a multiplicative factor in some term
of an expression
(or of a series
); it is usually a number, but in any case does not involve any variable
s of the expression. For instance in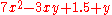
the first three terms respectively have the coefficients 7, −3, and 1.5 (in the third term the variables are hidden (raised to the 0 power), so the coefficient is the term itself; it is called the constant term
or constant coefficient of this expression). The final term does not have any explicitly written coefficient, but is considered to have coefficient 1, since multiplying by that factor would not change the term. Often coefficients are numbers as in this example, although they could be parameters of the problem, as a, b, and c in
when it is understood that these are not considered as variables.
Thus a polynomial
in one variable x can be written as
for some integer k, where ak, ... a1, a0 are coefficients; to allow this kind of expression in all cases one must allow introducing terms with 0 as coefficient.
For the largest i with (if any), ai is called the leading coefficient of the polynomial. So for example the leading coefficient of the polynomial
is 4.
Specific coefficients arise in mathematical identities, such as the binomial theorem
which involves binomial coefficient
s; these particular coefficients are tabulated in Pascal's triangle
.
, the leading coefficient of a row in a matrix is the first nonzero entry in that row. So, for example, given
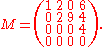
The leading coefficient of the first row is 1; 2 is the leading coefficient of the second row; 4 is the leading coefficient of the third row, and the last row does not have a leading coefficient.
Though coefficients are frequently viewed as constants
in elementary algebra, they can be variables more generally. For example, the coordinates
of a vector v in a vector space
with basis
, are the coefficients of the basis vectors in the expression
Coefficient is just the fancy name for the numbers multiplied by variables.
to indicate how many molecules
(or atoms) take part in the reaction. For example, in the formula
, the number 2's in front of 
and 
are stoichiometric coefficients
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a coefficient is a multiplicative factor in some term
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
of an expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
(or of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
); it is usually a number, but in any case does not involve any variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s of the expression. For instance in
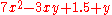
the first three terms respectively have the coefficients 7, −3, and 1.5 (in the third term the variables are hidden (raised to the 0 power), so the coefficient is the term itself; it is called the constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
or constant coefficient of this expression). The final term does not have any explicitly written coefficient, but is considered to have coefficient 1, since multiplying by that factor would not change the term. Often coefficients are numbers as in this example, although they could be parameters of the problem, as a, b, and c in
when it is understood that these are not considered as variables.
Thus a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in one variable x can be written as
for some integer k, where ak, ... a1, a0 are coefficients; to allow this kind of expression in all cases one must allow introducing terms with 0 as coefficient.
For the largest i with (if any), ai is called the leading coefficient of the polynomial. So for example the leading coefficient of the polynomial
is 4.
Specific coefficients arise in mathematical identities, such as the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
which involves binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s; these particular coefficients are tabulated in Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
Linear algebra
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the leading coefficient of a row in a matrix is the first nonzero entry in that row. So, for example, given
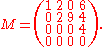
The leading coefficient of the first row is 1; 2 is the leading coefficient of the second row; 4 is the leading coefficient of the third row, and the last row does not have a leading coefficient.
Though coefficients are frequently viewed as constants
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
in elementary algebra, they can be variables more generally. For example, the coordinates
of a vector v in a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, are the coefficients of the basis vectors in the expressionCoefficient is just the fancy name for the numbers multiplied by variables.
Examples of physical coefficients
- Coefficient of Thermal Expansion (thermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
) (dimensionless) - Relates the change in temperature to the change in a material's dimensions. - Partition CoefficientPartition coefficientIn chemistry and the pharmaceutical sciences, a partition- or distribution coefficient is the ratio of concentrations of a compound in the two phases of a mixture of two immiscible solvents at equilibrium. The terms "gas/liquid partition coefficient" and "air/water partition coefficient" are...
(KD) (chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
) - The ratio of concentrations of a compound in two phases of a mixture of two immiscible solvents at equilibrium. - Hall coefficientHall effectThe Hall effect is the production of a voltage difference across an electrical conductor, transverse to an electric current in the conductor and a magnetic field perpendicular to the current...
(electrical physics) - Relates a magnetic field applied to an element to the voltage created, the amount of current and the element thickness. It is a characteristic of the material from which the conductor is made. - Lift coefficientLift coefficientThe lift coefficient is a dimensionless coefficient that relates the lift generated by a lifting body, the dynamic pressure of the fluid flow around the body, and a reference area associated with the body...
(CL or CZ) (AerodynamicsAerodynamicsAerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
) (dimensionless) - Relates the lift generated by an airfoil with the dynamic pressure of the fluid flow around the airfoil, and the planform area of the airfoil. - Ballistic coefficientBallistic coefficientIn ballistics, the ballistic coefficient of a body is a measure of its ability to overcome air resistance in flight. It is inversely proportional to the negative acceleration—a high number indicates a low negative acceleration. BC is a function of mass, diameter, and drag coefficient...
(BC) (AerodynamicsAerodynamicsAerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
) (units of kg/m2) - A measure of a body's ability to overcome air resistance in flight. BC is a function of mass, diameter, and drag coefficient. - Transmission Coefficient (quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
) (dimensionless) - Represents the probability flux of a transmitted wave relative to that of an incident wave. It is often used to describe the probability of a particle tunnellingQuantum tunnellingQuantum tunnelling refers to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important...
through a barrier. - Damping FactorDampingIn physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
a.k.a. viscous damping coefficient (Physical Engineering) (units of newton-seconds per meter) - relates a damping force with the velocity of the object whose motion is being
Chemistry
A coefficient is a number placed in front of a term in a chemical equationChemical equation
A chemical equation is the symbolic representation of a chemical reaction where the reactant entities are given on the left hand side and the product entities on the right hand side. The coefficients next to the symbols and formulae of entities are the absolute values of the stoichiometric numbers...
to indicate how many molecules
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
(or atoms) take part in the reaction. For example, in the formula
, the number 2's in front of and are stoichiometric coefficientsStoichiometry
Stoichiometry is a branch of chemistry that deals with the relative quantities of reactants and products in chemical reactions. In a balanced chemical reaction, the relations among quantities of reactants and products typically form a ratio of whole numbers...
.