
Superposition principle
Overview
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and systems theory
Systems theory
Systems theory is the transdisciplinary study of systems in general, with the goal of elucidating principles that can be applied to all types of systems at all nesting levels in all fields of research...
, the superposition principle , also known as superposition property, states that, for all linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually. So that if input A produces response X and input B produces response Y then input (A + B) produces response (X + Y).
Mathematically, for a linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
, F, defined by F(x) = y, where x is some sort of stimulus (input) and y is some sort of response (output), the superposition (i.e., sum) of stimuli yields a superposition of the respective responses:
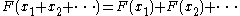 .
.The superposition principle holds because, by definition, a linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
must be additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
.
Discussions

