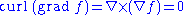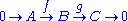
Exact sequence
Encyclopedia
An exact sequence is a concept in mathematics
, especially in homological algebra
and other applications of abelian category
theory, as well as in differential geometry and group theory
. An exact sequence is a sequence
, either finite or infinite, of objects and morphism
s between them such that the image
of one morphism equals the kernel of the next.
, a sequence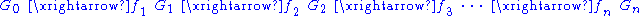
of groups
and group homomorphism
s is called exact if the image
(or range
) of each homomorphism is equal to the kernel
of the next:
Note that the sequence of groups and homomorphisms may be either finite or infinite.
A similar definition can be made for certain other algebraic structure
s. For example, one could have an exact sequence of vector space
s and linear maps, or of modules
and module homomorphisms. More generally, the notion of an exact sequence makes sense in any category
with kernel
s and cokernel
s.
where ƒ is a monomorphism
and g is an epimorphism
. In this case, A is essentially a subobject
of B, and the corresponding quotient
is isomorphic
to C:
(where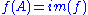
).
A short exact sequence of abelian groups may also be written as an exact sequence with five terms: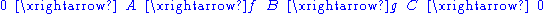
where 0 represents the zero object, such as the trivial group
or a zero-dimensional vector space. The placement of the 0's forces ƒ to be a monomorphism and g to be an epimorphism (see below).
If instead the objects are groups not known to be abelian, then multiplicative rather than additive notation is traditional, and the identity element -- as well as the trivial group -- is often written as "1" instead of "0". So in that case a short exact sequence would be written as follows: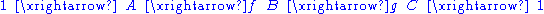
s:
The first operation forms an element in the set of integers,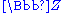
, using multiplication by 2 on an element from 
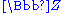j=2i. The second operation forms an element in the quotient space, j=i mod 2.
Here the hook arrow
indicates that the map 
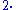from Z to Z is a monomorphism
, and the two-headed arrow
indicates an epimorphism
(the map mod 2). This is an exact sequence because the image 2Z of the monomorphism is the kernel of the epimorphism.
This sequence may also be written without using special symbols for monomorphism and epimorphism: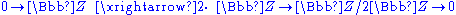
Here 0 denotes the trivial abelian group with a single element, the map from Z to Z is multiplication by 2, and the map from Z to the factor group Z/2Z is given by reducing integers modulo
2. This is indeed an exact sequence:
Another example, from differential geometry, especially relevant for work on the Maxwell equations:
,
based on the fact that on properly defined Hilbert space
s,
in addition, curl
-free vector fields can always be written as a gradient of a scalar function, and that a divergence
less field can be written as a curl of another field.
Note 1: this example makes use of the fact that 3-dimensional space is topologically trivial.
Note 2: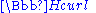
and 
are the domains for the 
and 
operators respectively.
Important are short exact sequences, which are exact sequences of the form
By the above, we know that for any such short exact sequence, f is a monomorphism and g is an epimorphism. Furthermore, the image of f is equal to the kernel of g. It is helpful to think of A as a subobject of B with f being the embedding of A into B, and of C as the corresponding factor object B/A, with the map g being the natural projection from B to B/A (whose kernel is exactly A).
states that if the above short exact sequence admits a morphism t: B → A such that t o f is the identity on A or
a morphism u: C → B such that g o u is the identity on C, then B is a twisted direct sum of A and C.
(For groups, a twisted direct sum is a semidirect product
; in an abelian category, every twisted direct sum is an ordinary direct sum
.)
In this case, we say that the short exact sequence splits.
The snake lemma
shows how a commutative diagram
with two exact rows gives rise to a longer exact sequence. The nine lemma
is a special case.
The five lemma
gives conditions under which the middle map in a commutative diagram with exact rows of length 5 is an isomorphism; the short five lemma
is a special case thereof applying to short exact sequences.
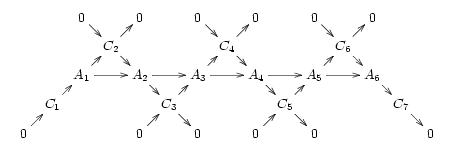
The importance of short exact sequences is underlined by the fact that every exact sequence results from "weaving together" several overlapping short exact sequences. Consider for instance the exact sequence
,
which implies that there exist objects
in the category such that
.
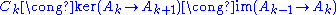Suppose in addition that the cokernel
of each morphism exists, and is isomorphic to the image of the next morphism in the sequence:
(This is true for a number of interesting categories, including any abelian category such as the abelian group
s; but it is not true for all categories that allow exact sequences, and in particular is not true for the category of groups
, in which
is not 
but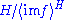 
, the quotient of H by the conjugate closure
of
.) Then we obtain a commutative diagram in which all the diagonals are short exact sequences:
Note that the only portion of this diagram that depends on the cokernel condition is the object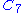
and the final pair of morphisms 
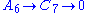. If there exists any object 
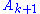and morphism 
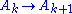such that 
is exact, then the exactness of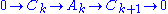 
is ensured. Again taking the example of the category of groups, the fact that 
is the kernel of some homomorphism on H implies that it is a normal subgroup
, which coincides with its conjugate closure; thus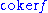
is isomorphic to the image 
of the next morphism.
Conversely, given any list of overlapping short exact sequences, their middle terms form an exact sequence in the same manner.
The extension problem is essentially the question "Given the end terms A and C of a short exact sequence, what possibilities exist for the middle term B?" In the category of groups, this is equivalent to the question, what groups B have A as a normal subgroup
and C as the corresponding factor group? This problem is important in the classification of groups
. See also Outer automorphism group
.
Notice that in an exact sequence, the composition fi+1 o fi maps Ai to 0 in Ai+2, so every exact sequence is a chain complex
.
Furthermore, only fi-images of elements of Ai are mapped to 0 by fi+1, so the homology
of this chain complex is trivial. More succinctly:
Given any chain complex, its homology can therefore be thought of as a measure of the degree to which it fails to be exact.
If we take a series of short exact sequences linked by chain complexes (that is, a short exact sequence of chain complexes, or from another point of view, a chain complex of short exact sequences), then we can derive from this a long exact sequence (i.e. an exact sequence indexed by the natural numbers) on homology by application of the zig-zag lemma
. It comes up in algebraic topology
in the study of relative homology
; the Mayer–Vietoris sequence is another example. Long exact sequences induced by short exact sequences are also characteristic of derived functor
s.
Exact functor
s are functor
s that transform exact sequences into exact sequences.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and other applications of abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
theory, as well as in differential geometry and group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. An exact sequence is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
, either finite or infinite, of objects and morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s between them such that the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of one morphism equals the kernel of the next.
Definition
In the context of group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a sequence
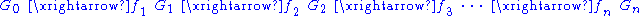
of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s is called exact if the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
(or range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
) of each homomorphism is equal to the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the next:
Note that the sequence of groups and homomorphisms may be either finite or infinite.
A similar definition can be made for certain other algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s. For example, one could have an exact sequence of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and linear maps, or of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and module homomorphisms. More generally, the notion of an exact sequence makes sense in any category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
s and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
s.
Short exact sequence
The most common type of exact sequence is the short exact sequence. This is an exact sequence of the formwhere ƒ is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
and g is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
. In this case, A is essentially a subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
of B, and the corresponding quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to C:
(where
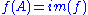).A short exact sequence of abelian groups may also be written as an exact sequence with five terms:
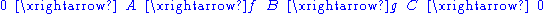
where 0 represents the zero object, such as the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
or a zero-dimensional vector space. The placement of the 0's forces ƒ to be a monomorphism and g to be an epimorphism (see below).
If instead the objects are groups not known to be abelian, then multiplicative rather than additive notation is traditional, and the identity element -- as well as the trivial group -- is often written as "1" instead of "0". So in that case a short exact sequence would be written as follows:
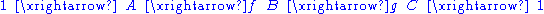
Example
Consider the following sequence of abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s:
The first operation forms an element in the set of integers,
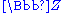, using multiplication by 2 on an element from 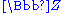j=2i. The second operation forms an element in the quotient space, j=i mod 2.Here the hook arrow
indicates that the map from Z to Z is a monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, and the two-headed arrow
indicates an epimorphismEpimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
(the map mod 2). This is an exact sequence because the image 2Z of the monomorphism is the kernel of the epimorphism.
This sequence may also be written without using special symbols for monomorphism and epimorphism:
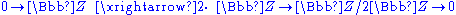
Here 0 denotes the trivial abelian group with a single element, the map from Z to Z is multiplication by 2, and the map from Z to the factor group Z/2Z is given by reducing integers modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
2. This is indeed an exact sequence:
- the image of the map 0→Z is {0}, and the kernel of multiplication by 2 is also {0}, so the sequence is exact at the first Z.
- the image of multiplication by 2 is 2Z, and the kernel of reducing modulo 2 is also 2Z, so the sequence is exact at the second Z.
- the image of reducing modulo 2 is all of Z/2Z, and the kernel of the zero map is also all of Z/2Z, so the sequence is exact at the position Z/2Z
Another example, from differential geometry, especially relevant for work on the Maxwell equations:
,based on the fact that on properly defined Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s,
in addition, curl
Curl
In vector calculus, the curl is a vector operator that describes the infinitesimal rotation of a 3-dimensional vector field. At every point in the field, the curl is represented by a vector...
-free vector fields can always be written as a gradient of a scalar function, and that a divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
less field can be written as a curl of another field.
Note 1: this example makes use of the fact that 3-dimensional space is topologically trivial.
Note 2:
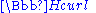and are the domains for the and operators respectively.Special cases
To make sense of the definition, it is helpful to consider what it means in relatively simple cases where the sequence is finite and begins or ends with 0.- The sequence 0 → A → B is exact at A if and only if the map from A to B has kernel {0}, i.e. if and only if that map is a monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
(one-to-one). - Dually, the sequence B → C → 0 is exact at C if and only if the image of the map from B to C is all of C, i.e. if and only if that map is an epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
(onto). - A consequence of these last two facts is that the sequence 0 → X → Y → 0 is exact if and only if the map from X to Y is an isomorphism.
Important are short exact sequences, which are exact sequences of the form
By the above, we know that for any such short exact sequence, f is a monomorphism and g is an epimorphism. Furthermore, the image of f is equal to the kernel of g. It is helpful to think of A as a subobject of B with f being the embedding of A into B, and of C as the corresponding factor object B/A, with the map g being the natural projection from B to B/A (whose kernel is exactly A).
Facts
The splitting lemmaSplitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
states that if the above short exact sequence admits a morphism t: B → A such that t o f is the identity on A or
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
a morphism u: C → B such that g o u is the identity on C, then B is a twisted direct sum of A and C.
(For groups, a twisted direct sum is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
; in an abelian category, every twisted direct sum is an ordinary direct sum
Biproduct
In category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
.)
In this case, we say that the short exact sequence splits.
The snake lemma
Snake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
shows how a commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
with two exact rows gives rise to a longer exact sequence. The nine lemma
Nine lemma
In mathematics, the nine lemma is a statement about commutative diagrams and exact sequences valid in any abelian category, as well as in the category of groups. It states: ifis a commutative diagram and all columns as well as the two bottom rows are exact, then the top row is exact as well...
is a special case.
The five lemma
Five lemma
In mathematics, especially homological algebra and other applications of abelian category theory, the five lemma is an important and widely used lemma about commutative diagrams....
gives conditions under which the middle map in a commutative diagram with exact rows of length 5 is an isomorphism; the short five lemma
Short five lemma
In mathematics, especially homological algebra and other applications of abelian category theory, the short five lemma is a special case of the five lemma....
is a special case thereof applying to short exact sequences.
The importance of short exact sequences is underlined by the fact that every exact sequence results from "weaving together" several overlapping short exact sequences. Consider for instance the exact sequence
,which implies that there exist objects
in the category such that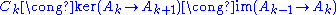.Suppose in addition that the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of each morphism exists, and is isomorphic to the image of the next morphism in the sequence:
(This is true for a number of interesting categories, including any abelian category such as the abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s; but it is not true for all categories that allow exact sequences, and in particular is not true for the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, in which
is not but 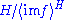, the quotient of H by the conjugate closureConjugate closure
In group theory, the conjugate closure of a subset S of a group G is the subgroup of G generated by SG, i.e. the closure of SG under the group operation, where SG is the conjugates of the elements of S:The conjugate closure of S is denoted or G.The conjugate closure of any subset S of a group G...
of
.) Then we obtain a commutative diagram in which all the diagonals are short exact sequences:
Note that the only portion of this diagram that depends on the cokernel condition is the object
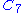and the final pair of morphisms 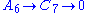. If there exists any object 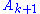and morphism 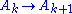such that is exact, then the exactness of 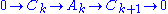is ensured. Again taking the example of the category of groups, the fact that is the kernel of some homomorphism on H implies that it is a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, which coincides with its conjugate closure; thus
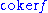is isomorphic to the image of the next morphism.Conversely, given any list of overlapping short exact sequences, their middle terms form an exact sequence in the same manner.
Applications of exact sequences
In the theory of abelian categories, short exact sequences are often used as a convenient language to talk about sub- and factor objects.The extension problem is essentially the question "Given the end terms A and C of a short exact sequence, what possibilities exist for the middle term B?" In the category of groups, this is equivalent to the question, what groups B have A as a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
and C as the corresponding factor group? This problem is important in the classification of groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. See also Outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
.
Notice that in an exact sequence, the composition fi+1 o fi maps Ai to 0 in Ai+2, so every exact sequence is a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
.
Furthermore, only fi-images of elements of Ai are mapped to 0 by fi+1, so the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of this chain complex is trivial. More succinctly:
- Exact sequences are precisely those chain complexes which are acyclicAcyclicAcyclic can refer to:* In chemistry, a compound which is not cyclic, e.g. alkanes and acyclic aliphatic compounds* In mathematics:** A graph without a cycle, especially*** A directed acyclic graph...
.
Given any chain complex, its homology can therefore be thought of as a measure of the degree to which it fails to be exact.
If we take a series of short exact sequences linked by chain complexes (that is, a short exact sequence of chain complexes, or from another point of view, a chain complex of short exact sequences), then we can derive from this a long exact sequence (i.e. an exact sequence indexed by the natural numbers) on homology by application of the zig-zag lemma
Zig-zag lemma
In mathematics, particularly homological algebra, the zig-zag lemma asserts the existence of a particular long exact sequence in the homology groups of certain chain complexes...
. It comes up in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
in the study of relative homology
Relative homology
In algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
; the Mayer–Vietoris sequence is another example. Long exact sequences induced by short exact sequences are also characteristic of derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s.
Exact functor
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
s are functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s that transform exact sequences into exact sequences.