
Gradient theorem
Encyclopedia
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral
through a gradient
field (any conservative vector field
can be expressed as the gradient of a scalar field
) can be evaluated by evaluating the original scalar field at the endpoints of the curve:
It is a generalization of the fundamental theorem of calculus
to any curve in a plane or space (generally n-dimensional) rather than just the real line.
The gradient theorem implies that line integrals through irrotational vector fields are path independent.
In physics this theorem is one of the ways of defining a "conservative" force
.
By placing as potential,
as potential, 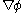 is a conservative field. Work done by conservative forces does not depend on the path followed by the object, but only the end points, as the above equation shows.
is a conservative field. Work done by conservative forces does not depend on the path followed by the object, but only the end points, as the above equation shows.
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
through a gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
field (any conservative vector field
Irrotational vector field
In vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
can be expressed as the gradient of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
) can be evaluated by evaluating the original scalar field at the endpoints of the curve:

It is a generalization of the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
to any curve in a plane or space (generally n-dimensional) rather than just the real line.
The gradient theorem implies that line integrals through irrotational vector fields are path independent.
In physics this theorem is one of the ways of defining a "conservative" force
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
.
By placing
 as potential,
as potential, 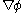 is a conservative field. Work done by conservative forces does not depend on the path followed by the object, but only the end points, as the above equation shows.
is a conservative field. Work done by conservative forces does not depend on the path followed by the object, but only the end points, as the above equation shows.

