
Complex differential form
Encyclopedia
In mathematics
, a complex differential form is a differential form
on a manifold
(usually a complex manifold
) which is permitted to have complex
coefficients.
Complex forms have broad applications in differential geometry. On complex manifolds, they are fundamental and serve as the basis for much of algebraic geometry
, Kähler geometry, and Hodge theory
. Over non-complex manifolds, they also play a role in the study of almost complex structures, the theory of spinor
s, and CR structures.
Typically, complex forms are considered because of some desirable decomposition that the forms admit. On a complex manifold, for instance, any complex k-form can be decomposed uniquely into a sum of so-called (p,q)-forms: roughly, wedges of p differentials
of the holomorphic coordinates with q differentials of their complex conjugates. The ensemble of (p,q)-forms becomes the primitive object of study, and determines a finer geometrical structure on the manifold than the k-forms. Even finer structures exist, for example, in cases where Hodge theory
applies.
. Then there is a local coordinate system
consisting of n complex-valued functions z1,...,zn such that the coordinate transitions from one patch to another are holomorphic function
s of these variables. The space of complex forms carries a rich structure, depending fundamentally on the fact that these transition functions are holomorphic, rather than just smooth.
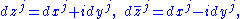
one sees that any differential form with complex coefficients can be written uniquely as a sum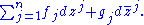
Let Ω1,0 be the space of complex differential forms containing only 's and Ω0,1 be the space of forms containing only
's and Ω0,1 be the space of forms containing only 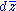 's. One can show, by the Cauchy-Riemann equations
's. One can show, by the Cauchy-Riemann equations
, that the spaces Ω1,0 and Ω0,1 are stable under holomorphic coordinate changes. In other words, if one makes a different choice wi of holomorphic coordinate system, then elements of Ω1,0 transform tensorially
, as do elements of Ω0,1. Thus the spaces Ω0,1 and Ω1,0 determine complex vector bundle
s on the complex manifold.
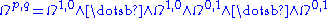
where there are p factors of Ω1,0 and q factors of Ω0,1. Just as with the two spaces of 1-forms, these are stable under holomorphic changes of coordinates, and so determine vector bundles.
If Ek is the space of all complex differential forms of total degree k, then each element of Ek can be expressed in a unique way as a linear combination of elements from among the spaces Ωp,q with p+q=k. More succinctly, there is a direct sum decomposition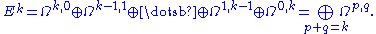
Because this direct sum decomposition is stable under holomorphic coordinate changes, it also determines a vector bundle decomposition.
In particular, for each k and each p and q with p+q=k, there is a canonical projection of vector bundles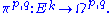
Using d and the projections defined in the previous subsection, it is possible to define the Dolbeault operators: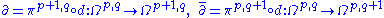
To describe these operators in local coordinates, let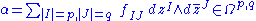
where I and J are multi-indices. Then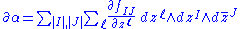
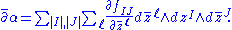
The following properties are seen to hold: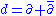

These operators and their properties form the basis for Dolbeault cohomology
and many aspects of Hodge theory
.

where the fI are holomorphic functions. Equivalently, the (p,0)-form α is holomorphic if and only if
The sheaf
of holomorphic p-forms is often written Ωp, although this can sometimes lead to confusion so many authors tend to adopt an alternative notation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a complex differential form is a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(usually a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
) which is permitted to have complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients.
Complex forms have broad applications in differential geometry. On complex manifolds, they are fundamental and serve as the basis for much of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Kähler geometry, and Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
. Over non-complex manifolds, they also play a role in the study of almost complex structures, the theory of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s, and CR structures.
Typically, complex forms are considered because of some desirable decomposition that the forms admit. On a complex manifold, for instance, any complex k-form can be decomposed uniquely into a sum of so-called (p,q)-forms: roughly, wedges of p differentials
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of the holomorphic coordinates with q differentials of their complex conjugates. The ensemble of (p,q)-forms becomes the primitive object of study, and determines a finer geometrical structure on the manifold than the k-forms. Even finer structures exist, for example, in cases where Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
applies.
Differential forms on a complex manifold
Suppose that M is a complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
. Then there is a local coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
consisting of n complex-valued functions z1,...,zn such that the coordinate transitions from one patch to another are holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of these variables. The space of complex forms carries a rich structure, depending fundamentally on the fact that these transition functions are holomorphic, rather than just smooth.
One-forms
We begin with the case of one-forms. First decompose the complex coordinates into their real and imaginary parts: zj=xj+iyj for each j. Letting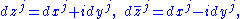
one sees that any differential form with complex coefficients can be written uniquely as a sum
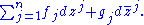
Let Ω1,0 be the space of complex differential forms containing only
 's and Ω0,1 be the space of forms containing only
's and Ω0,1 be the space of forms containing only 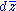 's. One can show, by the Cauchy-Riemann equations
's. One can show, by the Cauchy-Riemann equationsCauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
, that the spaces Ω1,0 and Ω0,1 are stable under holomorphic coordinate changes. In other words, if one makes a different choice wi of holomorphic coordinate system, then elements of Ω1,0 transform tensorially
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, as do elements of Ω0,1. Thus the spaces Ω0,1 and Ω1,0 determine complex vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s on the complex manifold.
Higher degree forms
The wedge product of complex differential forms is defined in the same way as with real forms. Let p and q be a pair of non-negative integers ≤ n. The space Ωp,q of (p,q)-forms is defined by taking linear combinations of the wedge products of p elements from Ω1,0 and q elements from Ω0,1. Symbolically,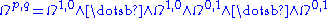
where there are p factors of Ω1,0 and q factors of Ω0,1. Just as with the two spaces of 1-forms, these are stable under holomorphic changes of coordinates, and so determine vector bundles.
If Ek is the space of all complex differential forms of total degree k, then each element of Ek can be expressed in a unique way as a linear combination of elements from among the spaces Ωp,q with p+q=k. More succinctly, there is a direct sum decomposition
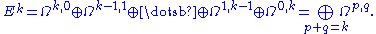
Because this direct sum decomposition is stable under holomorphic coordinate changes, it also determines a vector bundle decomposition.
In particular, for each k and each p and q with p+q=k, there is a canonical projection of vector bundles
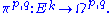
The Dolbeault operators
The usual exterior derivative defines a mapping of sections d:Ek→Ek+1. Restricting this to sections of Ωp,q, one can show that in fact d:Ωp,q→Ωp+1,q + Ωp,q+1. The exterior derivative does not in itself reflect the more rigid complex structure of the manifold.Using d and the projections defined in the previous subsection, it is possible to define the Dolbeault operators:
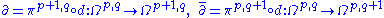
To describe these operators in local coordinates, let
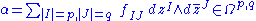
where I and J are multi-indices. Then
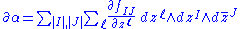
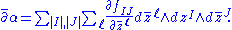
The following properties are seen to hold:
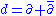

These operators and their properties form the basis for Dolbeault cohomology
Dolbeault cohomology
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold...
and many aspects of Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
.
Holomorphic forms
For each p, a holomorphic p-form is a holomorphic section of the bundle Ωp,0. In local coordinates, then, a holomorphic p-form can be written in the form
where the fI are holomorphic functions. Equivalently, the (p,0)-form α is holomorphic if and only if

The sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of holomorphic p-forms is often written Ωp, although this can sometimes lead to confusion so many authors tend to adopt an alternative notation.
See also
- Dolbeault complex
- Fröhlicher spectral sequenceFröhlicher spectral sequenceIn mathematics, the Fröhlicher spectral sequence is a tool in the theory of complex manifolds, for expressing the potential failure of the results of cohomology theory that are valid in general only for Kähler manifolds. A spectral sequence is set up, the degeneration of which would give the...
- Differential of the first kindDifferential of the first kindIn mathematics, differential of the first kind is a traditional term used in the theories of Riemann surfaces and algebraic curves , for everywhere-regular differential 1-forms...

