Tensor (intrinsic definition)
Encyclopedia
In mathematics
, the modern component-free approach to the theory of a tensor views a tensor as an abstract object
, expressing some definite type of multi-linear concept. Their well-known properties can be derived from their definitions, as linear maps or more generally; and the rules for manipulations of tensors arise as an extension of linear algebra
to multilinear algebra
.
In differential geometry an intrinsic geometric statement may be described by a tensor field
on a manifold
, and then doesn't need to make reference to coordinates at all. The same is true in general relativity
, of tensor fields describing a physical property
. The component-free approach is also used heavily in abstract algebra
and homological algebra
, where tensors arise naturally.
s over a common field
F, one may form their tensor product V1 ⊗ ... ⊗ Vn. An element of this tensor product is referred to as a tensor (but this is not the notion of tensor discussed in this article).
A tensor on the vector space V is then defined to be an element of (i.e., a vector in) a vector space of the form:
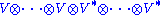
where V* is the dual space
of V.
If there are m copies of V and n copies of V* in our product, the tensor is said to be of type (m, n) and contravariant of order m and covariant order n and total order m+n. The tensors of order zero are just the scalars (elements of the field F), those of contravariant order 1 are the vectors in V, and those of covariant order 1 are the one-forms
in V* (for this reason the last two spaces are often called the contravariant and covariant vectors). The space of all tensors of type (m,n) is denoted
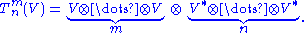
The (1,1) tensors
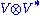
are isomorphic in a natural way to the space of linear transformations from V to V. An inner product
of a real vector space V; V × V → R corresponds in a natural way to a (0,2) tensor in
called the associated metric
and usually denoted g.
:
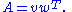
More generally, the rank of a matrix is the length of the smallest decomposition of a matrix A into a sum of such outer products: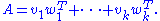
Similarly, a tensor of rank one (also called a simple tensor) is a tensor that can be written as a tensor product of the form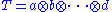
where a, b,...,d are in V or V*. That is, if the tensor is completely factorizable
. In indices, a tensor of rank 1 is a tensor of the form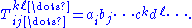
Every tensor can be expressed as a sum of rank 1 tensors. The rank of a general tensor T is defined to be the minimum number of rank 1 tensors with which it is possible to express T as a sum .
A tensor of order 1 always has rank 1 (or 0, in the case of the zero tensor). The rank of a tensor of order 2 agrees with the rank when the tensor is regarded as a matrix
, and can be determined from Gaussian elimination
for instance. The rank of an order 3 or higher tensor is however often very hard to determine, and low rank decompositions of tensors are sometimes of great practical interest . Computational tasks such as the efficient multiplication of matrices and the efficient evaluation of polynomials can be recast as the problem of simultaneously evaluating a set of bilinear forms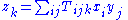
for given inputs xi and yj. If a low-rank decomposition of the tensor T is known, then an efficient evaluation strategy
is known .
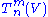can be characterized by a universal property
in terms of multilinear mappings. Amongst the advantages of this approach are that it gives a way to show that many linear mappings are "natural" or "geometric" (in other words are independent of any choice of basis). Explicit computational information can then be written down using bases, and this order of priorities can be more convenient than proving a formula gives rise to a natural mapping. Another aspect is that tensor products are not used only for free module
s, and the "universal" approach carries over more easily to more general situations.
A scalar-valued function on a Cartesian product
(or direct sum
) of vector spaces
is multilinear if it is linear in each argument. The space of all multlinear mappings from the product V1×V2×...×VN into W is denoted
LN(V1,V2,...,VN; W). When N = 1, a multilinear mapping is just an ordinary linear mapping, and the space of all linear mappings from V to W is denoted L(V;W).
The universal characterization of the tensor product implies that, for each multilinear function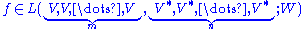
there exists a unique linear function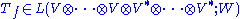
such that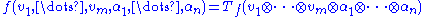
for all vi ∈ V and αi ∈ V∗.
Using the universal property, it follows that the space of (m,n)-tensors admits a natural isomorphism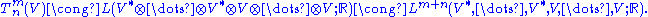
In the formula above, the roles of V and V* are reversed. In particular, one has
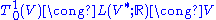
and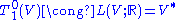
and
and engineering
must often deal with tensor field
s on smooth manifolds. The term tensor is in fact sometimes used as a shorthand for tensor field. A tensor field expresses the concept of a tensor that varies from point to point.
). The difference between the raised and lowered indices is there to remind us of the way the components transform.
For example purposes, then, take a tensor A in the space
The components relative to our coordinate system can be written
.
Here we used the Einstein notation
, a convention useful when dealing with coordinate equations: when an index variable appears both raised and lowered on the same side of an equation, we are summing over all its possible values. In physics we often use the expression
to represent the tensor, just as vectors
are usually treated in terms of their components. This can be visualized as an n × n × n array of numbers. In a different coordinate system, say given to us as a basis {ei'}, the components will be different. If (xi'i) is our transformation matrix (note it is not a tensor, since it represents a change of basis rather than a geometrical entity) and if (yii') is its inverse, then our components vary per
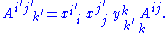
In older texts this transformation rule often serves as the definition of a tensor. Formally, this means that tensors were introduced as specific representations
of the group
of all changes of coordinate systems.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the modern component-free approach to the theory of a tensor views a tensor as an abstract object
Abstract object
An abstract object is an object which does not exist at any particular time or place, but rather exists as a type of thing . In philosophy, an important distinction is whether an object is considered abstract or concrete. Abstract objects are sometimes called abstracta An abstract object is an...
, expressing some definite type of multi-linear concept. Their well-known properties can be derived from their definitions, as linear maps or more generally; and the rules for manipulations of tensors arise as an extension of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
to multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
.
In differential geometry an intrinsic geometric statement may be described by a tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, and then doesn't need to make reference to coordinates at all. The same is true in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, of tensor fields describing a physical property
Physical property
A physical property is any property that is measurable whose value describes a physical system's state. The changes in the physical properties of a system can be used to describe its transformations ....
. The component-free approach is also used heavily in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, where tensors arise naturally.
- Note: This article assumes an understanding of the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s without chosen basesBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. An overview of the subject can be found in the main tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
article.
Definition via tensor products of vector spaces
Given a finite set { V1, ... , Vn } of vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a common field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, one may form their tensor product V1 ⊗ ... ⊗ Vn. An element of this tensor product is referred to as a tensor (but this is not the notion of tensor discussed in this article).
A tensor on the vector space V is then defined to be an element of (i.e., a vector in) a vector space of the form:
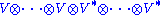
where V* is the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of V.
If there are m copies of V and n copies of V* in our product, the tensor is said to be of type (m, n) and contravariant of order m and covariant order n and total order m+n. The tensors of order zero are just the scalars (elements of the field F), those of contravariant order 1 are the vectors in V, and those of covariant order 1 are the one-forms
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
in V* (for this reason the last two spaces are often called the contravariant and covariant vectors). The space of all tensors of type (m,n) is denoted
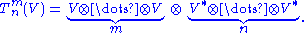
The (1,1) tensors
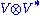
are isomorphic in a natural way to the space of linear transformations from V to V. An inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
of a real vector space V; V × V → R corresponds in a natural way to a (0,2) tensor in
called the associated metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
and usually denoted g.
Tensor rank
The term rank of a tensor is often used interchangeably with the order (or degree) of a tensor. However, it is also used in a different unrelated sense that extends the notion of the rank of a matrix given in linear algebra. The rank of a matrix is the minimum number of column vectors needed to span the range of the matrix. A matrix thus has rank one if it can be written as an outer productOuter product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
:
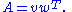
More generally, the rank of a matrix is the length of the smallest decomposition of a matrix A into a sum of such outer products:
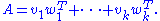
Similarly, a tensor of rank one (also called a simple tensor) is a tensor that can be written as a tensor product of the form
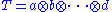
where a, b,...,d are in V or V*. That is, if the tensor is completely factorizable
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
. In indices, a tensor of rank 1 is a tensor of the form
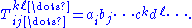
Every tensor can be expressed as a sum of rank 1 tensors. The rank of a general tensor T is defined to be the minimum number of rank 1 tensors with which it is possible to express T as a sum .
A tensor of order 1 always has rank 1 (or 0, in the case of the zero tensor). The rank of a tensor of order 2 agrees with the rank when the tensor is regarded as a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, and can be determined from Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
for instance. The rank of an order 3 or higher tensor is however often very hard to determine, and low rank decompositions of tensors are sometimes of great practical interest . Computational tasks such as the efficient multiplication of matrices and the efficient evaluation of polynomials can be recast as the problem of simultaneously evaluating a set of bilinear forms
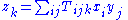
for given inputs xi and yj. If a low-rank decomposition of the tensor T is known, then an efficient evaluation strategy
Evaluation strategy
In computer science, an evaluation strategy is a set of rules for evaluating expressions in a programming language. Emphasis is typically placed on functions or operators: an evaluation strategy defines when and in what order the arguments to a function are evaluated, when they are substituted...
is known .
Universal property
The space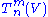 can be characterized by a universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in terms of multilinear mappings. Amongst the advantages of this approach are that it gives a way to show that many linear mappings are "natural" or "geometric" (in other words are independent of any choice of basis). Explicit computational information can then be written down using bases, and this order of priorities can be more convenient than proving a formula gives rise to a natural mapping. Another aspect is that tensor products are not used only for free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s, and the "universal" approach carries over more easily to more general situations.
A scalar-valued function on a Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
(or direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
) of vector spaces
is multilinear if it is linear in each argument. The space of all multlinear mappings from the product V1×V2×...×VN into W is denoted
LN(V1,V2,...,VN; W). When N = 1, a multilinear mapping is just an ordinary linear mapping, and the space of all linear mappings from V to W is denoted L(V;W).
The universal characterization of the tensor product implies that, for each multilinear function
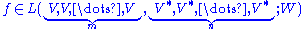
there exists a unique linear function
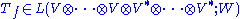
such that
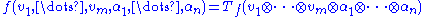
for all vi ∈ V and αi ∈ V∗.
Using the universal property, it follows that the space of (m,n)-tensors admits a natural isomorphism
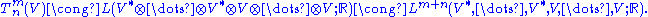
In the formula above, the roles of V and V* are reversed. In particular, one has
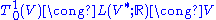
and
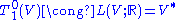
and
Tensor fields
Differential geometry, physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
must often deal with tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s on smooth manifolds. The term tensor is in fact sometimes used as a shorthand for tensor field. A tensor field expresses the concept of a tensor that varies from point to point.
Basis
For any given coordinate system we have a basis {ei} for the tangent space V (this may vary from point-to-point if the manifold is not linear), and a corresponding dual basis {ei} for the cotangent space V* (see dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
). The difference between the raised and lowered indices is there to remind us of the way the components transform.
For example purposes, then, take a tensor A in the space
The components relative to our coordinate system can be written
.Here we used the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, a convention useful when dealing with coordinate equations: when an index variable appears both raised and lowered on the same side of an equation, we are summing over all its possible values. In physics we often use the expression
to represent the tensor, just as vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
are usually treated in terms of their components. This can be visualized as an n × n × n array of numbers. In a different coordinate system, say given to us as a basis {ei'}, the components will be different. If (xi'i) is our transformation matrix (note it is not a tensor, since it represents a change of basis rather than a geometrical entity) and if (yii') is its inverse, then our components vary per
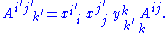
In older texts this transformation rule often serves as the definition of a tensor. Formally, this means that tensors were introduced as specific representations
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all changes of coordinate systems.