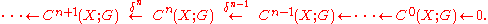Cohomology
Encyclopedia
In mathematics
, specifically in algebraic topology
, cohomology is a general term for a sequence
of abelian group
s defined from a co-chain complex
. That is, cohomology is defined as the abstract study of cochains, cocycle
s, and coboundaries. Cohomology can be viewed as a method of assigning algebraic invariants to a topological space that has a more refined algebraic structure
than does homology
. Cohomology arises from the algebraic dualization of the construction of homology. In less abstract language, cochains in the fundamental sense should assign 'quantities' to the chains
of homology theory.
From its beginning in topology
, this idea became a dominant method in the mathematics of the second half of the twentieth century; from the initial idea of homology as a topologically invariant relation on chains, the range of applications of homology and cohomology theories has spread out over geometry
and abstract algebra
. The terminology tends to mask the fact that in many applications cohomology, a contravariant theory, is more natural than homology. At a basic level this has to do with function
s and pullbacks in geometric situations: given spaces X and Y, and some kind of function F on Y, for any mapping
ƒ: X → Y composition with ƒ gives rise to a function F o ƒ on X.
Cohomology groups often also have a natural product, the cup product
, which gives them a ring
structure. Because of this feature, cohomology is a stronger invariant than homology, as it can differentiate between certain algebraic objects that homology cannot.
Elements in Ker(δn) are n-cocycles and elements in Im(δn-1) are n-coboundaries. The cohomology groups with n ≥ 1 are called the higher cohomology.
, its importance was not seen for some 40 years after the development of homology. The concept of dual cell structure, which Henri Poincaré
used in his proof of his Poincaré duality
theorem, contained the germ of the idea of cohomology, but this was not seen until later.
There were various precursors to cohomology. In the mid-1920s, J.W. Alexander and Solomon Lefschetz
founded the intersection theory
of cycles on manifold
s. On an n-dimension
al manifold M, a p-cycle and a q-cycle with nonempty intersection will, if in general position
, have intersection a (p + q − n)-cycle. This enables us to define a multiplication of homology classes
Alexander
had by 1930 defined a first cochain notion, based on a p-cochain on a space X having relevance to the small neighborhoods of the diagonal
in Xp+1.
In 1931, Georges de Rham
related homology and exterior differential form
s, proving De Rham's theorem. This result is now understood to be more naturally interpreted in terms of cohomology.
In 1934, Lev Pontryagin proved the Pontryagin duality
theorem; a result on topological group
s. This (in rather special cases) provided an interpretation of Poincaré duality
and Alexander duality
in terms of group
character
s.
At a 1935 conference in Moscow
, Andrey Kolmogorov
and Alexander
both introduced cohomology and tried to construct a cohomology product structure.
In 1936 Norman Steenrod
published a paper constructing Čech cohomology
by dualizing Čech homology.
From 1936 to 1938, Hassler Whitney
and Eduard Čech
developed the cup product
(making cohomology into a graded ring) and cap product
, and realized that Poincaré duality can be stated in terms of the cap product. Their theory was still limited to finite cell complexes.
In 1944, Samuel Eilenberg
overcame the technical limitations, and gave the modern definition of singular homology
and cohomology.
In 1945, Eilenberg and Steenrod stated the axioms defining a homology or cohomology theory. In their 1952 book, Foundations of Algebraic Topology, they proved that the existing homology and cohomology theories did indeed satisfy their axioms.
In 1948 Edwin Spanier
, building on work of Alexander and Kolmogorov, developed Alexander–Spanier cohomology.
s from the category
of pairs of topological space
s and continuous function
s (or some subcategory
thereof such as the category of CW complex
es) to the category of Abelian group
s and group homomorphism
s that satisfies the Eilenberg–Steenrod axioms.
Some cohomology theories in this sense are:
and cobordism theory. There are others, coming from stable homotopy theory
. In this context, singular homology
is referred to as ordinary homology.
A generalized cohomology theory is "determined by its values on a point", in the sense that if one has a space given by contractible spaces (homotopy equivalent to a point), glued together along contractible spaces, as in a simplicial complex
, then the cohomology of the space is determined by the cohomology of a point and the combinatorics of the patching, and effectively computable.
Formally, this is computed by the excision theorem
, or equivalently the Mayer–Vietoris sequence. Thus the cohomology of a point is a fundamental calculation for any generalized cohomology theory, though the cohomology of particular spaces is also of interest.
One reason that generalized cohomology theories are interesting is that they are representable functors
if one works in a larger category
than CW complexes
; namely, the category of spectra
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, cohomology is a general term for a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s defined from a co-chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
. That is, cohomology is defined as the abstract study of cochains, cocycle
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
s, and coboundaries. Cohomology can be viewed as a method of assigning algebraic invariants to a topological space that has a more refined algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
than does homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
. Cohomology arises from the algebraic dualization of the construction of homology. In less abstract language, cochains in the fundamental sense should assign 'quantities' to the chains
Chain (algebraic topology)
In algebraic topology, a simplicial k-chainis a formal linear combination of k-simplices.-Integration on chains:Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients typically integers.The set of all k-chains forms a group...
of homology theory.
From its beginning in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, this idea became a dominant method in the mathematics of the second half of the twentieth century; from the initial idea of homology as a topologically invariant relation on chains, the range of applications of homology and cohomology theories has spread out over geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. The terminology tends to mask the fact that in many applications cohomology, a contravariant theory, is more natural than homology. At a basic level this has to do with function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s and pullbacks in geometric situations: given spaces X and Y, and some kind of function F on Y, for any mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
ƒ: X → Y composition with ƒ gives rise to a function F o ƒ on X.
Cohomology groups often also have a natural product, the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
, which gives them a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
structure. Because of this feature, cohomology is a stronger invariant than homology, as it can differentiate between certain algebraic objects that homology cannot.
Definition
For a topological space X, the cohomology group Hn(X;G), with coefficents in G, is defined to be the quotient Ker(δn)/Im(δn-1) at Cn(X;G) in the cochain complexElements in Ker(δn) are n-cocycles and elements in Im(δn-1) are n-coboundaries. The cohomology groups with n ≥ 1 are called the higher cohomology.
History
Although cohomology is fundamental to modern algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, its importance was not seen for some 40 years after the development of homology. The concept of dual cell structure, which Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
used in his proof of his Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
theorem, contained the germ of the idea of cohomology, but this was not seen until later.
There were various precursors to cohomology. In the mid-1920s, J.W. Alexander and Solomon Lefschetz
Solomon Lefschetz
Solomon Lefschetz was an American mathematician who did fundamental work on algebraic topology, its applications to algebraic geometry, and the theory of non-linear ordinary differential equations.-Life:...
founded the intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
of cycles on manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. On an n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al manifold M, a p-cycle and a q-cycle with nonempty intersection will, if in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
, have intersection a (p + q − n)-cycle. This enables us to define a multiplication of homology classes
- Hp(M) × Hq(M) → Hp+q−n(M).
Alexander
James Waddell Alexander II
James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...
had by 1930 defined a first cochain notion, based on a p-cochain on a space X having relevance to the small neighborhoods of the diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
in Xp+1.
In 1931, Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
related homology and exterior differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s, proving De Rham's theorem. This result is now understood to be more naturally interpreted in terms of cohomology.
In 1934, Lev Pontryagin proved the Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
theorem; a result on topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s. This (in rather special cases) provided an interpretation of Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
and Alexander duality
Alexander duality
In mathematics, Alexander duality refers to a duality theory presaged by a result of 1915 by J. W. Alexander, and subsequently further developed, particularly by P. S. Alexandrov and Lev Pontryagin...
in terms of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
s.
At a 1935 conference in Moscow
Moscow
Moscow is the capital, the most populous city, and the most populous federal subject of Russia. The city is a major political, economic, cultural, scientific, religious, financial, educational, and transportation centre of Russia and the continent...
, Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
and Alexander
James Waddell Alexander II
James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...
both introduced cohomology and tried to construct a cohomology product structure.
In 1936 Norman Steenrod
Norman Steenrod
Norman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
published a paper constructing Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
by dualizing Čech homology.
From 1936 to 1938, Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
and Eduard Čech
Eduard Cech
Eduard Čech was a Czech mathematician born in Stračov, Bohemia . His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin...
developed the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
(making cohomology into a graded ring) and cap product
Cap product
In algebraic topology the cap product is a method of adjoining a chain of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech in 1936, and independently by Hassler Whitney in 1938.-Definition:Let X be a topological...
, and realized that Poincaré duality can be stated in terms of the cap product. Their theory was still limited to finite cell complexes.
In 1944, Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
overcame the technical limitations, and gave the modern definition of singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and cohomology.
In 1945, Eilenberg and Steenrod stated the axioms defining a homology or cohomology theory. In their 1952 book, Foundations of Algebraic Topology, they proved that the existing homology and cohomology theories did indeed satisfy their axioms.
In 1948 Edwin Spanier
Edwin Spanier
Edwin Henry Spanier was an American mathematician at the University of California at Berkeley, working in algebraic topology...
, building on work of Alexander and Kolmogorov, developed Alexander–Spanier cohomology.
Eilenberg–Steenrod theories
A cohomology theory is a family of contravariant functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s from the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of pairs of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s (or some subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
thereof such as the category of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es) to the category of Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and group homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s that satisfies the Eilenberg–Steenrod axioms.
Some cohomology theories in this sense are:
- simplicial cohomology
- singular cohomology
- de Rham cohomologyDe Rham cohomologyIn mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
- Čech cohomologyCech cohomologyIn mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
- sheaf cohomologySheaf cohomologyIn mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
.
Generalized cohomology theories
When one axiom (the dimension axiom) is relaxed, one obtains the idea of generalized cohomology theory or extraordinary cohomology theory; this allows theories based on K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
and cobordism theory. There are others, coming from stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
. In this context, singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
is referred to as ordinary homology.
A generalized cohomology theory is "determined by its values on a point", in the sense that if one has a space given by contractible spaces (homotopy equivalent to a point), glued together along contractible spaces, as in a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
, then the cohomology of the space is determined by the cohomology of a point and the combinatorics of the patching, and effectively computable.
Formally, this is computed by the excision theorem
Excision theorem
In algebraic topology, a branch of mathematics, the excision theorem is a useful theorem about relative homology—given topological spaces X and subspaces A and U such that U is also a subspace of A, the theorem says that under certain circumstances, we can cut out U from both spaces such...
, or equivalently the Mayer–Vietoris sequence. Thus the cohomology of a point is a fundamental calculation for any generalized cohomology theory, though the cohomology of particular spaces is also of interest.
One reason that generalized cohomology theories are interesting is that they are representable functors
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
if one works in a larger category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
than CW complexes
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
; namely, the category of spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
.
Other cohomology theories
Theories in a broader sense of cohomology include:- André–Quillen cohomologyAndré–Quillen cohomologyIn commutative algebra, André–Quillen cohomology is a theory of cohomology for commutative rings which is closely related to the cotangent complex. It was defined independently by M. André and by Daniel Quillen using methods of homotopy theory...
- BRST cohomology
- Bonar–Claven cohomology
- Bounded cohomology
- Coherent cohomology
- Crystalline cohomologyCrystalline cohomologyIn mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
- Cyclic cohomology
- Deligne cohomologyDeligne cohomologyIn mathematics, Deligne cohomology is the hypercohomology of the Deligne complex of a complex manifold. It was introduced by Pierre Deligne in unpublished work in about 1972 as a cohomology theory for algebraic varieties that includes both ordinary cohomology and intermediate Jacobians.For...
- Dirac cohomology
- Étale cohomologyÉtale cohomologyIn mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
- Flat cohomology
- Galois cohomologyGalois cohomologyIn mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
- Gel'fand–Fuks cohomology
- Group cohomologyGroup cohomologyIn abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
- Harrison cohomology
- Hochschild cohomology
- Intersection cohomologyIntersection cohomologyIn topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
- Lie algebra cohomologyLie algebra cohomologyIn mathematics, Lie algebra cohomology is a cohomology theory for Lie algebras. It was defined by in order to give an algebraic construction of the cohomology of the underlying topological spaces of compact Lie groups...
- Local cohomologyLocal cohomologyIn mathematics, local cohomology is a chapter of homological algebra and sheaf theory introduced into algebraic geometry by Alexander Grothendieck. He developed it in seminars in 1961 at Harvard University, and 1961-2 at IHES. It was later written up as SGA2...
- Motivic cohomologyMotivic cohomologyMotivic cohomology is a cohomological theory in mathematics, the existence of which was first conjectured by Alexander Grothendieck during the 1960s. At that time, it was conceived as a theory constructed on the basis of the so-called standard conjectures on algebraic cycles, in algebraic geometry...
- Non-abelian cohomology
- Perverse cohomology
- Quantum cohomologyQuantum cohomologyIn mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
- Schur cohomology
- Spencer cohomologySpencer cohomologyIn mathematics, Spencer cohomology is cohomology of a manifold with coefficients in the sheaf of solutions of a linear partial differential operator. It was introduced by ....
- Topological André–Quillen cohomology
- Topological cyclic cohomology
- Topological Hochschild cohomology
- Γ cohomology