In the mathematical field of
topologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a
section (or
cross section) of a
fiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
π is a continuous right inverse of the function π. In other words, if
π is a fiber bundle over a
base spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
,
B:
- π: E → B,
then a section of that fiber bundle is a continuous map,
- s : B → E,
such that
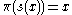for all
x in
B.
A section is a certain generalization of the notion of the
graph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
. The graph of a function
g :
B →
Y can be identified with a function taking its values in the
Cartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
E =
B×
Y of
B and
Y:
A section is an abstract characterization of what it means to be a graph. Let π :
E →
X be the projection onto the first factor: π(
x,
y) =
x. Then a graph is any function
s for which π(
s(
x))=
x.
The language of fibre bundles allows this notion of a section to be generalized to the case when
E is not necessarily a Cartesian product. If π :
E →
B is a fibre bundle, then a section is a choice of point
s(
x) in each of the fibres. The condition π(
s(
x)) =
x simply means that the section at a point
x must lie over
x. (See image.)
For example, when
E is a
vector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
a section of
E is an element of the vector space
Ex lying over each point
x ∈
B. In particular, a
vector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on a smooth manifold
M is a choice of
tangent vectorA tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
at each point of
M: this is a
section of the
tangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of
M. Likewise, a 1-form on
M is a section of the
cotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
.
Fiber bundles do not in general have such
global sections, so it is also useful to define sections only locally. A
local section of a fiber bundle is a continuous map
s :
U →
E where
U is an
open setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in
B and
π(
s(
x))=
x for all
x in
U. If (
U,
φ) is a local trivialization of
E, where
φ is a homeomorphism from
π-1(
U) to
U ×
F (where
F is the
fiberIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
), then local sections always exist over
U in bijective correspondence with continuous maps from
U to
F. The (local) sections form a
sheafIn mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
over
B called the
sheaf of sections of
E.
The space of continuous sections of a fiber bundle
E over
U is sometimes denoted
C(
U,
E), while the space of global sections of
E is often denoted Γ(
E) or Γ(
B,
E).
Sections are studied in homotopy theory and
algebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, where one of the main goals is to account for the existence or non-existence of
global sections. This leads to
sheaf cohomologyIn mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
and the theory of
characteristic classIn mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es. For example, a
principal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
has a global section if and only if it is trivial. On the other hand, a
vector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
always has a global section, namely the zero section. However, it only admits a nowhere vanishing section if its
Euler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is zero.
Sections, particularly of principal bundles and vector bundles, are also very important tools in differential geometry. In this setting, the base space
B is a smooth manifold
M, and
E is assumed to be a smooth fiber bundle over
M (i.e.,
E is a smooth manifold and
π:
E →
M is a smooth map). In this case, one considers the space of smooth sections of
E over an open set
U, denoted
C∞(
U,
E). It is also useful in
geometric analysisGeometric analysis is a mathematical discipline at the interface of differential geometry and differential equations. It includes both the use of geometrical methods in the study of partial differential equations , and the application of the theory of partial differential equations to geometry...
to consider spaces of sections with intermediate regularity (e.g.
Ck sections, or sections with regularity in the sense of
Hölder conditionIn mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
s or Sobolev spaces).
See also
- Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
- Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
- Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
- Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
- Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
External links