Ricci curvature
Encyclopedia
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro
, represents the amount by which the volume element
of a geodesic
ball
in a curved Riemannian manifold
deviates from that of the standard ball in Euclidean space
. As such, it provides one way of measuring the degree to which the geometry determined by a given Riemannian metric might differ from that of ordinary Euclidean n-space. The Ricci tensor is defined on any pseudo-Riemannian manifold
, as a trace of the Riemann curvature tensor
. Like the metric itself, the Ricci tensor is a symmetric bilinear form
on the tangent space
of the manifold .
In relativity theory, the Ricci tensor is the part of the curvature of space-time that determines the degree to which matter will tend to converge or diverge in time (via the Raychaudhuri equation
). It is related to the matter content of the universe by means of the Einstein field equation. In differential geometry, lower bounds on the Ricci tensor on a Riemannian manifold allow one to extract global geometric and topological information by comparison (cf. comparison theorem
) with the geometry of a constant curvature space form
. If the Ricci tensor satisfies the vacuum Einstein equation, then the manifold is an Einstein manifold
, which have been extensively studied (cf. ). In this connection, the Ricci flow
equation governs the evolution of a given metric to an Einstein metric, the precise manner in which this occurs ultimately leads to the solution of the Poincaré conjecture.
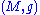is an n-dimensional Riemannian manifold
, equipped with its Levi-Civita connection
. The Riemannian curvature tensor of 
is the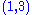 
tensor defined by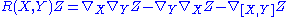
on vector field
s
. Let 
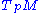denote the tangent space
of M at a point p. For any pair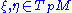
of tangent vectors at p, the Ricci tensor 
evaluated at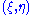 
is defined to be the trace
of the linear map
given by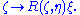
In local coordinates
(using the Einstein summation convention), one has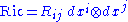
where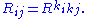
In terms of the Riemann curvature tensor
and the Christoffel symbols
, one has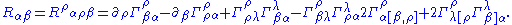
of a Riemannian manifold is symmetric, in the sense that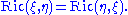
It thus follows that the Ricci tensor is completely determined by knowing the quantity
for all vectors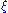
of unit length. This function on the set of unit tangent vectors is often simply called
the Ricci curvature, since knowing it is equivalent to knowing the Ricci curvature tensor.
The Ricci curvature is determined by the sectional curvature
s of a Riemannian manifold, but generally contains less information. Indeed, if
is a vector of unit length on a Riemannian n-manifold, then Ric(ξ,ξ) is precisely (n−1) times the average value of the sectional curvature, taken over all the 2-planes containing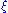 
. There is an (n−2)-dimensional family of such 2-planes, and so only in dimensions 2 and 3 does the Ricci tensor determine the full curvature tensor. A notable exception is when the manifold is given a priori as a hypersurface
of Euclidean space. The second fundamental form, which determines the full curvature via the Gauss-Codazzi equation, is itself determined by the Ricci tensor and the principal directions of the hypersurface are also the eigendirections of the Ricci tensor. The tensor was introduced by Ricci for this reason.
If the Ricci curvature function Ric(ξ,ξ) is constant on the set of unit tangent vectors ξ, the Riemannian manifold is said to have constant Ricci curvature, or to be an Einstein manifold
. This happens if and only if the Ricci tensor Ric is a constant multiple of the metric tensor g.
The Ricci curvature is usefully thought of as a multiple of the Laplacian of the metric tensor . Specifically, if xi are harmonic
local coordinates, then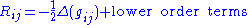
where Δ is the Laplace-Beltrami operator
regarded here as acting on the functions gij. This fact motivates, for instance, the introduction of the Ricci flow
equation as a natural extension of the heat equation
for the metric. Alternatively, in a normal coordinate system
based at p, at the point p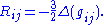
can define preferred local
coordinates, called geodesic normal coordinates. These are adapted
to the metric such that geodesics through p corresponds to straight lines through the origin,
in such a manner that the geodesic distance from p corresponds to the Euclidean distance from the origin.
In these coordinates, the metric tensor is well-approximated by the Euclidean metric, in the precise sense that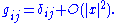
In fact, by taking the Taylor expansion of the metric applied to a Jacobi field
along a radial geodesic in the normal coordinate system, one has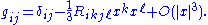
In these coordinates, the metric volume element
then has the following expansion at p:
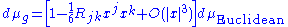
which follows by expanding the square root of the determinant
of the metric.
Thus, if the Ricci curvature Ric(ξ,ξ) is positive in the direction of a vector ξ,
the conical region in M swept out by a tightly focused family of
short geodesic segments emanating from p with initial velocity inside a small cone around ξ
will have smaller volume than the corresponding conical region in Euclidean space, just as the surface a small spherical wedge
has lesser area than a corresponding circular sector. Similarly, if the Ricci curvature is negative in the direction of a given vector ξ, such a conical region in the manifold will instead have larger volume than it would in Euclidean space.
The Ricci curvature is essentially an average of curvatures in the planes including ξ. Thus if a cone emitted with an initially circular (or spherical) cross-section becomes distorted into an ellipse (ellipsoid), it is possible for the volume distortion to vanish if the distortions along the principal axes counteract one another. The Ricci curvature would then vanish along ξ. In physical applications, the presence of a nonvanishing sectional curvature does not necessarily indicate the presence of any mass locally; if an initially circular cross-section of a cone of world-lines later becomes elliptical, without changing its volume, then this is due to tidal effects from a mass at some other location.
, where it is the key term in the Einstein field equations.
Ricci curvature also appears in the Ricci flow
equation, where a time-dependent Riemannian
metric is deformed in the direction of minus its Ricci curvature. This system of partial differential equations is a non-linear analog of the heat equation
, and was first
introduced by Richard Hamilton
in the early 1980s. Since heat tends to spread through a solid until the body reaches an equilibrium state of constant temperature, Ricci flow may be hoped to produce an equilibrium geometry for a manifold for which the Ricci curvature is constant. Recent contributions to the subject due to Grigori Perelman
now show that this program works well enough in dimension three to lead to a complete classification of compact 3-manifolds, along lines
first conjectured by William Thurston
in the 1970s.
On a Kähler manifold
, the Ricci curvature determines the first Chern class
of the manifold (mod torsion). However, the Ricci curvature has no analogous topological interpretation
on a generic Riemannian manifold.
These results show that positive Ricci curvature has strong topological consequences. By contrast, excluding the case of surfaces, negative
Ricci curvature is now known to have no topological implications; has shown that any manifold of dimension greater than two admits a Riemannian metric of negative Ricci curvature. (For surfaces, negative Ricci curvature implies negative sectional curvature; but the point
is that this fails rather dramatically in all higher dimensions.)
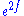, the Ricci tensor of the new, conformally related metric 
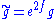is given by
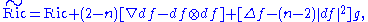
where Δ = d∗d is the (positive spectrum) Hodge Laplacian, i.e., the opposite of the usual trace of the Hessian.
In particular, given a point p in a Riemannian manifold, it is always possible to find metrics conformal to the given metric g for which the Ricci tensor vanishes at p. Note, however, that this is only pointwise assertion; it is usually impossible to make the Ricci curvature vanish identically on the entire manifold by a conformal rescaling.
For two dimensional manifolds, the above formula shows that if f is a harmonic function
, then the conformal scaling g e2ƒg does not change the Ricci curvature.
and general relativity
, the trace-free Ricci tensor of a pseudo-Riemannian
manifold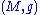
is the tensor defined by
where
is the Ricci tensor,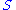 
is the scalar curvature
,
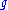is the metric tensor
, and
is the dimension of 
.
The name of this object reflects the fact that its trace
automatically vanishes:
If n
3, the trace-free Ricci tensor vanishes identically if and only if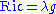
for some constant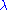
.
In mathematics, this is the condition for
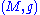to be an Einstein manifold
. In physics, this equation
states that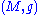
is a solution of Einstein's vacuum field
equations with cosmological constant
.
X, the Ricci curvature determines the curvature form
of the canonical line bundle
. The canonical line bundle is the top exterior power of the bundle of holomorphic Kähler differential
s: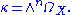
The Levi-Civita connection corresponding to the metric on X gives rise to a connection on κ. The curvature of this connection is the two form defined by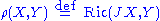
where J is the complex structure map of the Kähler manifold. The Ricci form is a closed two-form. Its cohomology class is, up to a real constant factor, the first Chern class
of the canonical bundle, and is therefore a topological invariant of X (for X compact) in the sense that it depends only on the topology of X and the homotopy class of the complex structure.
Conversely, the Ricci form determines the Ricci tensor by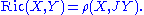
In local holomorphic coordinates zα, the Ricci form is given by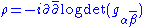
where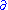
is the Dolbeault operator and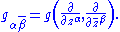
If the Ricci tensor vanishes, then the canonical bundle is flat, so the structure group
can be locally reduced to a subgroup of the special linear group SL(n,C). However, Kähler manifolds already possess holonomy
in U(n), and so the (restricted) holonomy of a Ricci flat Kähler manifold is contained in SU(n). Conversely, if the (restricted) holonomy of a 2n-dimensional Riemannian manifold is contained in SU(n), then the manifold is a Ricci-flat Kähler manifold .
s, where it is an invariant that plays an especially important role in the study of the projective geometry
(geometry associated to unparameterized geodesics) . If
denotes an affine connection, then the curvature tensor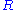 
is the 
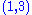tensor defined by
for any vector fields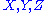
. The Ricci tensor is defined to be the trace:
In this more general situation, the Ricci tensor is symmetric if and only if there exists a parallel volume form
for the connection.
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
, represents the amount by which the volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
of a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
in a curved Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
deviates from that of the standard ball in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. As such, it provides one way of measuring the degree to which the geometry determined by a given Riemannian metric might differ from that of ordinary Euclidean n-space. The Ricci tensor is defined on any pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, as a trace of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. Like the metric itself, the Ricci tensor is a symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
on the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of the manifold .
In relativity theory, the Ricci tensor is the part of the curvature of space-time that determines the degree to which matter will tend to converge or diverge in time (via the Raychaudhuri equation
Raychaudhuri equation
In general relativity, the Raychaudhuri equation, or Landau-Raychaudhuri equation, is a fundamental result describing the motion of nearby bits of matter....
). It is related to the matter content of the universe by means of the Einstein field equation. In differential geometry, lower bounds on the Ricci tensor on a Riemannian manifold allow one to extract global geometric and topological information by comparison (cf. comparison theorem
Comparison theorem
A comparison theorem is any of a variety of theorems that compare properties of various mathematical objects.-Riemannian geometry:In Riemannian geometry it is a traditional name for a number of theorems that compare various metrics and provide various estimates in Riemannian geometry.*Rauch...
) with the geometry of a constant curvature space form
Space form
In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
. If the Ricci tensor satisfies the vacuum Einstein equation, then the manifold is an Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
, which have been extensively studied (cf. ). In this connection, the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
equation governs the evolution of a given metric to an Einstein metric, the precise manner in which this occurs ultimately leads to the solution of the Poincaré conjecture.
Definition
Suppose that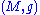 is an n-dimensional Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, equipped with its Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
. The Riemannian curvature tensor of is the 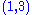tensor defined by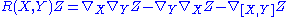on vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s
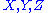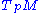. Let denote the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of M at a point p. For any pair
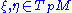of tangent vectors at p, the Ricci tensor evaluated at 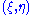is defined to be the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the linear map
given by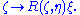In local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
(using the Einstein summation convention), one has
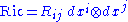
where
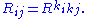
In terms of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
and the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
, one has
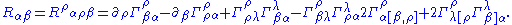
Properties
As a consequence of the Bianchi identities, the Ricci tensorof a Riemannian manifold is symmetric, in the sense that
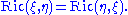
It thus follows that the Ricci tensor is completely determined by knowing the quantity
for all vectors
of unit length. This function on the set of unit tangent vectors is often simply calledthe Ricci curvature, since knowing it is equivalent to knowing the Ricci curvature tensor.
The Ricci curvature is determined by the sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
s of a Riemannian manifold, but generally contains less information. Indeed, if
is a vector of unit length on a Riemannian n-manifold, then Ric(ξ,ξ) is precisely (n−1) times the average value of the sectional curvature, taken over all the 2-planes containing . There is an (n−2)-dimensional family of such 2-planes, and so only in dimensions 2 and 3 does the Ricci tensor determine the full curvature tensor. A notable exception is when the manifold is given a priori as a hypersurfaceHypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
of Euclidean space. The second fundamental form, which determines the full curvature via the Gauss-Codazzi equation, is itself determined by the Ricci tensor and the principal directions of the hypersurface are also the eigendirections of the Ricci tensor. The tensor was introduced by Ricci for this reason.
If the Ricci curvature function Ric(ξ,ξ) is constant on the set of unit tangent vectors ξ, the Riemannian manifold is said to have constant Ricci curvature, or to be an Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
. This happens if and only if the Ricci tensor Ric is a constant multiple of the metric tensor g.
The Ricci curvature is usefully thought of as a multiple of the Laplacian of the metric tensor . Specifically, if xi are harmonic
Harmonic coordinates
In Riemannian geometry, a branch of mathematics, harmonic coordinates are a coordinate system on a Riemannian manifold each of whose coordinate functions xi is harmonic, meaning that it satisfies Laplace's equation\Delta x^i = 0.\,...
local coordinates, then
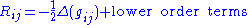
where Δ is the Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
regarded here as acting on the functions gij. This fact motivates, for instance, the introduction of the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
equation as a natural extension of the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
for the metric. Alternatively, in a normal coordinate system
Normal coordinates
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p...
based at p, at the point p
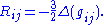
Direct geometric meaning
Near any point p in a Riemannian manifold (M,g), onecan define preferred local
coordinates, called geodesic normal coordinates. These are adapted
to the metric such that geodesics through p corresponds to straight lines through the origin,
in such a manner that the geodesic distance from p corresponds to the Euclidean distance from the origin.
In these coordinates, the metric tensor is well-approximated by the Euclidean metric, in the precise sense that
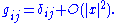
In fact, by taking the Taylor expansion of the metric applied to a Jacobi field
Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
along a radial geodesic in the normal coordinate system, one has
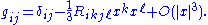
In these coordinates, the metric volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
then has the following expansion at p:
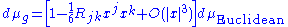
which follows by expanding the square root of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric.
Thus, if the Ricci curvature Ric(ξ,ξ) is positive in the direction of a vector ξ,
the conical region in M swept out by a tightly focused family of
short geodesic segments emanating from p with initial velocity inside a small cone around ξ
will have smaller volume than the corresponding conical region in Euclidean space, just as the surface a small spherical wedge
Spherical wedge
In geometry, a spherical wedge or ungula is a portion of a ball bounded by two plane semidisks and a spherical lune . The angle between the radii lying within the bounding semidisks is the dihedral angle of the wedge α...
has lesser area than a corresponding circular sector. Similarly, if the Ricci curvature is negative in the direction of a given vector ξ, such a conical region in the manifold will instead have larger volume than it would in Euclidean space.
The Ricci curvature is essentially an average of curvatures in the planes including ξ. Thus if a cone emitted with an initially circular (or spherical) cross-section becomes distorted into an ellipse (ellipsoid), it is possible for the volume distortion to vanish if the distortions along the principal axes counteract one another. The Ricci curvature would then vanish along ξ. In physical applications, the presence of a nonvanishing sectional curvature does not necessarily indicate the presence of any mass locally; if an initially circular cross-section of a cone of world-lines later becomes elliptical, without changing its volume, then this is due to tidal effects from a mass at some other location.
Applications
Ricci curvature plays an important role in general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, where it is the key term in the Einstein field equations.
Ricci curvature also appears in the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
equation, where a time-dependent Riemannian
metric is deformed in the direction of minus its Ricci curvature. This system of partial differential equations is a non-linear analog of the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, and was first
introduced by Richard Hamilton
Richard Hamilton (professor)
Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
in the early 1980s. Since heat tends to spread through a solid until the body reaches an equilibrium state of constant temperature, Ricci flow may be hoped to produce an equilibrium geometry for a manifold for which the Ricci curvature is constant. Recent contributions to the subject due to Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
now show that this program works well enough in dimension three to lead to a complete classification of compact 3-manifolds, along lines
first conjectured by William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
in the 1970s.
On a Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, the Ricci curvature determines the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the manifold (mod torsion). However, the Ricci curvature has no analogous topological interpretation
on a generic Riemannian manifold.
Global geometry and topology
Here is a short list of global results concerning manifolds with positive Ricci curvature; see also classical theorems of Riemannian geometry. Briefly, positive Ricci curvature of a Riemannian manifold has strong topological consequences, while (for dimension at least 3), negative Ricci curvature has no topological implications. (The Ricci curvature is said to be positive if the Ricci curvature function Ric(ξ,ξ) is positive on the set of non-zero tangent vectors ξ.) Some results are also known for pseudo-Riemannian manifolds.- Myers' theorem states that if the Ricci curvature is bounded from below on a complete Riemannian manifold by
, then the manifold has diameter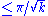 
, with equality only if the manifold is isometricIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to a sphere of a constant curvature k. By a covering-space argument, it follows that any compact manifold of positive Ricci curvature must have finite fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
. - The Bishop–Gromov inequalityBishop–Gromov inequalityIn mathematics, the Bishop–Gromov inequality is a comparison theorem in Riemannian geometry, named after Richard L. Bishop and Mikhail Gromov. It is closely related to Myers' theorem, and is the key point in the proof of Gromov's compactness theorem....
states that if a complete m-dimensional Riemannian manifold has non-negative Ricci curvature, then the volume of a ball is smaller or equal to the volume of a ball of the same radius in Euclidean m-space. Moreover, if
denotes the volume of the ball with center p and radius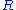 
in the manifold and 
denotes the volume of the ball of radius R in Euclidean m-space then function 
is nonincreasing. (The last inequality can be generalized to arbitrary curvature bound and is the key point in the proof of Gromov's compactness theoremGromov's compactness theorem (geometry)In Riemannian geometry, Gromov's compactness theorem states thatthe set of Riemannian manifolds of a given dimension, with Ricci curvature ≥ c and diameter ≤ D is relatively compact in the Gromov-Hausdorff metric. It was proved by Mikhail Gromov....
.) - The Cheeger-Gromoll splitting theorem states that if a complete Riemannian manifold with
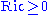contains a line, meaning a geodesic γ such that 
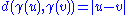for all 
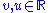, then it is isometric to a product space 
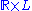. Consequently, a complete manifold of positive Ricci curvature can have at most one topological end. The theorem is also true under some additional hypotheses for complete Lorentzian manifolds (of metric signature (+−−...)) with non-negative Ricci tensor .
These results show that positive Ricci curvature has strong topological consequences. By contrast, excluding the case of surfaces, negative
Ricci curvature is now known to have no topological implications; has shown that any manifold of dimension greater than two admits a Riemannian metric of negative Ricci curvature. (For surfaces, negative Ricci curvature implies negative sectional curvature; but the point
is that this fails rather dramatically in all higher dimensions.)
Behavior under conformal rescaling
If you change the metric g by multiplying it by a conformal factor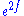, the Ricci tensor of the new, conformally related metric 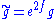is given by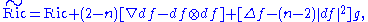where Δ = d∗d is the (positive spectrum) Hodge Laplacian, i.e., the opposite of the usual trace of the Hessian.
In particular, given a point p in a Riemannian manifold, it is always possible to find metrics conformal to the given metric g for which the Ricci tensor vanishes at p. Note, however, that this is only pointwise assertion; it is usually impossible to make the Ricci curvature vanish identically on the entire manifold by a conformal rescaling.
For two dimensional manifolds, the above formula shows that if f is a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
, then the conformal scaling g e2ƒg does not change the Ricci curvature.
Trace-free Ricci tensor
In Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the trace-free Ricci tensor of a pseudo-Riemannian
manifold
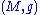is the tensor defined bywhere
is the Ricci tensor, 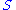is the scalar curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
,
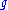is the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, and
is the dimension of .The name of this object reflects the fact that its trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
automatically vanishes:
If n
3, the trace-free Ricci tensor vanishes identically if and only if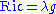for some constant
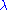.In mathematics, this is the condition for
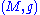to be an Einstein manifoldEinstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
. In physics, this equation
states that
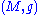is a solution of Einstein's vacuum fieldequations with cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
.
Kähler manifolds
On a Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
X, the Ricci curvature determines the curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
of the canonical line bundle
Canonical bundle
In mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
. The canonical line bundle is the top exterior power of the bundle of holomorphic Kähler differential
Kähler differential
In mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
s:
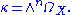
The Levi-Civita connection corresponding to the metric on X gives rise to a connection on κ. The curvature of this connection is the two form defined by
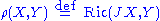
where J is the complex structure map of the Kähler manifold. The Ricci form is a closed two-form. Its cohomology class is, up to a real constant factor, the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the canonical bundle, and is therefore a topological invariant of X (for X compact) in the sense that it depends only on the topology of X and the homotopy class of the complex structure.
Conversely, the Ricci form determines the Ricci tensor by
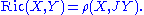
In local holomorphic coordinates zα, the Ricci form is given by
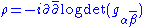
where
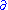is the Dolbeault operator and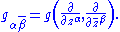If the Ricci tensor vanishes, then the canonical bundle is flat, so the structure group
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
can be locally reduced to a subgroup of the special linear group SL(n,C). However, Kähler manifolds already possess holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
in U(n), and so the (restricted) holonomy of a Ricci flat Kähler manifold is contained in SU(n). Conversely, if the (restricted) holonomy of a 2n-dimensional Riemannian manifold is contained in SU(n), then the manifold is a Ricci-flat Kähler manifold .
Generalization to affine connections
The Ricci tensor can also be generalized to arbitrary affine connectionAffine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
s, where it is an invariant that plays an especially important role in the study of the projective geometry
Projective differential geometry
In mathematics, projective differential geometry is the study of differential geometry, from the point of view of properties that are invariant under the projective group. This is a mixture of attitudes from Riemannian geometry, and the Erlangen program....
(geometry associated to unparameterized geodesics) . If
denotes an affine connection, then the curvature tensor 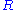is the 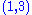tensor defined byfor any vector fields
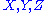. The Ricci tensor is defined to be the trace:In this more general situation, the Ricci tensor is symmetric if and only if there exists a parallel volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
for the connection.
See also
- Curvature of Riemannian manifoldsCurvature of Riemannian manifoldsIn mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
- Scalar curvatureScalar curvatureIn Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
- Ricci decompositionRicci decompositionIn semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
- Ricci-flat manifoldRicci-flat manifoldIn mathematics, Ricci-flat manifolds are Riemannian manifolds whose Ricci curvature vanishes. In physics, they represent vacuum solutions to the analogues of Einstein's equations for Riemannian manifolds of any dimension, with vanishing cosmological constant...
- Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
External links
- Z. Shen ,C. Sormani "The Topology of Open Manifolds with Nonnegative Ricci Curvature" (a survey)
- G. Wei, "Manifolds with A Lower Ricci Curvature Bound" (a survey)