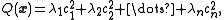Principal axis theorem
Encyclopedia
In the mathematical
fields of geometry
and linear algebra
, a principal axis is a certain line in a Euclidean space
associated to an ellipsoid or hyperboloid, generalizing the major and minor axes of an ellipse
. The principal axis theorem states that the principal axes are perpendicular, and gives a constructive procedure for finding them.
Mathematically, the principal axis theorem is a generalization of the method of completing the square
from elementary algebra
. In linear algebra
and functional analysis
, the principal axis theorem is a geometrical counterpart of the spectral theorem
. It has applications to the statistics
of principal components analysis
and the singular value decomposition
. In physics
, the theorem is fundamental to the study of angular momentum
.
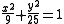
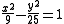
define, respectively, an ellipse and a hyperbola. In each case, the x and y axes are the principal axes. This is easily seen, given that there are no cross-terms involving products xy in either expression. However, the situation is more complicated for equations like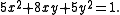
Here some method is required to determine whether this is an ellipse or a hyperbola. The basic observation is that if, by completing the square, the expression can be reduced to a sum of two squares then it defines an ellipse, whereas if it reduces to a difference of two squares then it is the equation of a hyperbola:
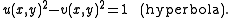
Thus, in our example expression, the problem is how to absorb the coefficient of the cross-term 8xy into the functions u and v. Formally, this problem is similar to the problem of matrix diagonalization, where one tries to find a suitable coordinate system in which the matrix of a linear transformation is diagonal. The first step is to find a matrix in which the technique of diagonalization can be applied.
The trick is to write the equation in the following form: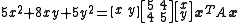
where the cross-term has been split into two equal parts. The matrix A in the above decomposition is a symmetric matrix. In particular, by the spectral theorem
, it has real eigenvalues and is diagonalizable by an orthogonal matrix
(orthogonally diagonalizable).
To orthogonally diagonalize A, one must first find its eigenvalues, and then find an orthonormal eigenbasis. Calculation reveals that the eigenvalues of A are
with corresponding eigenvectors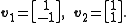
Dividing these by their respective lengths yields an orthonormal eigenbasis: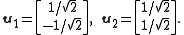
Now the matrix S = [u1 u2] is an orthogonal matrix, since it has orthonormal columns, and A is diagonalized by: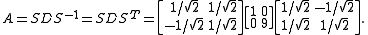
This applies to the present problem of "diagonalizing" the equation through the observation that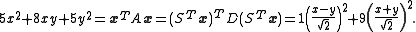
Thus, the equation is that of an ellipse, since it is the sum of two squares.
It is tempting to simplify this expression by pulling out factors of 2. However, it is important not to do this. The quantities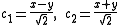
have a geometrical meaning. They determine an orthonormal coordinate system on R2. In other words, they are obtained from the original coordinates by the application of a rotation (and possibly a reflection). Consequently, one may use the c1 and c2 coordinates to make statements about length and angles (particularly length), which would otherwise be more difficult in a different choice of coordinates (by rescaling them, for instance). For example, the maximum distance from the origin on the ellipse c12 + 9c22 = 1 occurs when c2=0, so at the points c1=±1. Similarly, the minimum distance is where c2=±1/3.
It is possible now to read off the major and minor axes of this ellipse. These are precisely the individual eigenspaces of the matrix A, since these are where c2 = 0 or c1=0. Symbolically, the principal axes are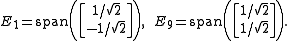
To summarize:
Using this information, it is possible to attain a clear geometrical picture of the ellipse: to graph it, for instance.
of degree 2. Any quadratic form can be put in the form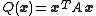
where A is a symmetric matrix.
The first part of the theorem is contained in the following statements guaranteed by the spectral theorem:
In particular, A is orthogonally diagonalizable, since one may take a basis of each eigenspace and apply the Gram-Schmidt process separately within the eigenspace to obtain an orthonormal eigenbasis.
For the second part, suppose that the eigenvalues of A are λ1, ..., λn (possibly repeated according to their algebraic multiplicities) and the corresponding orthonormal eigenbasis is u1,...,un. Then
where the ci are the coordinates with respect to the given eigenbasis. Furthermore,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
fields of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a principal axis is a certain line in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
associated to an ellipsoid or hyperboloid, generalizing the major and minor axes of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. The principal axis theorem states that the principal axes are perpendicular, and gives a constructive procedure for finding them.
Mathematically, the principal axis theorem is a generalization of the method of completing the square
Completing the square
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
from elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the principal axis theorem is a geometrical counterpart of the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. It has applications to the statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
of principal components analysis
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
and the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the theorem is fundamental to the study of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
Motivation
The equations in the Cartesian plane R2: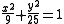
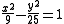
define, respectively, an ellipse and a hyperbola. In each case, the x and y axes are the principal axes. This is easily seen, given that there are no cross-terms involving products xy in either expression. However, the situation is more complicated for equations like
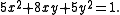
Here some method is required to determine whether this is an ellipse or a hyperbola. The basic observation is that if, by completing the square, the expression can be reduced to a sum of two squares then it defines an ellipse, whereas if it reduces to a difference of two squares then it is the equation of a hyperbola:

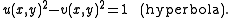
Thus, in our example expression, the problem is how to absorb the coefficient of the cross-term 8xy into the functions u and v. Formally, this problem is similar to the problem of matrix diagonalization, where one tries to find a suitable coordinate system in which the matrix of a linear transformation is diagonal. The first step is to find a matrix in which the technique of diagonalization can be applied.
The trick is to write the equation in the following form:
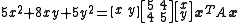
where the cross-term has been split into two equal parts. The matrix A in the above decomposition is a symmetric matrix. In particular, by the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, it has real eigenvalues and is diagonalizable by an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(orthogonally diagonalizable).
To orthogonally diagonalize A, one must first find its eigenvalues, and then find an orthonormal eigenbasis. Calculation reveals that the eigenvalues of A are

with corresponding eigenvectors
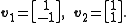
Dividing these by their respective lengths yields an orthonormal eigenbasis:
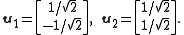
Now the matrix S = [u1 u2] is an orthogonal matrix, since it has orthonormal columns, and A is diagonalized by:
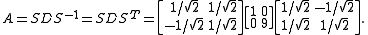
This applies to the present problem of "diagonalizing" the equation through the observation that
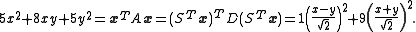
Thus, the equation is that of an ellipse, since it is the sum of two squares.
It is tempting to simplify this expression by pulling out factors of 2. However, it is important not to do this. The quantities
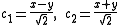
have a geometrical meaning. They determine an orthonormal coordinate system on R2. In other words, they are obtained from the original coordinates by the application of a rotation (and possibly a reflection). Consequently, one may use the c1 and c2 coordinates to make statements about length and angles (particularly length), which would otherwise be more difficult in a different choice of coordinates (by rescaling them, for instance). For example, the maximum distance from the origin on the ellipse c12 + 9c22 = 1 occurs when c2=0, so at the points c1=±1. Similarly, the minimum distance is where c2=±1/3.
It is possible now to read off the major and minor axes of this ellipse. These are precisely the individual eigenspaces of the matrix A, since these are where c2 = 0 or c1=0. Symbolically, the principal axes are
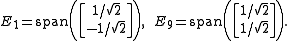
To summarize:
- The equation is for an ellipse, since both eigenvalues are positive. (Otherwise, if one were positive and the other negative, it would be a hyperbola.)
- The principal axes are the lines spanned by the eigenvectors.
- The minimum and maximum distances to the origin can be read off the equation in diagonal form.
Using this information, it is possible to attain a clear geometrical picture of the ellipse: to graph it, for instance.
Formal statement
The principal axis theorem applies to quadratic forms in Rn; that is polynomials Q(x) which are homogeneousHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree 2. Any quadratic form can be put in the form
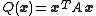
where A is a symmetric matrix.
The first part of the theorem is contained in the following statements guaranteed by the spectral theorem:
- The eigenvalues of A are real.
- A is diagonalizable, and the eigenspaces of A are mutually orthogonal.
In particular, A is orthogonally diagonalizable, since one may take a basis of each eigenspace and apply the Gram-Schmidt process separately within the eigenspace to obtain an orthonormal eigenbasis.
For the second part, suppose that the eigenvalues of A are λ1, ..., λn (possibly repeated according to their algebraic multiplicities) and the corresponding orthonormal eigenbasis is u1,...,un. Then
where the ci are the coordinates with respect to the given eigenbasis. Furthermore,
- The i-th principal axis is the line determined by the n-1 equations cj = 0, j ≠ i. This axis is the span of the vector ui.