Shape of the Universe - AbsoluteAstronomy.com

The shape of the universe is a matter of debate in physical cosmology

Physical cosmology

Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...

over the local and global geometry of the universe

Universe

The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...

which considers both curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

and topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, though, strictly speaking, it goes beyond both. In practice, more formally, the debate seeks a 3-manifold

3-manifold

In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...

that corresponds to the spatial section (in comoving coordinates) of the 4-dimensional space-time

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

of the universe.

The Wilkinson Microwave Anisotropy Probe

Wilkinson Microwave Anisotropy Probe

The Wilkinson Microwave Anisotropy Probe — also known as the Microwave Anisotropy Probe , and Explorer 80 — is a spacecraft which measures differences in the temperature of the Big Bang's remnant radiant heat — the Cosmic Microwave Background Radiation — across the full sky. Headed by Professor...

(WMAP) has confirmed that the universe is flat with only a 0.5% margin of error. Within the Friedmann-Lemaître-Robertson-Walker (FLRW) model, the presently most popular shape of the Universe found to fit observational data according to cosmologists is the infinite flat model, while other FLRW models that fit the data include the Poincaré dodecahedral space and the Picard horn

Picard horn

A Picard horn, also called the Picard topology or Picard model, is a theoretical model for theshape of the Universe. It is a horn topology, meaning it has hyperbolic geometry ....

Introduction

Consideration of the shape of the universe can be split into two; local geometry, which relates especially to the curvature of the universe, especially in the observable universe

Observable universe

In Big Bang cosmology, the observable universe consists of the galaxies and other matter that we can in principle observe from Earth in the present day, because light from those objects has had time to reach us since the beginning of the cosmological expansion...

, and global geometry, which relates to the topology of the universe as a whole, measurement of which may not be within our ability. If the observable universe encompasses the entire universe, we may determine the global structure by observation. If the observable universe is smaller than the entire universe (in some models it is many orders of magnitude smaller or even infinitesimal), observation is limited to a part of the whole. Possibly the universe is small in some dimensions and not in others (like a cylinder). If a small closed loop, one would see multiple images of an object in the sky, although not necessarily of the same age.

Cosmologists normally work with a given space-like slice of spacetime called the comoving coordinates

Comoving distance

In standard cosmology, comoving distance and proper distance are two closely related distance measures used by cosmologists to define distances between objects...

, the existence of a preferred set of which is possible and widely accepted in present-day physical cosmology. The section of spacetime that can be observed is the backward light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

(all points within the cosmic light horizon, given time to reach a given observer), while the related term Hubble volume

Hubble volume

In cosmology, the Hubble volume, or Hubble sphere, is the region of the Universe surrounding an observer beyond which objects recede from the observer at a rate greater than the speed of light, due to the expansion of the Universe....

can be used to describe either the past light cone or comoving space up to the surface of last scattering. To speak of "the shape of the universe (at a point in time)" is ontologically naive from the point of view of special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

alone: due to the relativity of simultaneity

Relativity of simultaneity

In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...

we cannot speak of different points in space as being "at the same point in time" nor, therefore, of "the shape of the universe at a point in time".

Local geometry (spatial curvature)

The local geometry is the curvature describing any arbitrary point in the observable universe (averaged on a sufficiently large scale). Many astronomical observations, such as those from supernovae and the Cosmic Microwave Background (CMB) radiation, show the observable universe to be very close to homogeneous and isotropic and infer it to be accelerating.

FLRW model of the universe

In General Relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, this is modelled by the Friedmann-Lemaître-Robertson-Walker (FLRW) model. This model, which can be represented by the Friedmann equations

Friedmann equations

The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity...

, provides a curvature (often referred to as geometry) of the universe based on the mathematics of fluid dynamics

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

, i.e. it models the matter within the universe as a perfect fluid. Although stars and structures of mass can be introduced into an "almost FLRW" model, a strictly FLRW model is used to approximate the local geometry of the observable universe.

Another way of saying this is that if all forms of dark energy

Dark energy

In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...

are ignored, then the curvature of the universe can be determined by measuring the average density of matter within it, assuming that all matter is evenly distributed (rather than the distortions caused by 'dense' objects such as galaxies).

This assumption is justified by the observations that, while the universe is "weakly" inhomogeneous

Homogeneity (physics)

In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...

and anisotropic

Anisotropy

Anisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...

(see the large-scale structure of the cosmos), it is on average homogeneous and isotropic.

The homogeneous and isotropic universe allows for a spatial geometry with a constant curvature

Constant curvature

In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...

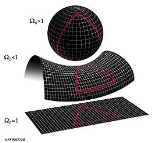
. One aspect of local geometry to emerge from General Relativity and the FLRW model is that the density parameter, Omega (Ω), is related to the curvature of space. Omega is the average density of the universe divided by the critical energy density, i.e. that required for the universe to be flat (zero curvature).

The curvature of space is a mathematical description of whether or not the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

is valid for spatial coordinates. In the latter case, it provides an alternative formula for expressing local relationships between distances:

If the curvature is zero, then Ω = 1, and the Pythagorean theorem is correct;
If Ω > 1, there is positive curvature; and
if Ω < 1 there is negative curvature.

In the last two cases, the Pythagorean theorem is invalid (but discrepancies are only detectable in triangles whose sides' lengths are of cosmological scale).

If you measure the circumferences of circles of steadily larger diameters and divide the former by the latter, all three geometries give the value π for small enough diameters but the ratio departs from π for larger diameters unless Ω = 1:

For Ω > 1 (the sphere, see diagram) the ratio falls below π: indeed, a great circle on a sphere has circumference only twice its diameter.
For Ω < 1 the ratio rises above π.

Astronomical measurements of both matter-energy density of the universe and spacetime intervals using supernova events constrain the spatial curvature to be very close to zero, although they do not constrain its sign. This means that although the local geometries of spacetime are generated by the theory of relativity

Theory of relativity

The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....

based on spacetime intervals, we can approximate 3-space by the familiar Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

Possible local geometries

There are three categories for the possible spatial geometries of constant curvature

Constant curvature

, depending on the sign of the curvature. If the curvature is exactly zero, then the local geometry is flat; if it is positive, then the local geometry is spherical, and if it is negative then the local geometry is hyperbolic.

The geometry of the universe is usually represented in the system of comoving coordinates, according to which the expansion of the universe can be ignored. Comoving coordinates form a single frame of reference

Frame of reference

A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...

according to which the universe has a static geometry of three spatial dimensions.

Under the assumption that the universe is homogeneous and isotropic, the curvature of the observable universe, or the local geometry, is described by one of the three "primitive" geometries (in mathematics these are called the model geometries

Geometrization conjecture

Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...

3-dimensional Flat Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

, generally notated as E³
3-dimensional spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....

with a small curvature, often notated as S³
3-dimensional hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

with a small curvature

Even if the universe is not exactly spatially flat, the spatial curvature is close enough to zero to place the radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

at approximately the horizon of the observable universe or beyond.

Global geometry

Global geometry covers the geometry, in particular the topology

Topology

, of the whole universe—both the observable universe and beyond. While the local geometry does not determine the global geometry completely, it does limit the possibilities, particularly a geometry of a constant curvature.
For this discussion, the universe is taken to be a geodesic manifold, free of topological defects; relaxing either of these complicates the analysis considerably.

In general, local to global theorems in Riemannian geometry

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...

relate the local geometry to the global geometry. If the local geometry has constant curvature, the global geometry is very constrained, as described in Thurston geometries

Geometrization conjecture

.

A global geometry is also called a topology, as a global geometry is a local geometry plus a topology, but this terminology is misleading because a topology does not give a global geometry: for instance, Euclidean 3-space and hyperbolic 3-space

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

have the same topology but different global geometries.

Two strongly overlapping investigations within the study of global geometry are whether the universe:

Is infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

in extent or, more generally, is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

;
Has a simply or non-simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...

topology.

Detection

For a flat spatial geometry, the scale of any properties of the topology is arbitrary and may or may not be directly detectable. For spherical and hyperbolic spatial geometries, the curvature gives a scale (either by using the radius of curvature or its inverse

Multiplicative inverse

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

), a fact noted by Carl Friedrich Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

in an 1824 letter to Franz Taurinus

Franz Taurinus

Franz Adolph Taurinus was a German mathematician who was famous for his work on non-Euclidean geometry.-External links:...

.

The probability of detection of the topology by direct observation depends on the spatial curvature: a small curvature of the local geometry, with a corresponding radius of curvature greater than the observable horizon, makes the topology difficult or impossible to detect if the curvature is hyperbolic. A spherical geometry with a small curvature (large radius of curvature) does not make detection difficult.

Analysis of data from WMAP

Wilkinson Microwave Anisotropy Probe

implies that on the scale to the surface of last scattering, the density parameter of the Universe is within about 2% of the value representing spatial flatness

Euclidean geometry

Compactness of the global shape

Formally, the question of whether the universe is infinite or finite is whether it is an unbounded or bounded metric space. An infinite universe (unbounded metric space) means that there are points arbitrarily far apart: for any distance d, there are points that are of a distance at least d apart. A finite universe is a bounded metric space, where there is some distance d such that all points are within distance d of each other. The smallest such d is called the diameter of the universe, in which case the universe has a well-defined "volume" or "scale."

A compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

is a stronger condition: in the context of Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

s, it is equivalent to being bounded and geodesically complete. If we assume that the universe is geodesically complete, then boundedness and compactness are equivalent (by the Hopf–Rinow theorem

Hopf–Rinow theorem

In mathematics, the Hopf–Rinow theorem is a set of statements about the geodesic completeness of Riemannian manifolds. It is named after Heinz Hopf and his student Willi Rinow .-Statement of the theorem:...

), and they are thus used interchangeably, if completeness is understood.

If the spatial geometry is spherical

Spherical 3-manifold

In mathematics, a spherical 3-manifold M is a 3-manifold of the formM=S^3/\Gammawhere \Gamma is a finite subgroup of SO acting freely by rotations on the 3-sphere S^3. All such manifolds are prime, orientable, and closed...

, the topology is compact. For a flat or a hyperbolic spatial geometry, the topology can be either compact or infinite: for example, Euclidean space is flat and infinite, but the torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

is flat and compact.

In cosmological models (geometric 3-manifolds), a compact space is either a spherical geometry, or has infinite fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

(and thus is called "multiply connected", or more strictly non-simply connected), by general results on geometric 3-manifolds.

Compact geometries can be visualized by means of closed geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s: on a sphere, a straight line, when extended far enough in the same direction, will reach the starting point.

Note that on a compact geometry, not every straight line comes back to its starting point. For instance, a line of irrational slope on a torus never returns to its origin. Conversely, a non-compact geometry can have closed geodesics: on an infinite cylinder, which is a non-compact flat geometry, a loop around the cylinder is a closed geodesic.

If the geometry of the universe is not compact, then it is infinite in extent with infinite paths of constant direction that, generally do not return and the space has no definable volume, such as the Euclidean plane.

Open or closed

When cosmologists speak of the universe as being "open" or "closed", they most commonly are referring to whether the curvature is negative or positive. These meanings of open and closed, and the mathematical meanings, give rise to ambiguity because the terms can also refer to a closed manifold

Closed manifold

In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....

i.e. compact without boundary, not to be confused with a closed set

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

. With the former definition, an "open universe" may either be an open manifold, i.e. one that is not compact and without boundary, or a closed manifold, while a "closed universe" is necessarily a closed manifold.

In the Friedmann-Lemaître-Robertson-Walker (FLRW) model the universe is considered to be without boundaries, in which case "compact universe" could describe a universe that is a closed manifold.

The latest research shows that even the most powerful future experiments (like SKA, Planck..) will not be able to distinguish between flat, open and closed universe if the true value of cosmological curvature parameter is smaller than 10⁻⁴. If the true value of the cosmological curvature parameter is larger than 10⁻³ we will be able to distinguish between these three models even now.

Flat universe

In a flat universe, all of the local curvature and local geometry is flat. It is generally assumed that it is described by a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, although there are some spatial geometries that are flat and bounded in one or more directions (like the surface of a cylinder, for example).

The alternative two-dimensional spaces with a Euclidean metric are the cylinder

Cylinder (geometry)

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

and the Möbius strip

Möbius strip

The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...

, which are bounded in one direction but not the other, and the torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

and Klein bottle

Klein bottle

In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...

, which are compact.

In three dimensions, there are 10 finite closed flat 3-manifolds, of which 6 are orientable and 4 are non-orientable. The most familiar is the 3-Torus. See the doughnut theory of the universe

Doughnut theory of the universe

The doughnut theory of the universe is an informal description of the theory that the shape of the universe is a three-dimensional torus. The name comes from the shape of a doughnut, whose surface has the topology of a two-dimensional torus....

In the absence of dark energy, a flat universe expands forever but at a continually decelerating rate, with expansion asymptotically approaching some fixed rate. With dark energy, the expansion rate of the universe initially slows down, due to the effect of gravity, but eventually increases. The ultimate fate of the universe

Ultimate fate of the universe

The ultimate fate of the universe is a topic in physical cosmology. Many possible fates are predicted by rival scientific theories, including futures of both finite and infinite duration....

is the same as that of an open universe.

A flat universe can have zero total energy

Zero-energy Universe

The zero-energy universe hypothesis states that the total amount of energy in the universe is exactly zero. When the energy of the universe is considered from a pseudo-tensor point of view, zero values are obtained in the resulting calculations...

and thus can come from nothing

Nothing comes from nothing

Nothing comes from nothing is a philosophical expression of a thesis first argued by Parmenides. It is associated with ancient Greek cosmology, such as presented not just in the opus of Homer and Hesiod, but also in virtually every philosophical system – there is no time interval in which a...

Spherical universe

A positively curved universe is described by spherical geometry

Spherical geometry

Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....

, and can be thought of as a three-dimensional hypersphere

Hypersphere

In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...

, or some other spherical 3-manifold

Spherical 3-manifold

(such as the Poincaré dodecahedral space), all of which are quotients of the 3-sphere.

Analysis of data from the Wilkinson Microwave Anisotropy Probe (WMAP) looks for multiple "back-to-back" images of the distant universe in the cosmic microwave background radiation. It may be possible to observe multiple images of a given object, if the light it emits has had sufficient time to make one or more complete circuits of a bounded universe. Current results and analysis do not rule out a bounded global geometry (i.e. a closed universe), but they do confirm that the spatial curvature is small, just as the spatial curvature of the surface of the Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

is small compared to a horizon of a thousand kilometers or so. If the universe is bounded, this does not imply anything about the sign or zeroness of its curvature.

In a closed universe lacking the repulsive effect of dark energy

Dark energy

, gravity eventually stops the expansion of the universe, after which it starts to contract until all matter in the observable universe collapses to a point, a final singularity termed the Big Crunch

Big Crunch

In physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...

, by analogy with Big Bang. However, if the universe has a large amount of dark energy (as suggested by recent findings), then the expansion of the universe could continue forever.

Based on analyses of the WMAP data, cosmologists during 2004–2006 focused on the
Poincaré dodecahedral space (PDS), but horn topologies (which are hyperbolic) were also deemed compatible with the data.

Hyperbolic universe

A hyperbolic universe is described by hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

, and can be thought of locally as a three-dimensional analog of an infinitely extended saddle shape. There are a great variety of hyperbolic 3-manifold

Hyperbolic 3-manifold

A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...

s, and their classification is not completely understood. For hyperbolic local geometry, many of the possible three-dimensional spaces are informally called horn topologies, so called because of the shape of the pseudosphere

Pseudosphere

In geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid....

, a canonical model of hyperbolic geometry.

Spherical Expanding Universe (Milne model
Milne model
The Milne model was a special relativistic cosmological model proposed by Edward Arthur Milne in 1935. It is mathematically equivalent to a special case of the FLRW model in the limit of zero energy density , and it obeys the cosmological principle...

)

If the Universe is contained within an ever expanding sphere (which may have started from a single point), it can still appear infinite for all practical purposes. Because of length contraction

Length contraction

In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...

the galaxies further away, which are travelling away from the observer the fastest, will appear smaller. In this way an infinite Universe fits within a finite sphere as long as the sphere is expanding continually. The question of whether the Universe is infinite can depend on the coordinate system used. For example, you could choose a coordinate system in which the galaxies are equally spaced out and don't have length contraction

Length contraction

, in which case the Universe could be said to be infinite in size.
Whichever galaxy the observer is on, the other galaxies moving away from it will appear length contracted. An observer can never get to the edge of the Universe if it is expanding at the speed of light. At the edge of the sphere matter becomes infinitely dense, but because it is moving away from the observer close to the speed of light due to time dilation

Time dilation

In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...

its effect on the rest of the Universe is negligible.
As the spherical Universe expands, matter that was near the edge is now in the middle of the sphere.

Proposed models

Various models have been proposed for the global geometry of the universe. In addition to the primitive geometries, these proposals include the:

Poincaré dodecahedral space, a positively curved space, colloquially described as "soccer ball shaped", as it is the quotient of the 3-sphere by the binary icosahedral group, which is very close to icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...

, the symmetry of a soccer ball. This was proposed by Jean-Pierre Luminet
Jean-Pierre Luminet
Jean-Pierre Luminet is a French astrophysicist, specialized in black holes and cosmology. He works as research director for the CNRS , and is a member of the Laboratoire Univers et Théories of the observatory of Paris-Meudon.The asteroid 5523 Luminet, was named after him .-Timeline:* 2003 - An...

and colleagues in 2003 and an optimal orientation on the sky for the model was estimated in 2008.

Picard horn
Picard horn
A Picard horn, also called the Picard topology or Picard model, is a theoretical model for theshape of the Universe. It is a horn topology, meaning it has hyperbolic geometry ....

, a negatively curved space, colloquially described as "funnel-shaped", for the horn geometry.

External links

Geometry of the Universe
A cosmic hall of mirrors - physicsworld (26 September 2005)
Universe is Finite, "Soccer Ball"-Shaped, Study Hints. Possible wrap-around dodecahedral shape of the universe
Classification of possible universes in the Lambda-CDM model.
Closed hyperbolic universe.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.