Holonomy - AbsoluteAstronomy.com

In differential geometry, the holonomy of a connection

Connection (mathematics)

In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...

on a smooth manifold is a general geometrical consequence of the curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

of the connection measuring the extent to which parallel transport

Parallel transport

In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...

around closed loops fails to preserve the geometrical data being transported. For flat connections, the associated holonomy is a type of monodromy

Monodromy

In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...

, and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features.

Any kind of connection on a manifold gives rise, through its parallel transport maps, to some notion of holonomy. The most common forms of holonomy are for connections possessing some kind of symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

. Important examples include: holonomy of the Levi-Civita connection

Levi-Civita connection

In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...

in Riemannian geometry

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...

(called Riemannian holonomy), holonomy of connections

Connection (vector bundle)

In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...

in vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

s, holonomy of Cartan connection

Cartan connection

In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...

s, and holonomy of connections

Connection (principal bundle)

In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...

in principal bundle

Principal bundle

In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...

s. In each of these cases, the holonomy of the connection can be identified with a Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

, the holonomy group. The holonomy of a connection is closely related to the curvature of the connection, via the Ambrose–Singer theorem.

The study of Riemannian holonomy has led to a number of important developments. The holonomy was introduced by in order to study and classify symmetric space

Symmetric space

A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...

s. It was not until much later that holonomy groups would be used to study Riemannian geometry in a more general setting. In 1952 Georges de Rham

Georges de Rham

Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...

proved the de Rham decomposition theorem, a principle for splitting a Riemannian manifold into a Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

of Riemannian manifolds by splitting the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

into irreducible spaces under the action of the local holonomy groups. Later, in 1953, M. Berger classified the possible irreducible holonomies. The decomposition and classification of Riemannian holonomy has applications to physics, and in particular to string theory

String theory

String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...

Holonomy of a connection in a vector bundle

Let E be a rank k vector bundle

Vector bundle

over a smooth manifold M and let ∇ be a connection

Connection (vector bundle)

on E. Given a piecewise

Piecewise

On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...

smooth loop

Loop (topology)

In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...

γ : [0,1] → M based at x in M, the connection defines a parallel transport

Parallel transport

map

. This map is both linear and invertible and so defines an element of GL(E_x). The holonomy group of ∇ based at x is defined as

The restricted holonomy group based at x is the subgroup

coming from contractible loops γ.

If M is connected

Connected space

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...

then the holonomy group depends on the basepoint x only up to

Up to

In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...

conjugation

Conjugacy class

In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

in GL(k, R). Explicitly, if γ is a path from x to y in M then

Choosing different identifications of E_x with R^k also gives conjugate subgroups. Sometimes, particularly in general or informal discussions (such as below), one may drop reference to the basepoint, with the understanding that the definition is good up to conjugation.

Some important properties of the holonomy group include:

Hol⁰(∇) is a connected, Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...

of GL(k, R).
Hol⁰(∇) is the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...

of Hol(∇).
There is a natural, surjective group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

π₁(M) → Hol(∇)/Hol⁰(∇) where π₁(M) is the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

of M which sends the homotopy class [γ] to the coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...

P_γ·Hol⁰(∇).
If M is simply connected then Hol(∇) = Hol⁰(∇).
∇ is flat (i.e. has vanishing curvature) if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

Hol⁰(∇) is trivial.

Holonomy of a connection in a principal bundle

The definition for holonomy of connections on principal bundles proceeds in parallel fashion. Let G be a Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

and P a principal G-bundle

Principal bundle

In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...

over a smooth manifold M which is paracompact. Let ω be a connection

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

on P. Given a piecewise smooth loop

Loop (topology)

In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...

γ : [0,1] → M based at x in M and a point p in the fiber over x, the connection defines a unique horizontal lift

such that

. The end point of the horizontal lift,

, will not generally be p but rather some other point p·g in the fiber over x. Define an equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

~ on P by saying that p ~ q if they can be joined by a piecewise smooth horizontal path in P.

The holonomy group of ω based at p is then defined as

The restricted holonomy group based at p is the subgroup

coming from horizontal lifts of contractible loops γ.

If M and P are connected

Connected space

then the holonomy group depends on the basepoint p only up to conjugation in G. Explicitly, if q is any other chosen basepoint for the holonomy, then there exists a unique g ∈ G such that q ~ p g. With this value of g,

In particular,

Moreover, if p ~ q then Hol_p(ω) = Hol_q(ω).
As above, sometimes one drops reference to the basepoint of the holonomy group, with the understanding that the definition is good up to conjugation.

Some important properties of the holonomy and restricted holonomy groups include:

Hol⁰_p(ω) is a connected Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...

of G.
Hol⁰_p(ω) is the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...

of Hol_p(ω).
There is a natural, surjective group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

π₁(M) → Hol_p(ω)/Hol⁰_p(ω).
If M is simply connected then Hol_p(ω) = Hol⁰_p(ω).
ω is flat (i.e. has vanishing curvature) if and only if Hol⁰_p(ω) is trivial.

Holonomy bundles

Let M be a connected paracompact smooth manifold and P a principal G-bundle with connection ω, as above. Let p ∈ P be an arbitrary point of the principal bundle. Let H(p) be the set of points in P which can be joined to p by a horizontal curve. Then it can be shown that H(p), with the evident projection map, is a principal bundle over M with structure group Hol⁰_p(ω). This principal bundle is called the holonomy bundle (through p) of the connection. The connection ω restricts to a connection on H(p), since its parallel transport maps preserve H(p). Thus H(p) is a reduced bundle for the connection. Furthermore, since no subbundle of H(p) is preserved by parallel transport, it is the minimal such reduction.

As with the holonomy groups, the holonomy bundle also transforms equivariantly within the ambient principal bundle P. In detail, if q ∈ P is another chosen basepoint for the holonomy, then there exists a unique g ∈ G such that q ~ p g (since, by assumption, M is path-connected). Hence H(q) = H(p) g. As a consequence, the induced connections on holonomy bundles corresponding to different choices of basepoint are compatible with one another: their parallel transport maps will differ by precisely the same element g.

Monodromy

The holonomy bundle H(p) is a principal bundle for Hol_p(ω), and so also admits an action of the restricted holonomy group Hol⁰_p(ω) (which is a normal subgroup of the full holonomy group). The discrete group Hol_p(ω)/Hol⁰_p(ω) is called the monodromy group of the connection; it acts on the quotient bundle H(p)/Hol⁰_p(ω). There is a surjective homomorphism φ : π₁(M) → Hol_p(ω)/Hol⁰_p(ω), so that φ(π₁(M)) acts on H(p)/Hol⁰_p(ω). This action of the fundamental group is a monodromy representation of the fundamental group.

Local and infinitesimal holonomy

If π : P → M is a principal bundle, and ω is a connection in P, then the holonomy of ω can be restricted to the fibre over an open subset of M. Indeed, if U is a connected open subset of M, then ω restricts to give a connection in the bundle π⁻¹U over U. The holonomy (resp. restricted holonomy) of this bundle will be denoted by Hol_p(ω, U) (resp. Hol_p⁰(ω, U)) for each p with π(p) ∈ U.

If U ⊂ V are two open sets containing π(p), then there is an evident inclusion

The local holonomy group at a point p is defined by

for any family of nested connected open sets U_k with

.

The local holonomy group has the following properties:

It is a connected Lie subgroup of the restricted holonomy group Hol_p⁰(ω).
Every point p has a neighborhood V such that Hol_p*(ω)=Hol_p⁰(ω,V). In particular, the local holonomy group depends only on the point p, and not the choice of sequence U_{k used to define it.}
The local holonomy is equivariant with respect to translation by elements of the structure group G of P; i.e., Hol_pg*(ω) = Ad(g⁻¹)Hol_{p*(ω) for all g ∈ G. (Note that, by property 1., the local holonomy group is a connected Lie subgroup of G, so the adjoint is well-defined.)}

The local holonomy group is not well-behaved as a global object. In particular, its dimension may fail to be constant. However, the following theorem holds:

If the dimension of the local holonomy group is constant, then the local and restricted holonomy agree: Hol_p*(ω) = Hol_p⁰(ω).

The infinitesimal holonomy is the Lie algebra of the restricted holonomy group.

Ambrose–Singer theorem

The Ambrose–Singer theorem relates the holonomy of a connection in a principal bundle

Connection (principal bundle)

In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...

with the curvature form

Curvature form

In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...

of the connection. To make this theorem plausible, consider the familiar case of an affine connection

Affine connection

In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...

(or a connection in the tangent bundle — the Levi-Civita connection, for example). The curvature arises when one travels around an infinitesimal parallelogram.

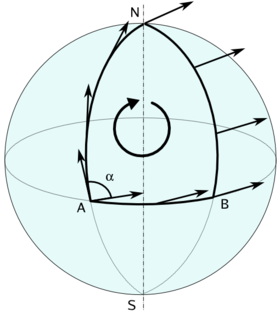
In detail, if σ : [0, 1] × [0, 1] → M is a surface in M parametrized by a pair of variables x and y, then a vector V may be transported around the boundary of σ: first along (x, 0), then along (1, y), followed by (x, 1) going in the negative direction, and then (0, y) back to the point of origin. This is a special case of a holonomy loop: the vector V is acted upon by the holonomy group element corresponding to the lift of the boundary of σ. The curvature enters explicitly when the parallelogram is shrunk to zero, by traversing the boundary of smaller parallelograms over [0, x] × [0, y]. This corresponds to taking a derivative of the parallel transport maps at x = y = 0:

where R is the curvature tensor

Curvature tensor

In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...

. So, roughly speaking, the curvature gives the infinitesimal holonomy over a closed loop (the infinitesimal parallelogram). More formally, the curvature is the differential of the holonomy action at the identity of the holonomy group. In other words, R(X, Y) is an element of the Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

of Hol_p(ω).

In general, consider the holonomy of a connection in a principal bundle P → M over P with structure group G. Denoting the Lie algebra of G by g, the curvature form

Curvature form

of the connection is a g-valued 2-form Ω on P. The Ambrose–Singer theorem states:

The Lie algebra of Hol_p(ω) is spanned by all the elements of g of the form Ω_q(X,Y) as q ranges over all points which can be joined to p by a horizontal curve (q ~ p), and X and Y are horizontal tangent vectors at q.

Alternatively, the theorem can be restated in terms of the holonomy bundle:

The Lie algebra of Hol_p(ω) is the subspace of g spanned by elements of the form Ω_q(X, Y) where q ∈ H(p) and X and Y are horizontal vectors at q.

Riemannian holonomy

The holonomy of a Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

(M, g) is just the holonomy group of the Levi-Civita connection

Levi-Civita connection

on the tangent bundle

Tangent bundle

to M. A 'generic' n-dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

al Riemannian manifold

Riemannian manifold

has an O(n)

Orthogonal group

In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...

holonomy, or SO(n) if it is orientable. Manifolds whose holonomy groups are proper subgroups of O(n) or SO(n) have special properties.

One of the earliest fundamental results on Riemannian holonomy is the theorem of , which asserts that the holonomy group is a closed Lie subgroup of O(n). In particular, it is compact.

Reducible holonomy and the de Rham decomposition

Let x ∈ M be an arbitrary point. Then the holonomy group Hol(M) acts on the tangent space T_xM. This action may either be irreducible as a group representation, or reducible in the sense that there is a splitting of T_xM into orthogonal subspaces T_xM = T′_xM ⊕ T′′_xM, each of which is invariant under the action of Hol(M). In the latter case, M is said to be reducible.

Suppose that M is a reducible manifold. Allowing the point x to vary, the bundles T′M and T′′M formed by the reduction of the tangent space at each point are smooth distributions which are integrable in the sense of Frobenius. The integral manifolds of these distributions are totally geodesic submanifolds. So M is locally a Cartesian product M′ × M′′. The (local) de Rham isomorphism follows by continuing this process until a complete reduction of the tangent space is achieved:

Let M be a simply connected Riemannian manifold, and TM = T⁽⁰⁾M ⊕ T⁽¹⁾M ⊕ ... ⊕ T^(k)M be the complete reduction of the tangent bundle under the action of the holonomy group. Suppose that T⁽⁰⁾M consists of vectors invariant under the holonomy group (i.e., such that the holonomy representation is trivial). Then locally M is isometric to a product

where V₀ is an open set in a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, and each V_i is an integral manifold for T⁽ⁱ⁾M. Furthermore, Hol(M) splits as a direct product of the holonomy groups of each M_i.

If, moreover, M is assumed to be geodesically complete, then the theorem holds globally, and each M_i is a geodesically complete manifold.

The Berger classification

In 1955, M. Berger gave a complete classification of possible holonomy groups for simply connected, Riemannian manifolds which are irreducible (not locally a product space) and nonsymmetric (not locally a Riemannian symmetric space

Riemannian symmetric space

In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...

). Berger's list is as follows:

Hol(g)	dim(M)	Type of manifold	Comments
SO(n)	n	Orientable manifold
U(n) Unitary group In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...	2n	Kähler manifold Kähler manifold In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...	Kähler
SU(n) Special unitary group The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...	2n	Calabi–Yau manifold	Ricci-flat, Kähler
Sp(n)·Sp(1)	4n	Quaternion-Kähler manifold Quaternion-Kähler manifold In differential geometry, a quaternion-Kähler manifold is a Riemannian manifold whose Riemannian holonomy group is a subgroup of Sp·Sp....	Einstein Einstein manifold In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
Sp(n) Symplectic group In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...	4n	Hyperkähler manifold Hyperkähler manifold In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...	Ricci-flat, Kähler
G₂	7	G₂ manifold G2 manifold In differential geometry, a G2 manifold is a seven-dimensional Riemannian manifold with holonomy group G2. The group G_2 is one of the five exceptional simple Lie groups...	Ricci-flat
Spin(7)	8	Spin(7) manifold	Ricci-flat

(Berger's original list also included the possibility of Spin(9) as a subgroup of SO(16). Riemannian manifolds with such holonomy were later shown independently by D. Alekseevski and Brown-Gray to be necessarily locally symmetric, i.e., locally isometric to the Cayley plane

Cayley plane

In mathematics, the Cayley plane OP2 is a projective plane over the octonions. It was discovered in 1933 by Ruth Moufang, and is named after Arthur Cayley ....

F₄/Spin(9) or locally flat. See below.) It is now known that all of these possibilities occur as holonomy groups of Riemannian manifolds. The last two exceptional cases were the most difficult to find. See G₂ manifold

G2 manifold

In differential geometry, a G2 manifold is a seven-dimensional Riemannian manifold with holonomy group G2. The group G_2 is one of the five exceptional simple Lie groups...

and Spin(7) manifold.

Note that Sp(n) ⊂ SU(2n) ⊂ U(2n) ⊂ SO(4n), so every hyperkähler manifold

Hyperkähler manifold

In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...

is a Calabi–Yau manifold, every Calabi–Yau manifold is a Kähler manifold

Kähler manifold

In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...

, and every Kähler manifold

Kähler manifold

is orientable.

The strange list above was explained by Simons's proof of Berger's theorem. A simple and geometric proof of Berger's theorem was given by Carlos Olmos in 2005. One first shows that if a Riemannian manifold is not a locally symmetric space and the reduced holonomy acts irreducibly on the tangent space, then it acts transitively on the unit sphere. The Lie groups acting transitively on spheres are known: they consist of the list above, together with 2 extra cases: the group Spin(9) acting on R¹⁶, and the group T·Sp(m) acting on R^4m. Finally one checks that the first of these two extra cases only occurs as a holonomy group for locally symmetric spaces (that are locally isomorphic to the Cayley projective plane), and the second does not occur at all as a holonomy group.

Berger's original classification also included non-positive-definite pseudo-Riemannian metric non-locally symmetric holonomy. That list consisted of SO(p,q) of signature (p,q), U(p,q) and SU(p,q) of signature (2p,2q), Sp(p,q) and Sp(p,q)·Sp(1) of signature (4p,4q), SO(n,C) of signature (n,n), SO(n,H) of signature (2n,2n), split G₂ of signature (4,3), G₂(C) of signature (7,7), Spin(4,3) of signature (4,4), Spin(7,C) of signature (7,7), Spin(5,4) of signature (8,8) and, lastly, Spin(9,C) of signature (16,16). The split and complexified Spin(9) are necessarily locally symmetric as above and should not have been on the list. The complexified holonomies SO(n,C), G₂(C), and Spin(7,C) may be realized from complexifying real analytic Riemannian manifolds. The last case, manifolds with holonomy contained in SO(n,H), were shown to be locally flat by R. McLean.

Riemannian symmetric spaces, which are locally isometric to homogeneous space

Homogeneous space

In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...

have local holonomy isomorphic to

. These too have been completely classified.

Finally, Berger's paper lists possible holonomy groups of manifolds with only a torsion-free

Torsion-free

In mathematics, the term torsion-free may refer to several unrelated notions:* In abstract algebra, a group is torsion-free if the only element of finite order is the identity....

affine connection

Affine connection

; this is discussed below.

Special holonomy and spinors

Manifolds with special holonomy play a fundamental role in the theory of spinor

Spinor

In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...

s, and particularly pure spinor

Pure spinor

In a field of mathematics known as representation theory pure spinors are spinor representations of the special orthogonal group that are annihilated by the largest possible subspace of the Clifford algebra. They were introduced by Élie Cartan in the 1930s to classify complex structures...

s. In particular, the following facts hold:

Hol(ω) ⊂ U(n) if and only if M admits a covariantly constant (or parallel) projective pure spinor field.
If M is a spin manifold
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....

, then Hol(ω) ⊂ SU(n) if and only if M admits a parallel pure spinor field. In fact, a parallel pure spinor field determines a canonical reduction of the structure group to SU(n).
If M is a seven-dimensional spin manifold, then M carries a non-trivial parallel spinor field if and only if the holonomy is contained in G₂.
If M is an eight-dimensional spin manifold, then M carries a non-trivial parallel spinor field if and only if the holonomy is contained in Spin(7).

The unitary and special unitary holonomies are often studied in connection with twistor theory

Twistor theory

In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...

, as well as in the study of almost complex structures.

Applications to string theory

Riemannian manifolds with special holonomy play an important role in string theory

String theory

compactifications

Compactification (physics)

In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....

. This is because special holonomy manifolds admit covariantly constant (parallel) spinor

Spinor

s and thus preserve some fraction of the original supersymmetry

Supersymmetry

In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...

. Most important are compactifications on Calabi–Yau manifolds with SU(2) or SU(3) holonomy. Also important are compactifications on G₂ manifold

G2 manifold

In differential geometry, a G2 manifold is a seven-dimensional Riemannian manifold with holonomy group G2. The group G_2 is one of the five exceptional simple Lie groups...

Affine holonomy

Affine holonomy groups are the groups arising as holonomies of torsion-free

Torsion-free

In mathematics, the term torsion-free may refer to several unrelated notions:* In abstract algebra, a group is torsion-free if the only element of finite order is the identity....

affine connection

Affine connection

s; those which are not Riemannian or pseudo-Riemannian holonomy groups are also known as non-metric holonomy groups. The deRham decomposition theorem does not apply to affine holonomy groups, so a complete classification is out of reach. However, it is still natural to classify irreducible affine holonomies.

On the way to his classification of Riemannian holonomy groups, Berger developed two criteria that must be satisfied by the Lie algebra of the holonomy group of a torsion-free affine connection which is not locally symmetric

Symmetric space

A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...

: one of them, known as Berger's first criterion, is a consequence of the Ambrose–Singer theorem, that the curvature generates the holonomy algebra; the other, known as Berger's second criterion, comes from the requirement that the connection should not be locally symmetric. Berger presented a list of groups acting irreducibly and satisfying these two criteria; this can be interpreted as a list of possibilities for irreducible affine holonomies.

Berger's list was later shown to be incomplete: further examples were found by R. Bryant (1991) and by Q. Chi, S. Merkulov, and L. Schwachhöfer (1996). These are sometimes known as exotic holonomies. The search for examples ultimately led to a complete classification of irreducible affine holonomies by Merkulov and Schwachhöfer (1999), with Bryant (2000) showing that every group on their list occurs as an affine holonomy group.

The Merkulov–Schwachhöfer classification has been clarified considerably by a connection between the groups on the list and certain symmetric spaces, namely the hermitian symmetric space

Hermitian symmetric space

In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian...

s and the quaternion-Kähler symmetric spaces. The relationship is particularly clear in the case of complex affine holonomies, as demonstrated by Schwachhöfer (2001).

Let V be a finite dimensional complex vector space, let H ⊂ Aut(V) be an irreducible semisimple complex connected Lie subgroup and let K ⊂ H be a maximal compact subgroup.

If there is an irreducible hermitian symmetric space of the form G/(U(1) · K), then both H and C^∗ · H are non-symmetric irreducible affine holonomy groups, where V the tangent representation of K.
If there is an irreducible quaternion-Kähler symmetric space of the form G/(Sp(1) · K), then H is a non-symmetric irreducible affine holonomy groups, as is C^∗ · H if dim V = 4. Here the complexified tangent representation of Sp(1) · K is C² ⊗ V, and H preserves a complex symplectic form on V.

These two families yield all non-symmetric irreducible complex affine holonomy groups apart from the following:

Using the classification of hermitian symmetric spaces, the first family gives the following complex affine holonomy groups:

where Z_C is either trivial, or the group C^*.

Using the classification of quaternion-Kähler symmetric spaces, the second family gives the following complex symplectic holonomy groups:

(In the second row, Z_C must be trivial unless n = 2.)

From these lists, an analogue of Simon's result that Riemannian holonomy groups act transitively on spheres may be observed: the complex holonomy representations are all prehomogeneous vector space

Prehomogeneous vector space

In mathematics, a prehomogeneous vector space is a finite-dimensional vector space V together with a subgroup G of GL such that G has an open dense orbit in V. Prehomogeneous vector spaces were introduced by Mikio Sato in 1970 and have many applications in geometry, number theory and analysis, as...

s. A conceptual proof of this fact is not known.

The classification of irreducible real affine holonomies can be obtained from a careful analysis, using the lists above and the fact that real affine holonomies complexify to complex ones.

Etymology

There's a similar word, "holomorphic

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

", that was introduced by two of Cauchy's students, Briot (1817–1882) and Bouquet (1819–1895), and derives from the Greek ὅλος (holos) meaning "entire", and μορφή (morphē) meaning "form" or "appearance".
The etymology of "holonomy" shares the first part with "holomorphic" (holos). About the second part:

See νόμος (nomos) and -nomy.

Holonomy of a connection in a vector bundle

Holonomy of a connection in a principal bundle

Holonomy bundles

Monodromy

Local and infinitesimal holonomy

Ambrose–Singer theorem

Riemannian holonomy

Reducible holonomy and the de Rham decomposition

The Berger classification

Special holonomy and spinors

Applications to string theory

Affine holonomy

Etymology

Further reading