
Jacobi field
Encyclopedia
In Riemannian geometry
, a Jacobi field is a vector field
along a geodesic
 in a Riemannian manifold
in a Riemannian manifold
describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space of all geodesics. They are named after Carl Jacobi.
one parameter family of geodesics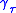 with
with 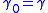 , then
, then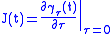
is a Jacobi field, and describes the behavior of the geodesics in an infinitesimal neighborhood of a
given geodesic .
.
A vector field J along a geodesic is said to be a Jacobi field if it satisfies the Jacobi equation:
is said to be a Jacobi field if it satisfies the Jacobi equation: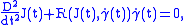
where D denotes the covariant derivative
with respect to the Levi-Civita connection
, R the Riemann curvature tensor
,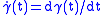 the tangent vector field, and t is the parameter of the geodesic.
the tangent vector field, and t is the parameter of the geodesic.
On a complete
Riemannian manifold, for any Jacobi field there is a family of geodesics describing the field (as in the preceding paragraph).
describing the field (as in the preceding paragraph).
The Jacobi equation is a linear
, second order ordinary
differential equation
;
in particular, values of and
and 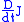 at one point of
at one point of  uniquely determine the Jacobi field. Furthermore, the set of Jacobi fields along a given geodesic forms a real vector space
uniquely determine the Jacobi field. Furthermore, the set of Jacobi fields along a given geodesic forms a real vector space
of dimension twice the dimension of the manifold.
As trivial examples of Jacobi fields one can consider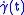 and
and 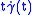 . These correspond respectively to the following families of reparametrisations:
. These correspond respectively to the following families of reparametrisations: 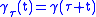 and
and 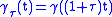 .
.
Any Jacobi field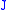 can be represented in a unique way as a sum
can be represented in a unique way as a sum  , where
, where 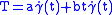 is a linear combination of trivial Jacobi fields and
is a linear combination of trivial Jacobi fields and 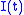 is orthogonal to
is orthogonal to 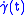 , for all
, for all  .
.
The field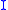 then corresponds to the same variation of geodesics as
then corresponds to the same variation of geodesics as 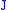 , only with changed parameterizations.
, only with changed parameterizations.
, the geodesic
s through the North pole are great circle
s. Consider two such geodesics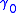 and
and 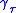 with natural parameter,
with natural parameter, 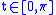 , separated by an angle
, separated by an angle  . The geodesic distance
. The geodesic distance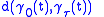
is
Computing this requires knowing the geodesics. The most interesting information is just that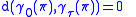 , for any
, for any  .
.
Instead, we can consider the derivative
with respect to at
at  :
: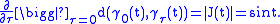
Notice that we still detect the intersection
of the geodesics at . Notice further that to calculate this derivative we do not actually need to know
. Notice further that to calculate this derivative we do not actually need to know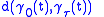 ,
,
rather, all we need do is solve the equation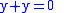 ,
,
for some given initial data.
Jacobi fields give a natural generalization of this phenomenon to arbitrary Riemannian manifold
s.
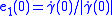 and complete this to get an orthonormal basis
and complete this to get an orthonormal basis  at
at 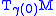 . Parallel transport
. Parallel transport
it to get a basis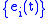 all along
all along  .
.
This gives an orthonormal basis with . The Jacobi field can be written in co-ordinates in terms of this basis as
. The Jacobi field can be written in co-ordinates in terms of this basis as 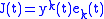 and thus
and thus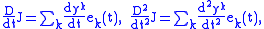
and the Jacobi equation can be rewritten as a system
for each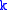 . This way we get a linear ordinary differential equation (ODE).
. This way we get a linear ordinary differential equation (ODE).
Since this ODE has smooth
coefficient
s we have that solutions exist for all and are unique, given
and are unique, given 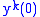 and
and 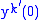 , for all
, for all 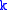 .
.
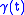 with parallel orthonormal frame
with parallel orthonormal frame 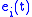 ,
, 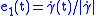 , constructed as above.
, constructed as above.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, a Jacobi field is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
along a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
 in a Riemannian manifold
in a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space of all geodesics. They are named after Carl Jacobi.
Definitions and properties
Jacobi fields can be obtained in the following way: Take a smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
one parameter family of geodesics
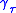 with
with 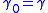 , then
, then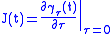
is a Jacobi field, and describes the behavior of the geodesics in an infinitesimal neighborhood of a
given geodesic
 .
.A vector field J along a geodesic
 is said to be a Jacobi field if it satisfies the Jacobi equation:
is said to be a Jacobi field if it satisfies the Jacobi equation: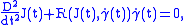
where D denotes the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
with respect to the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
, R the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
,
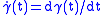 the tangent vector field, and t is the parameter of the geodesic.
the tangent vector field, and t is the parameter of the geodesic.On a complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
Riemannian manifold, for any Jacobi field there is a family of geodesics
 describing the field (as in the preceding paragraph).
describing the field (as in the preceding paragraph).The Jacobi equation is a linear
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
, second order ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
;
in particular, values of
 and
and 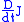 at one point of
at one point of  uniquely determine the Jacobi field. Furthermore, the set of Jacobi fields along a given geodesic forms a real vector space
uniquely determine the Jacobi field. Furthermore, the set of Jacobi fields along a given geodesic forms a real vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of dimension twice the dimension of the manifold.
As trivial examples of Jacobi fields one can consider
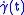 and
and 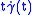 . These correspond respectively to the following families of reparametrisations:
. These correspond respectively to the following families of reparametrisations: 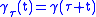 and
and 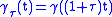 .
.Any Jacobi field
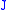 can be represented in a unique way as a sum
can be represented in a unique way as a sum  , where
, where 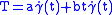 is a linear combination of trivial Jacobi fields and
is a linear combination of trivial Jacobi fields and 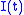 is orthogonal to
is orthogonal to 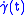 , for all
, for all  .
.The field
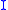 then corresponds to the same variation of geodesics as
then corresponds to the same variation of geodesics as 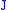 , only with changed parameterizations.
, only with changed parameterizations.Motivating example
On a sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s through the North pole are great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s. Consider two such geodesics
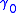 and
and 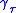 with natural parameter,
with natural parameter, 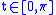 , separated by an angle
, separated by an angle  . The geodesic distance
. The geodesic distance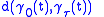
is

Computing this requires knowing the geodesics. The most interesting information is just that
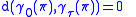 , for any
, for any  .
.Instead, we can consider the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
with respect to
 at
at  :
: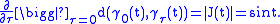
Notice that we still detect the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the geodesics at
 . Notice further that to calculate this derivative we do not actually need to know
. Notice further that to calculate this derivative we do not actually need to know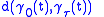 ,
,rather, all we need do is solve the equation
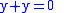 ,
,for some given initial data.
Jacobi fields give a natural generalization of this phenomenon to arbitrary Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s.
Solving the Jacobi equation
Let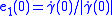 and complete this to get an orthonormal basis
and complete this to get an orthonormal basis  at
at 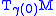 . Parallel transport
. Parallel transportParallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
it to get a basis
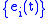 all along
all along  .
.This gives an orthonormal basis with
 . The Jacobi field can be written in co-ordinates in terms of this basis as
. The Jacobi field can be written in co-ordinates in terms of this basis as 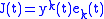 and thus
and thus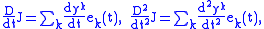
and the Jacobi equation can be rewritten as a system

for each
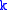 . This way we get a linear ordinary differential equation (ODE).
. This way we get a linear ordinary differential equation (ODE).Since this ODE has smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s we have that solutions exist for all
 and are unique, given
and are unique, given 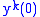 and
and 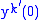 , for all
, for all 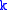 .
.Examples
Consider a geodesic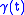 with parallel orthonormal frame
with parallel orthonormal frame 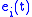 ,
, 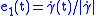 , constructed as above.
, constructed as above.
- The vector fields along
 given by
given by 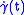 and
and 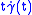 are Jacobi fields.
are Jacobi fields. - In Euclidean space (as well as for spaces of constant zero sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
) Jacobi fields are simply those fields linear in .
. - For Riemannian manifolds of constant negative sectional curvature
 , any Jacobi field is a linear combination of
, any Jacobi field is a linear combination of 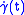 ,
, 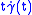 and
and 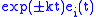 , where
, where  .
. - For Riemannian manifolds of constant positive sectional curvature
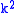 , any Jacobi field is a linear combination of
, any Jacobi field is a linear combination of 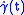 ,
, 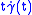 ,
, 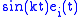 and
and 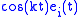 , where
, where  .
. - The restriction of a Killing vector fieldKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
to a geodesic is a Jacobi field in any Riemannian manifold. - The Jacobi fields correspond to the geodesics on the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
(with respect to the metric on induced by the metric on
induced by the metric on  ).
).
See also
- conjugate pointsConjugate pointsIn differential geometry, conjugate points are, roughly, points that can almost be joined by a 1-parameter family of geodesics. For example, on a sphere, the north-pole and south-pole are connected by any meridian.-Definition:...
- Geodesic deviation equationGeodesic deviation equationIn general relativity, the geodesic deviation equation is an equation involving the Riemann curvature tensor, which measures the change in separation of neighbouring geodesics or, equivalently, the tidal force experienced by a rigid body moving along a geodesic...
- Rauch comparison theoremRauch comparison theoremIn Riemannian geometry, the Rauch comparison theorem is a fundamental result which relates the sectional curvature of a Riemannian manifold to the rate at which geodesics spread apart. Intuitively, it states that for large curvature, geodesics tend to converge, while for small curvature,...
- N-Jacobi field

