
Principal curvature
Encyclopedia
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.
Discussion
At each point p of a differentiableDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
in 3-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
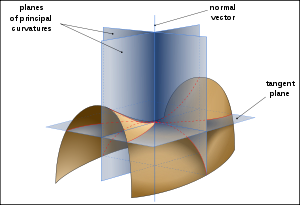
one may choose a unit normal vector. A normal plane at p is one that contains the normal, and will therefore also contain a unique direction tangent to the surface and cut the surface in a plane curve. This curve will in general have different curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
s for different normal planes at p. The principal curvatures at p, denoted k1 and k2, are the maximum and minimum values of this curvature.
Here the curvature of a curve is by definition the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
. The curvature is taken to be positive if the curve turns in the same direction as the surface's chosen normal, and otherwise negative. The directions of the normal plane where the curvature takes its maximum and minimum values are always perpendicular, a result of Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(1760), and are called principal directions. From a modern perspective, this theorem follows from the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
because they can be given as the principal axes of a symmetric tensor—the second fundamental form. A systematic analysis of the principal curvatures and principal directions was undertaken by Gaston Darboux, using Darboux frame
Darboux frame
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space...
s.
The product k1k2 of the two principal curvatures is the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, K, and the average (k1+k2)/2 is the mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, H.
If at least one of the principal curvatures is zero at every point, then the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
will be 0 and the surface is a developable surface
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...
. For a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
, the mean curvature is zero at every point.
Formal definition
Let M be a surface in Euclidean space with second fundamental form II(X,Y). Fix a point p∈M, and an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
X1, X2 of tangent vectors at p. Then the principal curvatures are the eigenvalues of the symmetric matrix

If X1 and X2 are selected so that the matrix [IIij] is a diagonal matrix, then they are called the principal directions. If the surface is oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, then one often requires that the pair (X1, X2) to be positively oriented with respect to the given orientation.
Without reference to a particular orthonormal basis, the principal curvatures are the eigenvalues of the shape operator, and the principal directions are its eigenvectors.
Generalizations
For hypersurfaces in higher dimensional Euclidean spaces, the principal curvatures may be defined in a directly analogous fashion. The principal curvatures are the eigenvalues of the matrix of the second fundamental form II(Xi,Xj) in an orthonormal basis of the tangent space. The principal directions are the corresponding eigenvectors.Similarly, if M is a hypersurface in a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
N, then the principal curvatures are the eigenvalues of its second-fundamental form. If k1, ..., kn are the n principal curvatures at a point p ∈ M and X1, ..., Xn are corresponding orthonormal eigenvectors (principal directions), then the sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
of M at p is given by

Classification of points on a surface
- At elliptical points, both principal curvatures have the same sign, and the surface is locally convex.
- At umbilic points, both principal curvatures are equal and every tangent vector can be considered a principal direction. These typically occur in isolated points.
- At hyperbolic points, the principal curvatures have opposite signs, and the surface will be locally saddle shaped.
- At parabolic points, one of the principal curvatures is zero. Parabolic points generally lie in a curve separating elliptical and hyperbolic regions.
- At flat umbilic points both principal curvatures are zero. A generic surface will not contain flat umbilic points. The Monkey saddleMonkey saddleIn mathematics, the monkey saddle is the surface defined by the equation z = x^3 - 3xy^2. \, It belongs to the class of saddle surfaces and its name derives from the observation that a saddle for a monkey requires three depressions: two for the legs, and one for the tail...
is one surface with an isolated flat umbilic.
- At flat umbilic points both principal curvatures are zero. A generic surface will not contain flat umbilic points. The Monkey saddle
Lines of curvature
The lines of curvature or curvature lines are curves which are always tangent to a principal direction (they are integral curveIntegral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s for the principal direction fields). There will be two lines of curvature through each non-umbilic point and the lines will cross at right angles.
In the vicinity of an umbilic the lines of curvature form one of three configurations star, lemon and monstar (derived from lemon-star). These points are also called Darbouxian Umbilics, in honor to
Gaston Darboux, the first to make a systematic study in Vol. 4, p455, of his Leçons (1896).
In these figures, the red curves are the lines of curvature for one family of principal directions, and the blue curves for the other.
When a line of curvature has a local extremum of the same principal curvature then the curve has a ridge point
Ridge (differential geometry)
For a smooth surface in three dimensions a ridge point occurs when a line of curvature has a local maximum or minimum of principal curvature. The set of ridge points form curves on the surface called ridges....
. These ridge points form curves on the surface called ridges. The ridge curves pass through the
umbilics. For the star pattern either 3 or 1 ridge line pass through the umbilic, for the monstar and lemon only one ridge passes through.

