Line (geometry)
Encyclopedia
The notion of line or straight line was introduced by the ancient mathematicians to represent straight
objects with negligible width and depth. Lines are an idealization of such objects. Thus, until seventeenth century, lines were defined like this: "The line is the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which [...] will leave from its imaginary moving some vestige in length, exempt of any width. [...] The straight line is that which is equally extended between its points"
Euclid
described a line as "breadthless length", and introduced several postulates as basic unprovable properties from which he constructed the geometry, which is now called Euclidean geometry
to avoid confusion with other geometries which have been introduced since the end of nineteenth century (such as non-Euclidean geometry
, projective geometry
, and affine geometry
).
In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry
, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation
, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.
When a geometry is described by a set of axiom
s, the notion of a line is usually left undefined (a so-called primitive
object). The properties of lines are then determined by the axioms which refer to them. One advantage to this approach is the flexibility it gives to users of the geometry. Thus in differential geometry a line may be interpreted as a geodesic
(shortest path between points), while in some projective geometries
a line is a 2-dimensional vector space (all linear combinations of two independent vectors). This flexibility also extends beyond mathematics and, for example, permits physicists to think of the path of a light ray as being a line.
A line segment
is a part of a line that is bounded by two distinct end points and contains every point on the line between its end points. Depending on how the line segment is defined, either of the two end points may or may not be part of the line segment. Two or more line segments may have some of the same relationships as lines, such as being parallel, intersecting, or skew.
in the Elements
, he defined lines to be "breadthless length" with a straight line being a line "which lies evenly with the points on itself". These definitions serve little purpose since they use terms which are not, themselves, defined. In fact, Euclid did not use these definitions in work and probably included them just to make it clear to the reader what was being discussed. In modern geometry, a line is simply taken as an undefined object with properties given by postulates, but is sometimes defined as a set of points obeying a linear relationship.http://webcache.googleusercontent.com/search?q=cache:N4keHx_oXY4J:www.ecs.syr.edu/faculty/fawcett/handouts/cse382/presentations/lvs.doc+line+%2Bset+of+points+%2Bhilbert+%2Bdefin&cd=1&ct=clnk&gl=uk
In an axiom
atic formulation of Euclidean geometry, such as that of Hilbert
(Euclid's original axioms contained various flaws which have been corrected by modern mathematicians), a line is stated to have certain properties which relate it to other lines and points
. For example, for any two distinct points, there is a unique line containing them, and any two distinct lines intersect in at most one point. In two dimension
s, i.e., the Euclidean plane
, two lines which do not intersect are called parallel
. In higher dimensions, two lines that do not intersect may be parallel if they are contained in a plane, or skew
if they are not.
Any collection of finitely many lines partitions the plane into convex polygon
s (possibly unbounded); this partition is known as an arrangement of lines
.
.svg.png)
In topology
, a ray in a space X is a continuous embedding R+ → X. It is used to define the important concept of end of the space.
s and linear function
s. In two dimensions, the characteristic equation is often given by the slope-intercept form: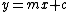
where:
The slope of the line through points A(ax, ay) and B(bx, by) is given by m = (by-ay)/(bx-ax)
and the equation of this line can be written y = m(x - ax) + ay.
In three dimensions, a line is described by parametric equations: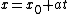
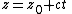
where:
In R2, every line L is described by a linear equation of the form
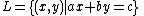
with fixed real coefficient
s a, b and c such that a and b are not both zero (see Linear equation
for other forms). Important properties of these lines are their slope, x-intercept and y-intercept.
The equation of the line passing through two different points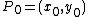
and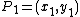 
may be written as
.
If x0 ≠ x1, this equation may be rewritten as
or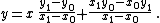
If a is vector OA and b is vector OB, then the equation of the line can be written: r = a + λ(b - a)
A ray starting at point A is described by limiting λ≥0
, this is the degenerate condition where three points do not determine a plane. The concept of collinearity is thus usually derived from a presumption of lines being in the geometry. However, in synthetic geometry
it has been known since 1900 that collinearity can be made a defined concept, and the notion of a line can be based upon it as a set of collinear points:
Consider the reflection
which swaps the points in a plane that are equal perpendicular distances from a given line L. The fixed point
s of the reflection are the points of L. Using d(u,v) to denote the distance between points u and v and selecting a pair of points a and b on L, note that if the reflection swaps x with y, then
The fixed point property of L can be expressed by saying that x and y are the same point: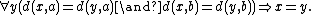
As expressed by Alessandro Padoa
at the International Congress of Mathematicians
(see page 357 of the Proceedings), x is collinear with a and b if there is no other point y which satisfies the congruences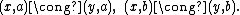
According to James T. Smith (2010)(American Mathematical Monthly
117:480), this characterization of collinearity was adapted from Gottfried Leibnitz.
Consequently, a line through points a and b in the Euclidean plane can be defined in terms of congruence
of point pairs as follows: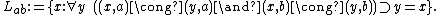
However, note that the notion of set formation is required in addition to the primitive notion
s of point and congruence.
In Giuseppe Peano
's geometry distance is taken as primitive and lines defined. The following formulation was given by Bertrand Russell
on page 410 of The Principles of Mathematics
:
To avoid the intricacies of set theory
, Alfred Tarski
has fashioned a Euclidean geometry without lines in his system of Tarski's axioms, content that the geometrical meaning of a line is sufficiently represented by logical collinearity.
In analytic geometry
, points A, B, and C are collinear if vector AB is parallel
to vector BC, or equivalently, if the slope
s of lines AB and AC are equal.
, Rn (and analogously in all other vector space
s), we define a line L as a subset of the form
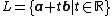
where a and b are given vectors in Rn with b non-zero. The vector b describes the direction of the line, and a is a point on the line. Different choices of a and b can yield the same line.
, a line is similar to that in Euclidean geometry but has slightly different properties. In many models of projective geometry, the idea of the line rarely conforms to the notion of the "straight curve" as it is visualised in Euclidean geometry. Elliptic geometry
is a typical example of when this happens.
s on differentiable manifold
s.
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
objects with negligible width and depth. Lines are an idealization of such objects. Thus, until seventeenth century, lines were defined like this: "The line is the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which [...] will leave from its imaginary moving some vestige in length, exempt of any width. [...] The straight line is that which is equally extended between its points"
Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
described a line as "breadthless length", and introduced several postulates as basic unprovable properties from which he constructed the geometry, which is now called Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
to avoid confusion with other geometries which have been introduced since the end of nineteenth century (such as non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, and affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
).
In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.
When a geometry is described by a set of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s, the notion of a line is usually left undefined (a so-called primitive
Primitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
object). The properties of lines are then determined by the axioms which refer to them. One advantage to this approach is the flexibility it gives to users of the geometry. Thus in differential geometry a line may be interpreted as a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
(shortest path between points), while in some projective geometries
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
a line is a 2-dimensional vector space (all linear combinations of two independent vectors). This flexibility also extends beyond mathematics and, for example, permits physicists to think of the path of a light ray as being a line.
A line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
is a part of a line that is bounded by two distinct end points and contains every point on the line between its end points. Depending on how the line segment is defined, either of the two end points may or may not be part of the line segment. Two or more line segments may have some of the same relationships as lines, such as being parallel, intersecting, or skew.
Euclidean geometry
When geometry was first formalised by EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
in the Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, he defined lines to be "breadthless length" with a straight line being a line "which lies evenly with the points on itself". These definitions serve little purpose since they use terms which are not, themselves, defined. In fact, Euclid did not use these definitions in work and probably included them just to make it clear to the reader what was being discussed. In modern geometry, a line is simply taken as an undefined object with properties given by postulates, but is sometimes defined as a set of points obeying a linear relationship.http://webcache.googleusercontent.com/search?q=cache:N4keHx_oXY4J:www.ecs.syr.edu/faculty/fawcett/handouts/cse382/presentations/lvs.doc+line+%2Bset+of+points+%2Bhilbert+%2Bdefin&cd=1&ct=clnk&gl=uk
In an axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic formulation of Euclidean geometry, such as that of Hilbert
Hilbert's axioms
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie , as the foundation for a modern treatment of Euclidean geometry...
(Euclid's original axioms contained various flaws which have been corrected by modern mathematicians), a line is stated to have certain properties which relate it to other lines and points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. For example, for any two distinct points, there is a unique line containing them, and any two distinct lines intersect in at most one point. In two dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s, i.e., the Euclidean plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, two lines which do not intersect are called parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
. In higher dimensions, two lines that do not intersect may be parallel if they are contained in a plane, or skew
Skew lines
In solid geometry, skew lines are two lines that do not intersect and are not parallel. Equivalently, they are lines that are not coplanar. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron...
if they are not.
Any collection of finitely many lines partitions the plane into convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
s (possibly unbounded); this partition is known as an arrangement of lines
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
.
Ray
If the concept of "order" of points of a line is defined, a ray, or half-line, may be defined as well. A ray is part of a line which is finite in one direction, but infinite in the other. It can be defined by two points, the initial point, A, and one other, B. The ray is all the points in the line segment between A and B together with all points, C, on the line through A and B such that the points appear on the line in the order A, B, C.Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a ray in a space X is a continuous embedding R+ → X. It is used to define the important concept of end of the space.
Coordinate geometry
In coordinate geometry, lines in a Cartesian plane can be described algebraically by linear equationLinear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s and linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
s. In two dimensions, the characteristic equation is often given by the slope-intercept form:
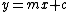
where:
- m is the slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
or gradientSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the line. - c is the y-interceptY-interceptIn coordinate geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept is a point where the graph of a function or relation intersects with the y-axis of the coordinate system...
of the line. - x is the independent variableIndependent variableThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
of the function y = f(x).
The slope of the line through points A(ax, ay) and B(bx, by) is given by m = (by-ay)/(bx-ax)
and the equation of this line can be written y = m(x - ax) + ay.
In three dimensions, a line is described by parametric equations:
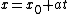
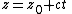
where:
- x, y, and z are all functions of the independent variable t.
- x0, y0, and z0 are the initial values of each respective variable (or (x0, y0, z0) is any point on the line).
- a, b, and c are related to the slope of the line, such that the vector (a, b, c) is a parallel to the line.
In R2, every line L is described by a linear equation of the form
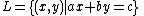
with fixed real coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s a, b and c such that a and b are not both zero (see Linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
for other forms). Important properties of these lines are their slope, x-intercept and y-intercept.
The equation of the line passing through two different points
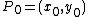and 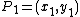may be written as.If x0 ≠ x1, this equation may be rewritten as
or
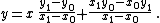
Vector equation
The vector equation of the line through points A and B is given by r = OA + λAB (where λ is a scalar multiple)If a is vector OA and b is vector OB, then the equation of the line can be written: r = a + λ(b - a)
A ray starting at point A is described by limiting λ≥0
Collinear points
Three points are said to be collinear if they lie on the same line. In the geometry of spaceSpace
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
, this is the degenerate condition where three points do not determine a plane. The concept of collinearity is thus usually derived from a presumption of lines being in the geometry. However, in synthetic geometry
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
it has been known since 1900 that collinearity can be made a defined concept, and the notion of a line can be based upon it as a set of collinear points:
Consider the reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
which swaps the points in a plane that are equal perpendicular distances from a given line L. The fixed point
Fixed point
"Fixed point" has many meanings in science, most of them mathematical.* Fixed point * Fixed-point combinator* Fixed-point arithmetic, a manner of doing arithmetic on computers* Benchmark , fixed points used by geodesists...
s of the reflection are the points of L. Using d(u,v) to denote the distance between points u and v and selecting a pair of points a and b on L, note that if the reflection swaps x with y, then
- d(x,a) = d(y,a) and d(x,b) = d(y,b).
The fixed point property of L can be expressed by saying that x and y are the same point:
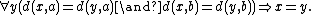
As expressed by Alessandro Padoa
Alessandro Padoa
Alessandro Padoa was an Italian mathematician and logician, a contributor to the school of Giuseppe Peano. He is remembered for a method for deciding whether, given some formal theory, a new primitive notion is truly independent of the other primitive notions...
at the International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
(see page 357 of the Proceedings), x is collinear with a and b if there is no other point y which satisfies the congruences
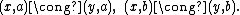
According to James T. Smith (2010)(American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
117:480), this characterization of collinearity was adapted from Gottfried Leibnitz.
Consequently, a line through points a and b in the Euclidean plane can be defined in terms of congruence
Congruence
Congruence is the state achieved by coming together, the state of agreement. The Latin congruō meaning “I meet together, I agree”. As an abstract term, congruence means similarity between objects...
of point pairs as follows:
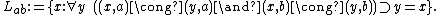
However, note that the notion of set formation is required in addition to the primitive notion
Primitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
s of point and congruence.
In Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
's geometry distance is taken as primitive and lines defined. The following formulation was given by Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
on page 410 of The Principles of Mathematics
The Principles of Mathematics
The Principles of Mathematics is a book written by Bertrand Russell in 1903. In it he presented his famous paradox and argued his thesis that mathematics and logic are identical....
:
- The straight line ab is the class of points x such that any point y, whose distances from a and b are respectively equal to the distances of x from a and b, must be coincident with x.
To avoid the intricacies of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
has fashioned a Euclidean geometry without lines in his system of Tarski's axioms, content that the geometrical meaning of a line is sufficiently represented by logical collinearity.
In analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, points A, B, and C are collinear if vector AB is parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to vector BC, or equivalently, if the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
s of lines AB and AC are equal.
Euclidean space
In Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, Rn (and analogously in all other vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s), we define a line L as a subset of the form
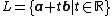
where a and b are given vectors in Rn with b non-zero. The vector b describes the direction of the line, and a is a point on the line. Different choices of a and b can yield the same line.
Projective geometry
In projective geometryProjective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, a line is similar to that in Euclidean geometry but has slightly different properties. In many models of projective geometry, the idea of the line rarely conforms to the notion of the "straight curve" as it is visualised in Euclidean geometry. Elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
is a typical example of when this happens.
Geodesics
The "straightness" of a line, interpreted as the property that it minimizes distances between its points, can be generalized and leads to the concept of geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s on differentiable manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s.
See also
- Real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
- Number lineNumber lineIn basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
- Line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
- Distance from a point to a lineDistance from a point to a lineThe distance from a point to a line is the shortest distance from a point to a line in Euclidean geometry. It can be calculated in the following ways.-Cartesian coordinates:...
- Plane (geometry), including Plane (geometry)#Distance from a point to a plane, which generalizes the distance from a point to a line.
- Affine function
- Five points determine a conicFive points determine a conicIn geometry, just as two points determine a line , five points determine a conic . There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.Formally, given any five points in the plane in general...
, just as two points determine a line - Glossary of Riemannian and metric geometry#R for its meaning in Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. - Incidence (geometry)Incidence (geometry)In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
- Plücker coordinatesPlücker coordinatesIn geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
- Minimal line representationRobotics conventionsThere are many conventions used in the robotics research field. This article summarises these conventions.-Line representations:Lines are very important in robotics because:...
- Ridge detectionRidge detectionThe ridges of a smooth function of two variables is a set of curves whose points are, in one or more ways to be made precise below, local maxima of the function in at least one dimension. For a function of N variables, its ridges are a set of curves whose points are local maxima in N-1 dimensions...
and Hough transformHough transformThe Hough transform is a feature extraction technique used in image analysis, computer vision, and digital image processing. The purpose of the technique is to find imperfect instances of objects within a certain class of shapes by a voting procedure...
for algorithms for detecting lines in digital images - Line drawing algorithmLine drawing algorithmA line drawing algorithm is a graphical algorithm for approximating a line segment on discrete graphical media. On discrete media, such as pixel-based displays and printers, line drawing requires such an approximation ....
External links
- Equations of the Straight Line at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Citizendium