
Coxeter-Dynkin diagram
Encyclopedia
In geometry
, a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph
with numerically labeled edges (called branches) representing the spatial relations between a collection of mirrors (or reflecting hyperplane
s). It describes a kaleidoscopic
construction: each graph node represents a mirror (domain facet
) and the label attached to a branch encodes the dihedral angle
order between two mirrors (on a domain ridge
). An unlabeled branch implicitly represents order-3.
Each diagram represents a Coxeter group
, and Coxeter groups are classified by their associated diagrams.
Dynkin diagrams are closely related objects, which differ from Coxeter diagrams in two respects: firstly, branches labeled "4" or greater are directed
, while Coxeter diagrams are undirected; secondly, Dynkin diagrams must satisfy an additional (crystallographic
) restriction, namely that the only allowed branch labels are 2, 3, 4, and 6. See Dynkin diagrams for details. Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras.
p, representing a dihedral angle
of 180°/p. When p = 2 the angle is 90 degrees and the mirrors have no interaction, so the branch can be omitted from the diagram. If a branch is unlabeled, it is assumed to have p = 3, representing an angle of 60 degrees. Two parallel mirrors have an branch marked with "∞". In principle, n mirrors can be represented by a complete graph
in which all n(n − 1)/2 branches are drawn. In practice, nearly all interesting configurations of mirrors include a number of right angles, so the corresponding branches are omitted.
within a given dimensional spherical or Euclidean or hyperbolic space. (In 2D spaces, a mirror is a line, and in 3D a mirror is a plane).
These visualizations show the fundamental domains for 2D and 3D Euclidean groups, and 2D spherical groups. For each the Coxeter diagram can be deduced by identifying the hyperplane mirrors and labelling their connectivity, ignoring 90 degree dihedral angles (order 2).
and uniform tessellation
s. Every uniform polytope with pure reflective symmetry (all but a few special cases have pure reflectional symmetry) can be represented by a Coxeter-Dynkin diagram with permutations of markups. Each uniform polytope can be generated using such mirrors and a single generator point: mirror images create new points as reflections, then polytope edges
can be defined between points and a mirror image point. Faces
can be constructed by cycles of edges created, etc. To specify the generating vertex, one or more nodes are marked with rings, meaning that the vertex is not on the mirror(s) represented by the ringed node(s). (If two or more mirrors are marked, the vertex is equidistant from them.) A mirror is active (creates reflections) only with respect to points not on it. A diagram needs at least one active node to represent a polytope.
All regular polytope
s, represented by Schläfli symbol symbol {p, q, r, ...}, can have their fundamental domain
s represented by a set of n mirrors with a related Coxeter–Dynkin diagram of a line of nodes and branches labeled by p, q, r, ..., with the first node ringed.
Uniform polytopes with one ring correspond to generator points at the corners of the fundamental domain simplex. Two rings correspond to the edges of simplex and have a degree of freedom, with only the midpoint as the uniform solution for equal edge lengths. In general k-rings generators are on k-faces of the simplex, and if all the nodes are ringed, the generator point is in the interior of the simplex.
A secondary markup convers a special case nonreflectional symmetry uniform polytopes. These cases exist as alternations of reflective symmetry polytopes. This mark up removes the central dot of a ringed node, called a hole (circles with nodes removed), to imply alternate nodes deleted. The resulting polytope will have a subsymmetry of the original Coxeter group
. If all the nodes are holes, the figure is considered a snub.
has a diagram: . This is also called octahedral symmetry
.
There are 7 convex uniform polyhedra
that can be constructed from this symmetry group and 3 from its alternation subsymmetries, each with a uniquely marked up Coxeter-Dynkin diagram. The Wythoff symbol
represents a special case of the Coxeter diagram for rank 3 graphs, with all 3 branch orders named, rather than suppressing the order 2 branches. The Wythoff symbol is able to handle the snub form, but not general alternations without all nodes ringed.
. All Coxeter group
Cartan matrices are symmetric because their root vectors are normalized. The Cartan matrix element ai,j = aj,i = -2*cos(π/p) where p is the branch order between the pairs of mirrors.
Rank 2 Coxeter diagrams and their corresponding Cartan matrices are given here. The Cartan matrices for higher rank groups can be as simply constructed with the matrix element pairs corresponding between each pair of mirrors.
The determinant
the Cartan matrix determines whether a group is finite (positive), affine (zero), or hyperbolic (negative). A hyperbolic group is compact if all subgroups are finite (i.e. have positive determinants).
symbols for the affine groups are given as also)
s. Hyperbolic groups are categorized as compact or not, with compact groups having bounded fundamental domains. Compact hyperbolic groups exist of rank 3 to 5, and noncompact groups exist up to rank 10.
s.
in the field of special
and general relativity
space-time, containing one (or more) time-like dimensional components whose self dot products are negative.
One usage includes the very-extended definitions which adds a third node to the over-extended simple groups. See family En (Lie algebra)
with E11 as a very-extended Coxeter-dynkin diagram.
A (simply-laced) Coxeter-Dynkin diagram (finite or affine) that has a symmetry (satisfying one condition, below) can be quotiented by the symmetry, yielding a new, generally multiply laced diagram, with the process called folding.
The one condition on the automorphism for folding to be possible is that distinct nodes of the graph in the same orbit (under the automorphism) must not be connected by an edge; at the level of root systems, roots in the same orbit must be orthogonal. At the level of diagrams, this is necessary as otherwise the quotient diagram will have a loop, due to identifying two nodes but having an edge between them, and loops are not allowed in Coxeter-Dynkin diagrams.
The nodes and edges of the quotient ("folded") diagram are the orbits of nodes and edges of the original diagram; the edges are single unless two incident edges map to the same edge (notably at nodes of valence greater than 2) – a "branch point" of the map, in which case the weight is the number of incident edges, and the arrow points towards the node at which they are incident – "the branch point maps to the non-homogeneous point".
For example, in D4 folding to G2, the edge in G2 points from the class of the 3 outer nodes (valence 1), to the class of the central node (valence 3).
Geometrically this corresponds to orthogonal projections of uniform polytope
s. Notably, any finite simply-laced Coxeter-Dynkin diagram can be folded to I2(h), where h is the Coxeter number
, which corresponds geometrically to a projection to the Coxeter plane.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with numerically labeled edges (called branches) representing the spatial relations between a collection of mirrors (or reflecting hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s). It describes a kaleidoscopic
Kaleidoscope
A kaleidoscope is a circle of mirrors containing loose, colored objects such as beads or pebbles and bits of glass. As the viewer looks into one end, light entering the other end creates a colorful pattern, due to the reflection off the mirrors...
construction: each graph node represents a mirror (domain facet
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
) and the label attached to a branch encodes the dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
order between two mirrors (on a domain ridge
Ridge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
). An unlabeled branch implicitly represents order-3.
Each diagram represents a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
, and Coxeter groups are classified by their associated diagrams.
Dynkin diagrams are closely related objects, which differ from Coxeter diagrams in two respects: firstly, branches labeled "4" or greater are directed
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, while Coxeter diagrams are undirected; secondly, Dynkin diagrams must satisfy an additional (crystallographic
Crystallographic restriction theorem
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...
) restriction, namely that the only allowed branch labels are 2, 3, 4, and 6. See Dynkin diagrams for details. Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras.
Description
Branches of a Coxeter–Dynkin diagram are labeled with a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
p, representing a dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
of 180°/p. When p = 2 the angle is 90 degrees and the mirrors have no interaction, so the branch can be omitted from the diagram. If a branch is unlabeled, it is assumed to have p = 3, representing an angle of 60 degrees. Two parallel mirrors have an branch marked with "∞". In principle, n mirrors can be represented by a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
in which all n(n − 1)/2 branches are drawn. In practice, nearly all interesting configurations of mirrors include a number of right angles, so the corresponding branches are omitted.
Geometric visualizations
The Coxeter-Dynkin diagram can be seen as a graphic description of the fundamental domain of mirrors. A mirror represents a hyperplaneHyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
within a given dimensional spherical or Euclidean or hyperbolic space. (In 2D spaces, a mirror is a line, and in 3D a mirror is a plane).
These visualizations show the fundamental domains for 2D and 3D Euclidean groups, and 2D spherical groups. For each the Coxeter diagram can be deduced by identifying the hyperplane mirrors and labelling their connectivity, ignoring 90 degree dihedral angles (order 2).
 Coxeter groups in the plane with equivalent diagrams. Domain mirrors are labeled as branch m1, m2, etc. Vertices are colored by their reflection order. The prismatic group  x x is shown as a doubling of the is shown as a doubling of the  , but can also be created as rectangular domains from doubling the , but can also be created as rectangular domains from doubling the  triangles. The triangles. The  is a doubling of the is a doubling of the 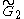 triangle. triangle. |
|
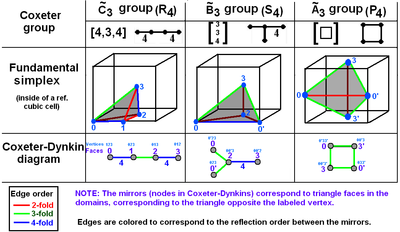 Coxeter groups in 3-space with diagrams. Mirrors (triangle faces) are labeled by opposite vertex 0..3. Branches are colored by their reflection order.  fills 1/48 of the cube. fills 1/48 of the cube.  fills 1/24 of the cube. fills 1/24 of the cube.  fills 1/12 of the cube. fills 1/12 of the cube. |
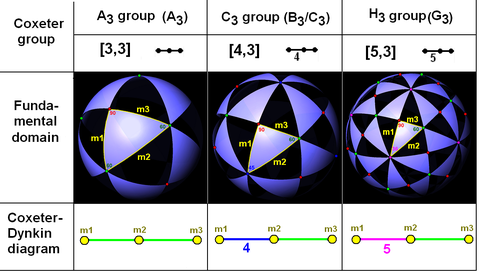 Coxeter groups in the sphere with equivalent diagrams. One fundamental domain is outlined in yellow. Domain vertices (and graph branches) are colored by their reflection order. |
Application with uniform polytopes
Coxeter–Dynkin diagrams can explicitly enumerate nearly all classes of uniform polytopeUniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
and uniform tessellation
Uniform tessellation
In geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
s. Every uniform polytope with pure reflective symmetry (all but a few special cases have pure reflectional symmetry) can be represented by a Coxeter-Dynkin diagram with permutations of markups. Each uniform polytope can be generated using such mirrors and a single generator point: mirror images create new points as reflections, then polytope edges
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
can be defined between points and a mirror image point. Faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
can be constructed by cycles of edges created, etc. To specify the generating vertex, one or more nodes are marked with rings, meaning that the vertex is not on the mirror(s) represented by the ringed node(s). (If two or more mirrors are marked, the vertex is equidistant from them.) A mirror is active (creates reflections) only with respect to points not on it. A diagram needs at least one active node to represent a polytope.
All regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s, represented by Schläfli symbol symbol {p, q, r, ...}, can have their fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
s represented by a set of n mirrors with a related Coxeter–Dynkin diagram of a line of nodes and branches labeled by p, q, r, ..., with the first node ringed.
Uniform polytopes with one ring correspond to generator points at the corners of the fundamental domain simplex. Two rings correspond to the edges of simplex and have a degree of freedom, with only the midpoint as the uniform solution for equal edge lengths. In general k-rings generators are on k-faces of the simplex, and if all the nodes are ringed, the generator point is in the interior of the simplex.
A secondary markup convers a special case nonreflectional symmetry uniform polytopes. These cases exist as alternations of reflective symmetry polytopes. This mark up removes the central dot of a ringed node, called a hole (circles with nodes removed), to imply alternate nodes deleted. The resulting polytope will have a subsymmetry of the original Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
. If all the nodes are holes, the figure is considered a snub.
- A single node represents a single mirror. This is called group A1. If ringed this creates a line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
perpendicular to the mirror, represented as {}. - Two unattached nodes represent two perpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
mirrors. If both nodes are ringed, a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
can be created, or a squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
if the point is at equal distance from both mirrors. - Two nodes attached by an order-n branch can create an n-gonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
if the point is on one mirror, and a 2n-gon if the point is off both mirrors. This forms the I1(n) group. - Two parallel mirrors can represent an infinite polygon I1(∞) group, also called I~1.
- Three mirrors in a triangle form images seen in a traditional kaleidoscopeKaleidoscopeA kaleidoscope is a circle of mirrors containing loose, colored objects such as beads or pebbles and bits of glass. As the viewer looks into one end, light entering the other end creates a colorful pattern, due to the reflection off the mirrors...
and can be represented by three nodes connected in a triangle. Repeating examples will have branches labeled as (3 3 3), (2 4 4), (2 3 6), although the last two can be drawn as a line (with the 2 branches ignored). These will generate uniform tilingsTiling by regular polygonsPlane tilings by regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in Harmonices Mundi.- Regular tilings :...
. - Three mirrors can generate uniform polyhedra; including rational numbers gives the set of Schwarz triangleSchwarz triangleIn geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s. - Three mirrors with one perpendicular to the other two can form the uniform prismsPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
.
Example BC3 polytopes
For example, the BC3 Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
has a diagram: . This is also called octahedral symmetry
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
.
There are 7 convex uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
that can be constructed from this symmetry group and 3 from its alternation subsymmetries, each with a uniquely marked up Coxeter-Dynkin diagram. The Wythoff symbol
Wythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
represents a special case of the Coxeter diagram for rank 3 graphs, with all 3 branch orders named, rather than suppressing the order 2 branches. The Wythoff symbol is able to handle the snub form, but not general alternations without all nodes ringed.
| Name | Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
Truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
Rhombi-cuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
Truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
Snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
|---|---|---|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Coxeter diagram |
||||||||||
| Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.... |
3 | 2 4 | 3 2 | 4 | 2 | 4 3 | 4 2 | 3 | 4 | 2 3 | 4 3 | 2 | 4 3 2 | | | 4 3 2 | ||
| Symmetry group | Oh | O | Td | Th | ||||||
| *432 | 432 | *332 | 3*2 | |||||||
| [4,3] | [4,3]+ | [1+,4,3] =[3,3] | [4,3+] | |||||||
Cartan Matrices
Every Coxeter diagram has a corresponding Cartan matrixCartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
. All Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
Cartan matrices are symmetric because their root vectors are normalized. The Cartan matrix element ai,j = aj,i = -2*cos(π/p) where p is the branch order between the pairs of mirrors.
Rank 2 Coxeter diagrams and their corresponding Cartan matrices are given here. The Cartan matrices for higher rank groups can be as simply constructed with the matrix element pairs corresponding between each pair of mirrors.
The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
the Cartan matrix determines whether a group is finite (positive), affine (zero), or hyperbolic (negative). A hyperbolic group is compact if all subgroups are finite (i.e. have positive determinants).
| Symmetry order p |
Group name |
Coxeter diagram | Cartan matrix | |||
|---|---|---|---|---|---|---|
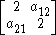 |
Determinant (4-a21*a12) |
|||||
| Finite (Determinant>0) | ||||||
| 2 | I2(2) = A1xA1 | 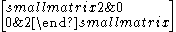 |
4 | |||
| 3 | I2(3) = A2 | 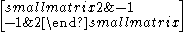 |
3 | |||
| 4 | I2(4) = BC2 | 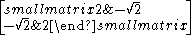 |
2 | |||
| 5 | I2(5) = H2 |  |
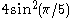
|
|||
| 6 | I2(6) = G2 | 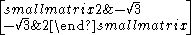 |
1 | |||
| 8 | I2(8) |  |
 ~0.58578643763 |
|||
| 10 | I2(10) |  |

|
|||
| 12 | I2(12) | 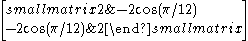 |
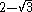 ~0.26794919243 |
|||
| p | I2(p) |  |
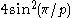 |
|||
| Affine (Determinant=0) | ||||||
| ∞ | I2(∞) = 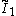 = = 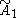 |
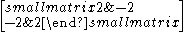 |
0 | |||
Finite Coxeter groups
- See also :polytope families for a table of end-node uniform polytopes associated with these groups.
- Three different symbols are given for the same groups – as a letter/number, as a bracketed set of numbers, and as the Coxeter diagram.
- The bifurcated Dn groups is half or alternated version of the regular Cn groups.
- The bifurcated Dn and En groups are also labeled by a superscript form [3a,b,c] where a,b,c are the numbers of segments in each of the three branches.
| Rank | Simple Lie group Simple Lie group In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself... s |
Exceptional Lie groups | |||||
|---|---|---|---|---|---|---|---|
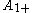 |
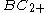 |
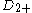 |
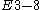 En (Lie algebra) In mathematics, especially in Lie theory, En is the Kac–Moody algebra whose Dynkin diagram is a bifurcating graph with three branches of length 1,2, and k, with k=n-4.... |
 / / 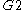 |
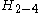 |
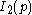 |
|
| 1 | A1=[] | ||||||
| 2 | A2=[3] | BC2=[4] | D2=A1xA1 | G2=[6] | H2=[6] | I2[p] | |
| 3 | A3=[32] | BC3=[3,4] | D3=A3 | E3=A2xA1
|
H3 | ||
| 4 | A4=[33] | BC4=[32,4] | D4=[31,1,1] | E4=A4 | F4 | H4 | |
| 5 | A5=[34] | BC5=[33,4] | D5=[32,1,1] | E5=D5 | |||
| 6 | A6=[35] | BC6=[34,4] | D6=[33,1,1] | E6=[32,2,1] | |||
| 7 | A7=[36] | BC7=[35,4] | D7=[34,1,1] | E7=[33,2,1] | |||
| 8 | A8=[37] | BC8=[36,4] | D8=[35,1,1] | E8=[34,2,1] | |||
| 9 | A9=[38] | BC9=[37,4] | D9=[36,1,1] | ||||
| 10+ | .. | .. | .. | .. | |||
Affine Coxeter groups
Families of convex uniform Euclidean tessellations are defined by the affine Coxeter groups. These groups are identical to the finite groups with the inclusion of one added node. In letter names they are given the same letter with a "~" above the letter. The index refers to the finite group, so the rank is the index plus 1. (Ernst WittErnst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
symbols for the affine groups are given as also)
 : diagrams of this type are cycles. (Also Pn)
: diagrams of this type are cycles. (Also Pn)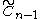 is associated with the hypercube regular tessellation family {4,3,....,4} family. (Also Rn)
is associated with the hypercube regular tessellation family {4,3,....,4} family. (Also Rn)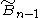 related to C by one removed mirror. (Also Sn)
related to C by one removed mirror. (Also Sn)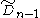 related to C by two removed mirror. (Also Qn)
related to C by two removed mirror. (Also Qn) ,
, 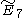 ,
, 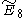 . (Also T7, T8, T9)
. (Also T7, T8, T9)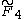 forms the {3,4,3,3} regular tessellation. (Also U5)
forms the {3,4,3,3} regular tessellation. (Also U5)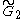 forms 30-60-90 triangle fundamental domains. (Also V3)
forms 30-60-90 triangle fundamental domains. (Also V3)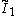 is two parallel mirrors. ( =
is two parallel mirrors. ( =  =
= 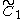 ) (Also W2)
) (Also W2)
| Rank | 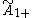 (P2+) (P2+) |
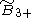 (S4+) (S4+) |
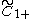 (R2+) (R2+) |
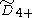 (Q5+) (Q5+) |
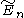 (Tn+1) / (Tn+1) / 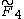 (U5) / (U5) / 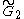 (V3) (V3) |
|---|---|---|---|---|---|
| 2 | 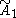 =[∞] =[∞] |
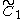 =[∞] =[∞] |
|||
| 3 | 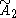 =[3[3]] =[3[3]] |
 =[4,4] =[4,4] |
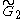 =[6,3] =[6,3] |
||
| 4 | 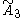 =[3[4]] =[3[4]] |
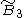 =[4,31,1] =[4,31,1] |
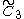 =[4,3,4] =[4,3,4] |
||
| 5 | 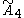 =[3[5]] =[3[5]] |
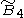 =[4,3,31,1] =[4,3,31,1] |
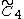 =[4,32,4] =[4,32,4] |
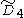 =[31,1,1,1] =[31,1,1,1] |
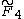 =[3,4,3,3] =[3,4,3,3] |
| 6 | 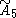 =[3[6]] =[3[6]] |
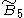 =[4,32,31,1] =[4,32,31,1] |
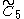 =[4,33,4] =[4,33,4] |
 =[31,1,3,31,1] =[31,1,3,31,1] |
|
| 7 | 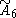 =[3[7]] =[3[7]] |
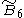 =[4,33,31,1] =[4,33,31,1] |
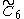 =[4,34,4] =[4,34,4] |
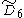 =[31,1,32,31,1] =[31,1,32,31,1] |
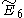 =[32,2,2] =[32,2,2] |
| 8 |  =[3[8]] =[3[8]] |
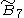 =[4,34,31,1] =[4,34,31,1] |
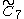 =[4,35,4] =[4,35,4] |
 =[31,1,33,31,1] =[31,1,33,31,1] |
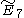 =[33,3,1] =[33,3,1] |
| 9 | 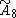 =[3[9]] =[3[9]] |
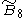 =[4,35,31,1] =[4,35,31,1] |
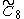 =[4,36,4] =[4,36,4] |
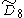 =[31,1,34,31,1] =[31,1,34,31,1] |
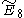 =[35,2,1] =[35,2,1] |
| 10 | 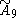 =[3[10]] =[3[10]] |
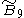 =[4,36,31,1] =[4,36,31,1] |
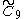 =[4,37,4] =[4,37,4] |
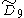 =[31,1,35,31,1] =[31,1,35,31,1] |
|
| 11 | ... | ... | ... | ... |
Hyperbolic Coxeter groups
There are many infinite hyperbolic Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s. Hyperbolic groups are categorized as compact or not, with compact groups having bounded fundamental domains. Compact hyperbolic groups exist of rank 3 to 5, and noncompact groups exist up to rank 10.
Rank 3
There are infinitely many compact hyperbolic Coxeter groups of rank 3, including linear and triangle graphs. See notably the hyperbolic triangle groupTriangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
s.
| Linear | Cyclic | ||||
|---|---|---|---|---|---|
| ∞: [p,q], 2(p+q) ... ... ... |
∞ [(p,q,r)], p+q+r>9
|
Ranks 4 to 5
The fundamental domain of either of the two bifurcating groups, [5,31,1] and [5,3,31,1], is double that of a corresponding linear group, [5,3,4] and [5,3,3,4] respectively.| Dimension Hd |
Rank | Total count | Linear | Bifurcating | Cyclic |
|---|---|---|---|---|---|
| H3 | 4 | 9 | 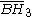 = [4,3,5]: = [4,3,5]: 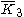 = [5,3,5]: = [5,3,5]: 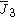 = [3,5,3]: = [3,5,3]: |
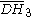 = [5,31,1]: = [5,31,1]: |
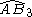 = [(3,3,3,4)]: = [(3,3,3,4)]: 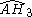 = [(3,3,3,5)]: = [(3,3,3,5)]:  = [(3,4,3,4)]: = [(3,4,3,4)]: 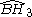 = [(3,4,3,5)]: = [(3,4,3,5)]: 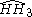 = [(3,5,3,5)]: = [(3,5,3,5)]: |
| H4 | 5 | 5 | 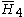 = [3,3,3,5]: = [3,3,3,5]: 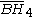 = [4,3,3,5]: = [4,3,3,5]: 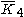 = [5,3,3,5]: = [5,3,3,5]: |
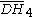 = [5,3,31,1]: = [5,3,31,1]: |
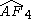 = [(3,3,3,3,4)]: = [(3,3,3,3,4)]: |
Rank 3
Noncompact Coxeter groups of rank 3 include linear and triangle graphs with one or more infinite order branches: (p and q = 3,4,5...)| Linear graphs | Cyclic graphs |
|---|---|
|
|
Ranks 4 to 10
There are a total of 58 noncompact hyperbolic Coxeter groups from rank 4 through 10. All 58 are grouped below in five categories. Letter symbols are given by Johnson as Extended Witt symbols, using PQRSTWUV from the affine Witt symbols, and adding LMNOXYZ. These hyperbolic groups are given an overline, or a hat, for purely cyclic graphs. The bracket notation from Coxeter is a linearized representation of the Coxeter group.| Rank | Total count |
Groups | |||
|---|---|---|---|---|---|
| 4 | 23 | 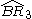 = [(3,3,4,4)]: = [(3,3,4,4)]: 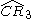 = [(3,4,4,4)]: = [(3,4,4,4)]: 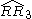 = [(4,4,4,4)]: = [(4,4,4,4)]:  = [(3,3,3,6)]: = [(3,3,3,6)]: 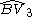 = [(3,4,3,6)]: = [(3,4,3,6)]: 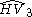 = [(3,5,3,6)]: = [(3,5,3,6)]:  = [(3,6,3,6)]: = [(3,6,3,6)]: |
 = [3,3[3]]: = [3,3[3]]: 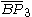 = [4,3[3]]: = [4,3[3]]: 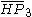 = [5,3[3]]: = [5,3[3]]: 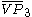 = [6,3[3]]: = [6,3[3]]: 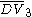 = [6,31,1]: = [6,31,1]: 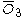 = [6,41,1]: = [6,41,1]: 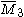 = [4,41,1]: = [4,41,1]: |
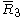 = [3,4,4]: = [3,4,4]: 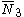 = [4,4,4]: = [4,4,4]: 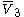 = [3,3,6]: = [3,3,6]: 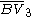 = [4,3,6]: = [4,3,6]: 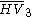 = [5,3,6]: = [5,3,6]: 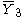 = [3,6,3]: = [3,6,3]: 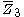 = [6,3,6]: = [6,3,6]: |
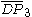 = [3[ ]x[ ]]: = [3[ ]x[ ]]: 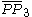 = [3[3,3]]: = [3[3,3]]: |
| 5 | 9 | 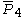 = [3,3[4]]: = [3,3[4]]:
|
 = [4,/3\,3,4]: = [4,/3\,3,4]: 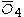 = [3,4,31,1]: = [3,4,31,1]: 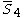 = [4,32,1]: = [4,32,1]: |
 = [3,4,3,4]: = [3,4,3,4]: |
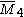 = [4,31,1,1]: = [4,31,1,1]: |
| 6 | 12 | 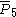 = [3,3[5]]: = [3,3[5]]: 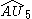 = [(3,3,3,3,3,4)]: = [(3,3,3,3,3,4)]:
|
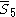 = [4,3,32,1]: = [4,3,32,1]: 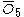 = [3,4,31,1]: = [3,4,31,1]: 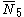 = [4,3,/3\,3,4]: = [4,3,/3\,3,4]: |
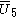 = [3,3,3,4,3]: = [3,3,3,4,3]: 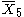 = [3,3,4,3,3]: = [3,3,4,3,3]: 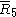 = [3,4,3,3,4]: = [3,4,3,3,4]: |
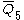 = [32,1,1,1]: = [32,1,1,1]:  = [4,3,31,1,1]: = [4,3,31,1,1]:  = [31,1,1,1,1]: = [31,1,1,1,1]: |
| 7 | 3 | 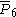 = [3,3[6]]: = [3,3[6]]: |
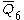 = [31,1,3,32,1]: = [31,1,3,32,1]: |
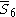 = [4,3,3,32,1]: = [4,3,3,32,1]: |
|
| 8 | 4 | 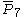 = [3,3[7]]: = [3,3[7]]: |
 = [31,1,32,32,1]: = [31,1,32,32,1]: |
 = [4,33,32,1]: = [4,33,32,1]: |
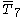 = [33,2,2]: = [33,2,2]: |
| 9 | 4 | 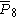 = [3,3[8]]: = [3,3[8]]: |
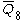 = [31,1,33,32,1]: = [31,1,33,32,1]: |
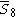 = [4,34,32,1]: = [4,34,32,1]: |
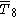 = [34,3,1]: = [34,3,1]: |
| 10 | 3 | 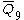 = [31,1,34,32,1]: = [31,1,34,32,1]: |
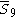 = [4,35,32,1]: = [4,35,32,1]: |
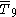 = [36,2,1]: = [36,2,1]: |
|
Beyond hyperbolic groups
Coxeter groups can be defined as graphs beyond the hyperbolic forms. These can be considered to be related to a Lorentzian geometry, named after Hendrik LorentzHendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
in the field of special
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
space-time, containing one (or more) time-like dimensional components whose self dot products are negative.
One usage includes the very-extended definitions which adds a third node to the over-extended simple groups. See family En (Lie algebra)
En (Lie algebra)
In mathematics, especially in Lie theory, En is the Kac–Moody algebra whose Dynkin diagram is a bifurcating graph with three branches of length 1,2, and k, with k=n-4....
with E11 as a very-extended Coxeter-dynkin diagram.
Geometric folding
Finite |
Affine |
Hyperbolic |
A (simply-laced) Coxeter-Dynkin diagram (finite or affine) that has a symmetry (satisfying one condition, below) can be quotiented by the symmetry, yielding a new, generally multiply laced diagram, with the process called folding.
The one condition on the automorphism for folding to be possible is that distinct nodes of the graph in the same orbit (under the automorphism) must not be connected by an edge; at the level of root systems, roots in the same orbit must be orthogonal. At the level of diagrams, this is necessary as otherwise the quotient diagram will have a loop, due to identifying two nodes but having an edge between them, and loops are not allowed in Coxeter-Dynkin diagrams.
The nodes and edges of the quotient ("folded") diagram are the orbits of nodes and edges of the original diagram; the edges are single unless two incident edges map to the same edge (notably at nodes of valence greater than 2) – a "branch point" of the map, in which case the weight is the number of incident edges, and the arrow points towards the node at which they are incident – "the branch point maps to the non-homogeneous point".
For example, in D4 folding to G2, the edge in G2 points from the class of the 3 outer nodes (valence 1), to the class of the central node (valence 3).
Geometrically this corresponds to orthogonal projections of uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s. Notably, any finite simply-laced Coxeter-Dynkin diagram can be folded to I2(h), where h is the Coxeter number
Coxeter number
In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group, hence also of a root system or its Weyl group. It is named after H.S.M. Coxeter.-Definitions:...
, which corresponds geometrically to a projection to the Coxeter plane.
See also
- Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
- Dynkin diagram
- Uniform polytopeUniform polytopeA uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
- Wythoff symbolWythoff symbolIn geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
- Uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
- List of uniform polyhedra
- List of uniform planar tilings
- Uniform polychoronUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
- Convex uniform honeycombConvex uniform honeycombIn geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
- Convex uniform honeycombs in hyperbolic spaceConvex uniform honeycombs in hyperbolic spaceIn geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by ring permutations of the Coxeter–Dynkin...
- Wythoff symbol
- Wythoff constructionWythoff constructionIn geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
and Wythoff symbolWythoff symbolIn geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
External links
- October 1978 discussion on the history of the Coxeter diagrams by Coxeter and Dynkin in TorontoTorontoToronto is the provincial capital of Ontario and the largest city in Canada. It is located in Southern Ontario on the northwestern shore of Lake Ontario. A relatively modern city, Toronto's history dates back to the late-18th century, when its land was first purchased by the British monarchy from...
, CanadaCanadaCanada is a North American country consisting of ten provinces and three territories. Located in the northern part of the continent, it extends from the Atlantic Ocean in the east to the Pacific Ocean in the west, and northward into the Arctic Ocean...
; Eugene Dynkin Collection of Mathematics Interviews, Cornell University LibraryCornell University LibraryThe Cornell University Library is the library system of Cornell University. In 2010 it held 8 million printed volumes in open stacks, 8.5 million microfilms and microfiches, more than of manuscripts, and close to 500,000 other materials, including motion pictures, DVDs, sound recordings, and...
.



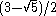
 = [4,3[4]]:
= [4,3[4]]: 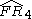 = [(3,3,4,3,4)]:
= [(3,3,4,3,4)]: 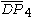 = [3[3]x[ ]]:
= [3[3]x[ ]]: 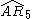 = [(3,3,4,3,3,4)]:
= [(3,3,4,3,3,4)]: