.gif)
F4 (mathematics)
Encyclopedia
In mathematics
, F4 is the name of a Lie group
and also its Lie algebra
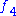. It is one of the five exceptional simple Lie group
s. F4 has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group
is the trivial group
. Its fundamental representation
is 26-dimensional.
The compact real form of F4 is the isometry group
of a 16-dimensional Riemannian manifold
known as the 'octonionic projective plane', OP2. This can be seen systematically using a construction known as the magic square
, due to Hans Freudenthal
and Jacques Tits
.
There are 3 real forms: a compact one, a split one, and a third one.
The F4 Lie algebra may be constructed by adding 16 generators transforming as a spinor
to the 36-dimensional Lie algebra so(9), in analogy with the construction of E8
.
In older books and papers, F4 is sometimes denoted by E4.
/Coxeter
group is the symmetry group
of the 24-cell: it is a solvable group
of order 1152.
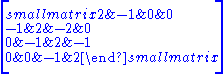
is a four dimensional body-centered cubic lattice (i.e. the union of two hypercubic lattices, each lying in the center of the other). They form a ring
called the Hurwitz quaternion
ring. The 24 Hurwitz quaternions of norm 1 form the 24-cell.
24-cell vertices:
Dual 24-cell vertices:
s for F4 is given by the rows of the following matrix: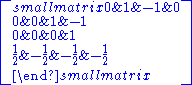
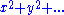invariant, 
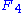is the group of automorphisms of the following set of 3 polynomials in 27 variables. (The first can easily be substituted into other two making 26 variables).
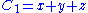
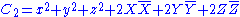
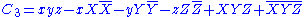
Where x,y,z are real valued and X,Y,Z are octonion valued. Another way of writing these invariants is as (combinations of)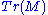
, 
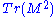and 
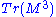of the hermitian octonion
matrix
:
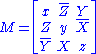
is the only exceptional lie group which gives the automorphisms of a set of real commutative polynomials. (The other exceptional lie groups require anti-commutative polynomial invariants).
. The dimensions of the smallest irreducible representations are :
The 52-dimensional representation is the adjoint representation, and the 26-dimensional one is the trace-free part of the action of F4 on the exceptional Albert algebra
of dimension 27.
There are two non-isomorphic irreducible representations of dimensions 1053, 160056, 4313088, etc. The fundamental representation
s are those with dimensions 52, 1274, 273, 26 (corresponding to the four nodes in the Dynkin diagram in the order such that the double arrow points from the second to the third).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, F4 is the name of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and also its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
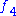. It is one of the five exceptional simple Lie groupSimple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s. F4 has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
. Its fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
is 26-dimensional.
The compact real form of F4 is the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of a 16-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
known as the 'octonionic projective plane', OP2. This can be seen systematically using a construction known as the magic square
Freudenthal magic square
In mathematics, the Freudenthal magic square is a construction relating several Lie groups. It is named after Hans Freudenthal and Jacques Tits, who developed the idea independently. It associates a Lie group to a pair of division algebras A, B...
, due to Hans Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
and Jacques Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
.
There are 3 real forms: a compact one, a split one, and a third one.
The F4 Lie algebra may be constructed by adding 16 generators transforming as a spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
to the 36-dimensional Lie algebra so(9), in analogy with the construction of E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
.
In older books and papers, F4 is sometimes denoted by E4.
Weyl/Coxeter group
Its WeylWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
/Coxeter
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
group is the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the 24-cell: it is a solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
of order 1152.
Cartan matrix
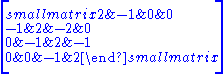
F4 lattice
The F4 latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
is a four dimensional body-centered cubic lattice (i.e. the union of two hypercubic lattices, each lying in the center of the other). They form a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
called the Hurwitz quaternion
Hurwitz quaternion
In mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
ring. The 24 Hurwitz quaternions of norm 1 form the 24-cell.
Roots of F4
The 48 root vectors of F4 can be found as the vertices of the 24-cell in two dual configurations:24-cell vertices:
- 24 roots by (±1,±1,0,0), permutating coordinate positions
Dual 24-cell vertices:
- 8 roots by (±1, 0, 0, 0), permutating coordinate positions
- 16 roots by (±½, ±½, ±½, ±½).
Simple roots
One choice of simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s for F4 is given by the rows of the following matrix:
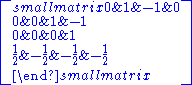
F4 polynomial invariant
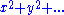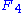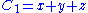
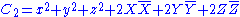
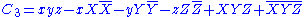
Just as O(n) is the group of automorphisms which keep the quadratic polymials invariant, is the group of automorphisms of the following set of 3 polynomials in 27 variables. (The first can easily be substituted into other two making 26 variables).Where x,y,z are real valued and X,Y,Z are octonion valued. Another way of writing these invariants is as (combinations of)
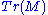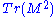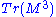, and of the hermitian octonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
:
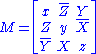
is the only exceptional lie group which gives the automorphisms of a set of real commutative polynomials. (The other exceptional lie groups require anti-commutative polynomial invariants).Representations
The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formulaWeyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
. The dimensions of the smallest irreducible representations are :
- 1, 26, 52, 273, 324, 1053 (twice), 1274, 2652, 4096, 8424, 10829, 12376, 16302, 17901, 19278, 19448, 29172, 34749, 76076, 81081, 100776, 106496, 107406, 119119, 160056 (twice), 184756, 205751, 212992, 226746, 340119, 342056, 379848, 412776, 420147, 627912…
The 52-dimensional representation is the adjoint representation, and the 26-dimensional one is the trace-free part of the action of F4 on the exceptional Albert algebra
Albert algebra
In mathematics, an Albert algebra is a 27-dimensional exceptional Jordan algebra. They are named after Abraham Adrian Albert, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to isomorphism...
of dimension 27.
There are two non-isomorphic irreducible representations of dimensions 1053, 160056, 4313088, etc. The fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
s are those with dimensions 52, 1274, 273, 26 (corresponding to the four nodes in the Dynkin diagram in the order such that the double arrow points from the second to the third).