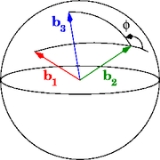
Dihedral angle
Overview
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a dihedral or torsion angle is the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
between two plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
s.
The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection. The dihedral angle
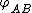 between two planes denoted A and B is the angle
between two planes denoted A and B is the anglebetween their two normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
unit vectors
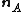 and
and 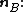

A dihedral angle can be signed
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
; for example, the dihedral angle
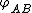 can be defined as the angle through which plane A must be rotated (about their common line of intersection) to align it with plane B.
can be defined as the angle through which plane A must be rotated (about their common line of intersection) to align it with plane B.Thus,
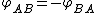 .
.
Unanswered Questions

