
Hyperplane
Encyclopedia
A hyperplane is a concept in geometry
. It is a generalization of the plane into a different number of dimensions.
A hyperplane of an n-dimensional space is a flat
subset with dimension n − 1. By its nature, it separates the space into two half spaces.
, a hyperplane of an n-dimensional space V is a "flat" subset of dimension n − 1, or equivalently, of codimension
1 in V; it may therefore be referred to as an (n − 1)-flat
of V. The space V may be a Euclidean space
or more generally an affine space
, or a vector space
or a projective space
, and the notion of hyperplane varies correspondingly; in all cases however, any hyperplane can be given in coordinates as the solution of a single (due to the "codimension 1" constraint) algebraic equation of degree 1 (due to the "flat" constraint). If V is a vector space, one distinguishes "vector hyperplanes" (which are subspaces, and therefore must pass through the origin) and "affine hyperplanes" (which need not pass through the origin; they can be obtained by translation
of a vector hyperplane). A hyperplane in a Euclidean space separates that space into two half spaces, and defines a reflection
that fixes the hyperplane and interchanges those two half spaces.
between two non-parallel hyperplanes of a Euclidean space is the angle between the corresponding normal vectors. The product of the reflections in the two hyperplanes is a rotation
whose axis is the subspace of codimension 2 obtained by intersecting the hyperplanes, and whose angle is twice the angle between the hyperplanes.
of codimension
1 in an affine space
.
In Cartesian coordinates, such a hyperplane can be described with a single linear equation
of the following form (where at least one of the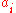 's is non-zero):
's is non-zero):

In the case of a real affine space, in other words when the coordinates are real numbers, this affine space separates the space into two half-spaces, which are the connected components of the complement
of the hyperplane, and are given by the inequalities
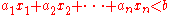
and

As an example, a line is a hyperplane in 2-dimensional space, and a plane is a hyperplane in 3-dimensional space. A line in 3-dimensional space is not a hyperplane, and does not separate the space into two parts (the complement of such a line is connected).
Any hyperplane of a Euclidean space has exactly two unit normal vectors.
Affine hyperplanes are used to define decision boundaries in many machine learning
algorithms such as linear-combination (oblique) decision trees
, and Perceptron
s.
s (points at infinity) added. An affine hyperplane together with the associated points at infinity forms a projective hyperplane. One special case of a projective hyperplane is the infinite or ideal hyperplane, which is defined with the set of all points at infinity.
In real projective space, a hyperplane does not divide the space into two parts; rather, it takes two hyperplanes to separate points and divide up the space. The reason for this is that in real projective space, the space essentially "wraps around" so that both sides of a lone hyperplane are connected to each other.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. It is a generalization of the plane into a different number of dimensions.
A hyperplane of an n-dimensional space is a flat
Flat (geometry)
In geometry, a flat is a subset of n-dimensional space that is congruent to a Euclidean space of lower dimension. The flats in two-dimensional space are points and lines, and the flats in three-dimensional space are points, lines, and planes....
subset with dimension n − 1. By its nature, it separates the space into two half spaces.
Technical description
In geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hyperplane of an n-dimensional space V is a "flat" subset of dimension n − 1, or equivalently, of codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
1 in V; it may therefore be referred to as an (n − 1)-flat
Flat (geometry)
In geometry, a flat is a subset of n-dimensional space that is congruent to a Euclidean space of lower dimension. The flats in two-dimensional space are points and lines, and the flats in three-dimensional space are points, lines, and planes....
of V. The space V may be a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or more generally an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, or a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
or a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, and the notion of hyperplane varies correspondingly; in all cases however, any hyperplane can be given in coordinates as the solution of a single (due to the "codimension 1" constraint) algebraic equation of degree 1 (due to the "flat" constraint). If V is a vector space, one distinguishes "vector hyperplanes" (which are subspaces, and therefore must pass through the origin) and "affine hyperplanes" (which need not pass through the origin; they can be obtained by translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
of a vector hyperplane). A hyperplane in a Euclidean space separates that space into two half spaces, and defines a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
that fixes the hyperplane and interchanges those two half spaces.
Dihedral angles
The dihedral angleDihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
between two non-parallel hyperplanes of a Euclidean space is the angle between the corresponding normal vectors. The product of the reflections in the two hyperplanes is a rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
whose axis is the subspace of codimension 2 obtained by intersecting the hyperplanes, and whose angle is twice the angle between the hyperplanes.
Special types of hyperplanes
Several specific types of hyperplanes are defined with properties that are well suited for particular purposes. Some of these specializations are described here.Affine hyperplanes
An affine hyperplane is an affine subspaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
of codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
1 in an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
.
In Cartesian coordinates, such a hyperplane can be described with a single linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
of the following form (where at least one of the
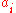 's is non-zero):
's is non-zero):
In the case of a real affine space, in other words when the coordinates are real numbers, this affine space separates the space into two half-spaces, which are the connected components of the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the hyperplane, and are given by the inequalities
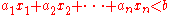
and

As an example, a line is a hyperplane in 2-dimensional space, and a plane is a hyperplane in 3-dimensional space. A line in 3-dimensional space is not a hyperplane, and does not separate the space into two parts (the complement of such a line is connected).
Any hyperplane of a Euclidean space has exactly two unit normal vectors.
Affine hyperplanes are used to define decision boundaries in many machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
algorithms such as linear-combination (oblique) decision trees
Decision tree learning
Decision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees...
, and Perceptron
Perceptron
The perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
s.
Vector hyperplanes
In a vector space, a vector hyperplane is a linear subspace of codimension 1. Such a hyperplane is the solution of a single homogeneous linear equation.Projective hyperplanes
Projective hyperplanes, are used in projective geometry. Projective geometry can be viewed as affine geometry with vanishing pointVanishing point
A vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used...
s (points at infinity) added. An affine hyperplane together with the associated points at infinity forms a projective hyperplane. One special case of a projective hyperplane is the infinite or ideal hyperplane, which is defined with the set of all points at infinity.
In real projective space, a hyperplane does not divide the space into two parts; rather, it takes two hyperplanes to separate points and divide up the space. The reason for this is that in real projective space, the space essentially "wraps around" so that both sides of a lone hyperplane are connected to each other.
See also
- hypersurfaceHypersurfaceIn geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
- decision boundaryDecision boundaryIn a statistical-classification problem with two classes, a decision boundary or decision surface is a hypersurface that partitions the underlying vector space into two sets, one for each class...
- ham sandwich theoremHam sandwich theoremIn measure theory, a branch of mathematics, the ham sandwich theorem, also called the Stone–Tukey theorem after Arthur H. Stone and John Tukey, states that given measurable "objects" in -dimensional space, it is possible to divide all of them in half with a single -dimensional hyperplane...
- arrangement of hyperplanesArrangement of hyperplanesIn geometry and combinatorics, an arrangement of hyperplanes is a finite set A of hyperplanes in a linear, affine, or projective space S....
- separating hyperplane theorem
- supporting hyperplane theorem

