
Schwarz triangle
Encyclopedia
In geometry
, a Schwarz triangle, named after Hermann Schwarz
is a spherical triangle that can be used to tile
a sphere
, possibly overlapping, through reflections in its edges. They were classified in .
These can be defined more generally as tessellations of the sphere, the Euclidean plane, or the hyperbolic plane. Each Schwarz triangle on a sphere defines a finite group
, while on the Euclidean or hyperbolic plane they define an infinite group.
A Schwarz triangle is represented by three rational numbers (p q r) each representing the angle at a vertex. The value n/d means the vertex angle is d/n of the half-circle. "2" means a right triangle. In case these are whole numbers, the triangle is called a Möbius triangle, and corresponds to a non-overlapping tiling, and the symmetry group is called a triangle group
. In the sphere there are 3 Möbius triangles plus 1 1-parameter family; in the plane there are 3 Möbius triangles, while in hyperbolic space there is a 3-parameter family of Möbius triangles, and no exceptional object
s.
. Each node represents an edge (mirror) of the Schwarz triangle. Each edge is labeled by a rational value corresponding to the reflection order, being π/vertex angle
.
Order 2 edges represents perpendicular mirrors which can be ignored in this diagram. The Coxeter-Dynkin diagram
represents this triangular graph with order-2 edges hidden.
A Coxeter group
can be used for a simpler notation, as (p q r) for cyclic graphs, and (p q 2) = [p,q] for (right triangles), and (p 2 2) = [p]×[].
Schwarz triangles with whole numbers, also called Möbius triangles, include one 1-parameter family and three exceptional
cases:
:
Density 1:
Rational solutions by density:
Density 1:
The (2 3 7) Schwarz triangle is the smallest hyperbolic Schwarz triangle, and as such is of particular interest. Its triangle group (or more precisely the index 2 von Dyck group of orientation-preserving isometries) is the (2,3,7) triangle group
, which is the universal group for all Hurwitz groups – maximal groups of isometries of Riemann surface
s. All Hurwitz groups are quotients of the (2,3,7) triangle group, and all Hurwitz surfaces are tiled by the (2,3,7) Schwarz triangle. The smallest Hurwitz group is the simple group of order 168, the second smallest non-abelian simple group
, which is isomorphic to PSL(2,7)
, and the associated Hurwitz surface (of genus 3) is the Klein quartic
.
The (2 3 8) triangle tiles the Bolza surface
, a highly symmetric (but not Hurwitz) surface of genus 2.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Schwarz triangle, named after Hermann Schwarz
Hermann Schwarz
Karl Hermann Amandus Schwarz was a German mathematician, known for his work in complex analysis. He was born in Hermsdorf, Silesia and died in Berlin...
is a spherical triangle that can be used to tile
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, possibly overlapping, through reflections in its edges. They were classified in .
These can be defined more generally as tessellations of the sphere, the Euclidean plane, or the hyperbolic plane. Each Schwarz triangle on a sphere defines a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, while on the Euclidean or hyperbolic plane they define an infinite group.
A Schwarz triangle is represented by three rational numbers (p q r) each representing the angle at a vertex. The value n/d means the vertex angle is d/n of the half-circle. "2" means a right triangle. In case these are whole numbers, the triangle is called a Möbius triangle, and corresponds to a non-overlapping tiling, and the symmetry group is called a triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
. In the sphere there are 3 Möbius triangles plus 1 1-parameter family; in the plane there are 3 Möbius triangles, while in hyperbolic space there is a 3-parameter family of Möbius triangles, and no exceptional object
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
s.
Solution space
A fundamental domain triangle, (p q r), can exist in different space depending on this constraint:-
 : Spherical
: Spherical -
 : Euclidean plane
: Euclidean plane -
 : Hyperbolic plane
: Hyperbolic plane
Graphical representation
A Schwarz triangle is represented graphically by a triangular graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. Each node represents an edge (mirror) of the Schwarz triangle. Each edge is labeled by a rational value corresponding to the reflection order, being π/vertex angle
Vertex angle
In geometry, a vertex angle is the angle associated with a vertex of a polygon.The vertex angle in a polygon is measured by the interior side of the vertex. For any simple n-gon, the sum of the interior angles is π radians or 180 degrees....
.
Schwarz triangle (p q r) on sphere |
Schwarz triangle graph |
Order 2 edges represents perpendicular mirrors which can be ignored in this diagram. The Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
represents this triangular graph with order-2 edges hidden.
A Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
can be used for a simpler notation, as (p q r) for cyclic graphs, and (p q 2) = [p,q] for (right triangles), and (p 2 2) = [p]×[].
Möbius triangles for the sphere
 (2 2 2) or [2,2] |
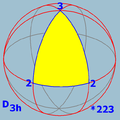 (3 2 2) or [3,2] |
... |
|---|---|---|
 (3 3 2) or [3,3] |
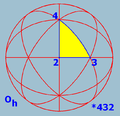 (4 3 2) or [4,3] |
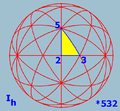 (5 3 2) or [5,3] |
Schwarz triangles with whole numbers, also called Möbius triangles, include one 1-parameter family and three exceptional
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
cases:
- [p,2] or (p 2 2) - Dihedral symmetry,
- [3,3] or (3 3 2) - Tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
, - [4,3] or (4 3 2) - Octahedral symmetryOctahedral symmetry150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
, - [5,3] or (5 3 2) - Icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
,
Schwarz triangles for the sphere by density
The Schwarz triangles (p q r), grouped by densityPolytope density
In geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...
:
| Density | Schwarz triangle |
|---|---|
| 1 | (2 3 3), (2 3 4), (2 3 5), (2 2 n) |
| d | (2 2 n/d) |
| 2 | (3/2 3 3), (3/2 4 4), (3/2 5 5), (5/2 3 3) |
| 3 | (2 3/2 3), (2 5/2 5) |
| 4 | (3 4/3 4), (3 5/3 5) |
| 5 | (2 3/2 3/2), (2 3/2 4) |
| 6 | (3/2 3/2 3/2), (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5) |
| 7 | (2 3 4/3), (2 3 5/2) |
| 8 | (3/2 5/2 5) |
| 9 | (2 5/3 5) |
| 10 | (3 5/3 5/2), (3 5/4 5) |
| 11 | (2 3/2 4/3), (2 3/2 5) |
| 13 | (2 3 5/3) |
| 14 | (3/2 4/3 4/3), (3/2 5/2 5/2), (3 3 5/4) |
| 16 | (3 5/4 5/2) |
| 17 | (2 3/2 5/2) |
| 18 | (3/2 3 5/3), (5/3 5/3 5/2) |
| 19 | (2 3 5/4) |
| 21 | (2 5/4 5/2) |
| 22 | (3/2 3/2 5/2) |
| 23 | (2 3/2 5/3) |
| 26 | (3/2 5/3 5/3) |
| 27 | (2 5/4 5/3) |
| 29 | (2 3/2 5/4) |
| 32 | (3/2 5/45/3) |
| 34 | (3/2 3/2 5/4) |
| 38 | (3/2 5/4 5/4) |
| 42 | (5/4 5/4 5/4) |
Triangles for the Euclidean plane
 (3 3 3) |
 (4 4 2) |
 (6 3 2) |
Density 1:
- (3 3 3) – 60-60-60 (equilateral)
- (4 4 2) – 45-45-90 (isosceles right)
- (6 3 2) – 30-60-90
Rational solutions by density:
- Density 0: (4 4/3 ∞), (3 3/2 ∞), (6 6/5 ∞)
- Density 1: (4/3 4/3 2), (4/3 4 2), (6 3/2 2)
- Density 2: (6/5 3 2), (6 6 3/2), (6 6/5 3)
Triangles for the hyperbolic plane
 (7 3 2) |
 (8 3 2) |
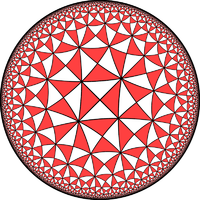 (5 4 2) |
 (4 3 3) |
 (4 4 3) |
(∞ ∞ ∞) |
| Fundamental domains of (p q r) triangles | ||
Density 1:
- (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
- (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
- (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
- (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
- (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
- (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
- (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
- (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
- ...
- (∞ ∞ ∞)
The (2 3 7) Schwarz triangle is the smallest hyperbolic Schwarz triangle, and as such is of particular interest. Its triangle group (or more precisely the index 2 von Dyck group of orientation-preserving isometries) is the (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
, which is the universal group for all Hurwitz groups – maximal groups of isometries of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s. All Hurwitz groups are quotients of the (2,3,7) triangle group, and all Hurwitz surfaces are tiled by the (2,3,7) Schwarz triangle. The smallest Hurwitz group is the simple group of order 168, the second smallest non-abelian simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, which is isomorphic to PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
, and the associated Hurwitz surface (of genus 3) is the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
.
The (2 3 8) triangle tiles the Bolza surface
Bolza surface
In mathematics, the Bolza surface, alternatively, complex algebraic Bolza curve , is a compact Riemann surface of genus 2 with the highest possible order of the conformal automorphism group in this genus, namely 48. An affine model for the Bolza surface can be obtained as the locus of the...
, a highly symmetric (but not Hurwitz) surface of genus 2.
See also
- Wythoff symbolWythoff symbolIn geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
- Wythoff constructionWythoff constructionIn geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
- Uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
- Nonconvex uniform polyhedronNonconvex uniform polyhedronIn geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
- Polytope densityPolytope densityIn geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...
- Goursat tetrahedronGoursat tetrahedronIn geometry, a Goursat tetrahedron is a tetrahedral fundamental domain of a Wythoff construction. Each tetrahedral face represents a reflection hyperplane on 3-dimensional surfaces: the 3-sphere, the Euclidean 3-space, and hyperbolic 3-space. Coxeter named after Edouard Goursat who first looked...
- Regular hyperbolic tiling
- Uniform tilings in hyperbolic planeUniform tilings in hyperbolic planeThere are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...

