
Perpendicular
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, two lines
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
or planes (or a line and a plane) are considered perpendicular (or orthogonal) to each other if they form congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
adjacent
Adjacent angles
In geometry, adjacent angles, often shortened as adj. ∠s, are angles that have a common ray coming out of the vertex going between two other rays. In other words, they are angles that are side by side, or adjacent.- Complementary adjacent angles :...
angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s (a T-shape). The term may be used as a noun
Noun
In linguistics, a noun is a member of a large, open lexical category whose members can occur as the main word in the subject of a clause, the object of a verb, or the object of a preposition .Lexical categories are defined in terms of how their members combine with other kinds of...
or adjective
Adjective
In grammar, an adjective is a 'describing' word; the main syntactic role of which is to qualify a noun or noun phrase, giving more information about the object signified....
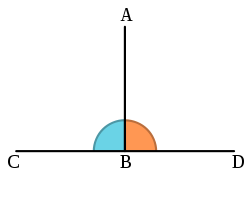
. Thus, as illustrated, the line AB is the perpendicular to CD through the point A.
By definition, a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
is infinitely long, and strictly speaking AB and CD in this example represent line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s of two infinitely long lines. Hence the line segment AB does not have to intersect line segment CD to be considered perpendicular lines, because if the line segments are extended out to infinity, they would still form congruent adjacent angles.
If a line is perpendicular to another as shown, all of the angles created by their intersection are called right angles (right angles measure π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
/2 radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, or 90°
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
). Conversely, any lines that meet to form right angles are perpendicular.
In a coordinate plane, perpendicular lines have opposite reciprocal slopes. A horizontal line has slope equal to zero while the slope of a vertical line is described as undefined or sometimes ±infinity. Two lines that are perpendicular would be denoted as AB
 CD.
CD.Construction of the perpendicular
To make the perpendicular to the line AB through the point P using compass and straightedgeCompass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, proceed as follows (see figure):
- Step 1 (red): construct a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with center at P to create points A' and B' on the line AB, which are equidistantEquidistantA point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.In two-dimensional Euclidian geometry the locus of points equidistant from two given points is their perpendicular bisector...
from P. - Step 2 (green): construct circles centered at A' and B', both passing through P. Let Q be the other point of intersection of these two circles.
- Step 3 (blue): connect P and Q to construct the desired perpendicular PQ.
To prove that the PQ is perpendicular to AB, use the SSS congruence theorem for ' and QPB' to conclude that angles OPA' and OPB' are equal. Then use the SAS congruence theorem for triangles OPA' and OPB' to conclude that angles POA and POB are equal.
In relationship to parallel lines
If two lines (a and b) are both perpendicular to a third line (c), all of the angles formed along the third line are right angles. Therefore, in Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, any two lines that are both perpendicular to a third line are parallel to each other, because of the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
. Conversely, if one line is perpendicular to a second line, it is also perpendicular to any line parallel to that second line.
In the figure at the right, all of the orange-shaded angles are congruent to each other and all of the green-shaded angles are congruent to each other, because vertical angles
Vertical (angles)
In geometry, a pair of angles is said to be vertical if the angles are formed from two intersecting lines and the angles are not adjacent. The two angles share a vertex...
are congruent and alternate interior angles formed by a transversal cutting parallel lines are congruent. Therefore, if lines a and b are parallel, any of the following conclusions leads to all of the others:
- One of the angles in the diagram is a right angle.
- One of the orange-shaded angles is congruent to one of the green-shaded angles.
- Line 'c' is perpendicular to line 'a'.
- Line 'c' is perpendicular to line 'b'.
Perpendicular symbol
The perpendicular symbol is . For example,
. For example,  indicates that line AB is perpendicular to line CD.
indicates that line AB is perpendicular to line CD.In the Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
character set, the perpendicular sign has the codepoint U+27C2 and is part of the Miscellaneous Mathematical Symbols-A range. It looks similar to the up tack symbol (U+22A5).
See also
- OrthogonalityOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
- Perpendicular component (of a vector)
- Surface normalSurface normalA surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
- Parallel (geometry)Parallel (geometry)Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
External links
- Definition: perpendicular With interactive animation
- How to draw a perpendicular bisector of a line with compass and straight edge Animated demonstration
- How to draw a perpendicular at the endpoint of a ray with compass and straight edge Animated demonstration

