Fundamental domain
Encyclopedia
In geometry
, the fundamental domain of a symmetry group
of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry
. More rigorously, given a topological space
and a group
acting
on it, the images of a single point under the group action form an orbit of the action. A fundamental domain is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits.
There are many ways to choose a fundamental domain. Typically, a fundamental domain is required to be a connected
subset with some restrictions on its boundary, for example, smooth or polyhedral. The images of a chosen fundamental domain under the group action then tile
the space. One general construction of fundamental domains uses Voronoi cells.
G on a topological space
X by homeomorphism
s, a fundamental domain (also called fundamental region) for this action is a set D of representatives for the orbits. It is usually required to be a reasonably nice set topologically, in one of several precisely defined ways. One typical condition is that D is almost an open set, in the sense that D is the symmetric difference
of an open set in G with a set of measure zero, for a certain (quasi)invariant measure
on X. A fundamental domain always contains a free regular set
U, an open set
moved around by G into disjoint copies, and nearly as good as D in representing the orbits. Frequently D is required to be a complete set of coset representatives with some repetitions, but the repeated part has measure zero. This is a typical situation in ergodic theory
. If a fundamental domain is used to calculate an integral
on X/G, sets of measure zero do not matter.
For example, when X is Euclidean space
Rn of dimension n, and G is the lattice Zn acting on it by translations, the quotient X/G is the n-dimensional torus
. A fundamental domain D here can be taken to be[0,1) n, which differs from the open set (0,1)n by a set of measure zero, or the closed
unit cube[0,1] n, whose boundary
consists of the points whose orbit has more than one representative in D.
In the case of translational symmetry combined with other symmetries, the fundamental domain is part of the primitive cell. For example, for wallpaper group
s the fundamental domain is a factor 1, 2, 3, 4, 6, 8, or 12 smaller than the primitive cell.
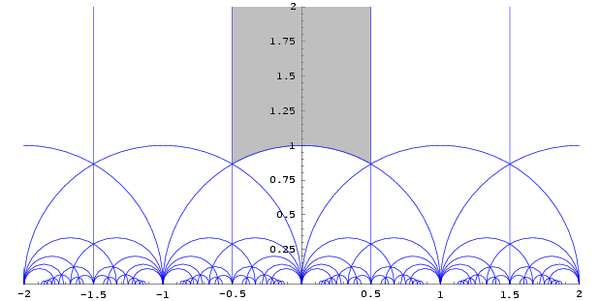The existence and description of a fundamental domain is in general something requiring painstaking work to establish. The diagram to the right shows part of the construction of the fundamental domain for the action of the modular group
Γ on the upper half-plane H.
This famous diagram appears in all classical books on modular functions. (It was probably well known to C. F. Gauss, who dealt with fundamental domains in the guise of the reduction theory of quadratic forms.) Here, each triangular region (bounded by the blue lines) is a free regular set
of the action of Γ on H. The boundaries (the blue lines) are not a part of the free regular sets. To construct a fundamental domain of H/Γ, one must also consider how to assign points on the boundary, being careful not to double-count such points. Thus, the free regular set in this example is
The fundamental domain is built by adding the boundary on the left plus half the arc on the bottom including the point in the middle:
The choice of which points of the boundary to include as a part of the fundamental domain is arbitrary, and varies from author to author.
The core difficulty of defining the fundamental domain lies not so much with the definition of the set per se, but rather with how to treat integrals over the fundamental domain, when integrating functions with poles and zeros on the boundary of the domain.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the fundamental domain of a symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. More rigorously, given a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on it, the images of a single point under the group action form an orbit of the action. A fundamental domain is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits.
There are many ways to choose a fundamental domain. Typically, a fundamental domain is required to be a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
subset with some restrictions on its boundary, for example, smooth or polyhedral. The images of a chosen fundamental domain under the group action then tile
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
the space. One general construction of fundamental domains uses Voronoi cells.
Hints at general definition
Given an action of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X by homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s, a fundamental domain (also called fundamental region) for this action is a set D of representatives for the orbits. It is usually required to be a reasonably nice set topologically, in one of several precisely defined ways. One typical condition is that D is almost an open set, in the sense that D is the symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
of an open set in G with a set of measure zero, for a certain (quasi)invariant measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on X. A fundamental domain always contains a free regular set
Free regular set
In mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X...
U, an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
moved around by G into disjoint copies, and nearly as good as D in representing the orbits. Frequently D is required to be a complete set of coset representatives with some repetitions, but the repeated part has measure zero. This is a typical situation in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
. If a fundamental domain is used to calculate an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
on X/G, sets of measure zero do not matter.
For example, when X is Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn of dimension n, and G is the lattice Zn acting on it by translations, the quotient X/G is the n-dimensional torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. A fundamental domain D here can be taken to be
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
unit cube
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
consists of the points whose orbit has more than one representative in D.
Examples
Examples in the three-dimensional Euclidean space R3.- for n-fold rotation: an orbit is either a set of n points around the axis, or a single point on the axis; the fundamental domain is a sector
- for reflection in a plane: an orbit is either a set of 2 points, one on each side of the plane, or a single point in the plane; the fundamental domain is a half-space bounded by that plane
- for inversion in a point: an orbit is a set of 2 points, one on each side of the center, except for one orbit, consisting of the center only; the fundamental domain is a half-space bounded by any plane through the center
- for 180° rotation about a line: an orbit is either a set of 2 points opposite to each other with respect to the axis, or a single point on the axis; the fundamental domain is a half-space bounded by any plane through the line
- for discrete translational symmetryTranslational symmetryIn geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
in one direction: the orbits are translates of a 1D lattice in the direction of the translation vector; the fundamental domain is an infinite slab - for discrete translational symmetry in two directions: the orbits are translates of a 2D lattice in the plane through the translation vectors; the fundamental domain is an infinite bar with parallelogramParallelogramIn Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
matic cross section - for discrete translational symmetry in three directions: the orbits are translates of the lattice; the fundamental domain is a primitive cellPrimitive cellUsed predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
which is e.g. a parallelepipedParallelepipedIn geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
, or a Wigner-Seitz cellWigner-Seitz cellThe Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a type of Voronoi cell used in the study of crystalline material in solid-state physics....
, also called Voronoi cellVoronoi diagramIn mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
/diagram.
In the case of translational symmetry combined with other symmetries, the fundamental domain is part of the primitive cell. For example, for wallpaper group
Wallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s the fundamental domain is a factor 1, 2, 3, 4, 6, 8, or 12 smaller than the primitive cell.
Fundamental domain for the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
Γ on the upper half-plane H.
This famous diagram appears in all classical books on modular functions. (It was probably well known to C. F. Gauss, who dealt with fundamental domains in the guise of the reduction theory of quadratic forms.) Here, each triangular region (bounded by the blue lines) is a free regular set
Free regular set
In mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X...
of the action of Γ on H. The boundaries (the blue lines) are not a part of the free regular sets. To construct a fundamental domain of H/Γ, one must also consider how to assign points on the boundary, being careful not to double-count such points. Thus, the free regular set in this example is
The fundamental domain is built by adding the boundary on the left plus half the arc on the bottom including the point in the middle:
The choice of which points of the boundary to include as a part of the fundamental domain is arbitrary, and varies from author to author.
The core difficulty of defining the fundamental domain lies not so much with the definition of the set per se, but rather with how to treat integrals over the fundamental domain, when integrating functions with poles and zeros on the boundary of the domain.
See also
- Free regular setFree regular setIn mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X...
- Fundamental polygonFundamental polygonIn mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....
- Brillouin zoneBrillouin zoneIn mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
- Fundamental pair of periodsFundamental pair of periodsIn mathematics, a fundamental pair of periods is an ordered pair of complex numbers that define a lattice in the complex plane. This type of lattice is the underlying object with which elliptic functions and modular forms are defined....
- Petersson inner product
- Cusp neighborhoodCusp neighborhoodIn mathematics, a cusp neighborhood is defined as a set of points near a cusp.-Cusp neighborhood for a Riemann surface:The cusp neighborhood for a hyperbolic Riemann surface can be defined in terms of its Fuchsian model....